7. úloha vzorové riešenie

Na začiatok si musíme ujasniť, čo je cieľom úlohy. Máme daný nejaký trojuholník \(ABC\) a v ňom niekoľko bodov. Avšak nie je to hocijaký trojuholník. Zadanie nám hovorí, že bod \(X\) má ležať na osi úsečky \(PQ\). Isto ste si všimli, že to neplatí v každom trojuholníku. Taktiež je ľahké si rozmyslieť, že ak trojuholník \(ABC\) bude rovnoramenný so základňou \(BC\), tak bod \(X\) na osi \(PQ\) naozaj bude ležať. O tomto však úloha nie je. My máme dokázať, že ak si narysujeme nejaký trojuholník \(ABC\), v ktorom bude bod \(X\) ležať na osi úsečky \(PQ\), tak ten trojuholník musí byť rovnoramenný. Je dobré, aby sme si nakreslili trojuholník, ktorý nie je rovnoramenný, aby nás náčrt zbytočne nezvádzal používať tvrdenia, ktoré sme nedokázali.

Čo vieme z toho, že bod \(X\) leží na osi úsečky \(PQ\)? Vieme, že je rovnako vzdialený od jej krajných bodov, teda \(|PX| = |QX|\). Tak poďme hľadať nejaké vzťahy medzi dĺžkami strán a pokúsime sa dopracovať k tomu, že \(|AB| = |AC|\).

Začneme s niekoľkými počiatočnými pozorovaniami. Trojuholníky \(BZI\) a \(BXI\) sú zhodné podľa vety sus (rozmyslite si to). Z rovnakého dôvodu platia aj zhodnosti \(\triangle CXI \cong \triangle CYI\) a \(\triangle AYI \cong \triangle AZI\). Môžeme teda povedať, že \(|BX| = |BZ|\), \(|CX| = |CY|\) a \(|AY| = |AZ|\). Trojuholník \(AZY\) je rovnoramenný. Priamka \(AI\) je v ňom osou uhla pri vrchole \(A\), a preto je zároveň aj osou úsečky \(YZ\). Podobne, priamky \(BI\) a \(CI\) sú osami úsečiek \(ZX\) a \(XY\). Tieto pozorovania je dobré mať na pamäti, keď sa v úlohe objaví vpísaná kružnica a jej body dotyku so stranami.

Keď už vieme toto, môžeme si všimnúť zhodné trojuholníky \(BXP\) a \(BZP\), teraz podľa vety sus. Z tejto podobnosti dostaneme už zaujímavejšiu rovnosť \(|PZ| = |PX|\). Analogicky zo zhodných trojuholníkov \(CXQ\) a \(CYQ\) dostaneme, že \(|QY| = |QX|\). Teraz môžeme využiť náš poznatok o tom, že \(|PX| = |QX|\). Spojením týchto rovností dostaneme \(|PZ| = |PX| = |QX| = |QY|\).

Označme si \(S\) stred úsečky \(PQ\). Ak sa pozrieme na náš obrázok [fig:7-1], všimneme si, že patí \(|ZP| = |ZS| + |SP|\), \(|QY| = |QS| + |SY|\) a ako sme vyššie ukázali, tak \(|ZP| = |QY|\). Po rozpísaní teda dostaneme \(|ZS| + |SP| =\) \(= |QS| + |SY|\). Ak využijeme, že \(|QS| = |SP|\), tak máme rovnosť \(|ZS| = |SY|\). Tá nám hovorí, že bod \(S\) je zároveň aj stredom úsečky \(ZY\).

[c]0.5 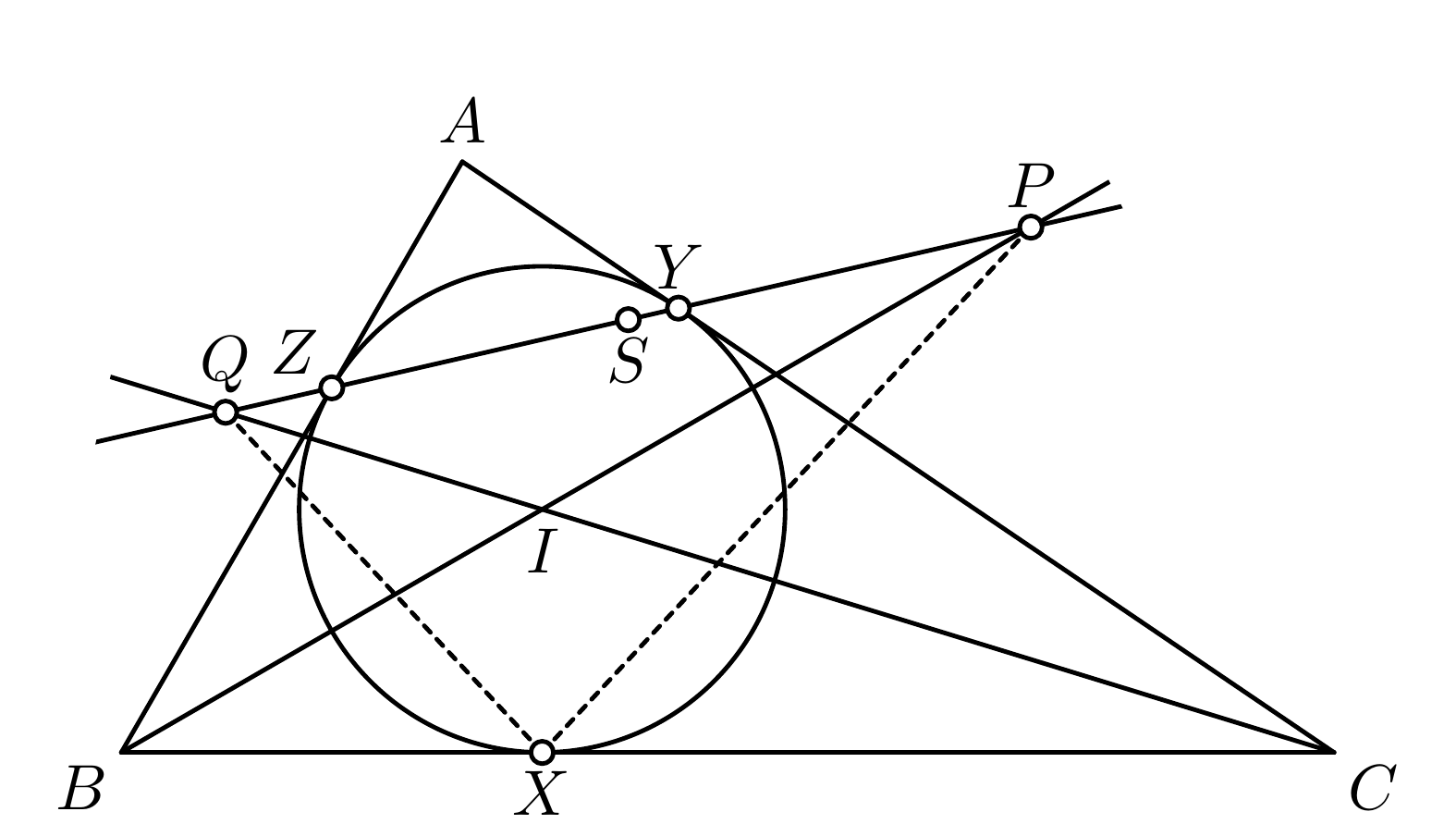[fig:7-1]

[c]0.45 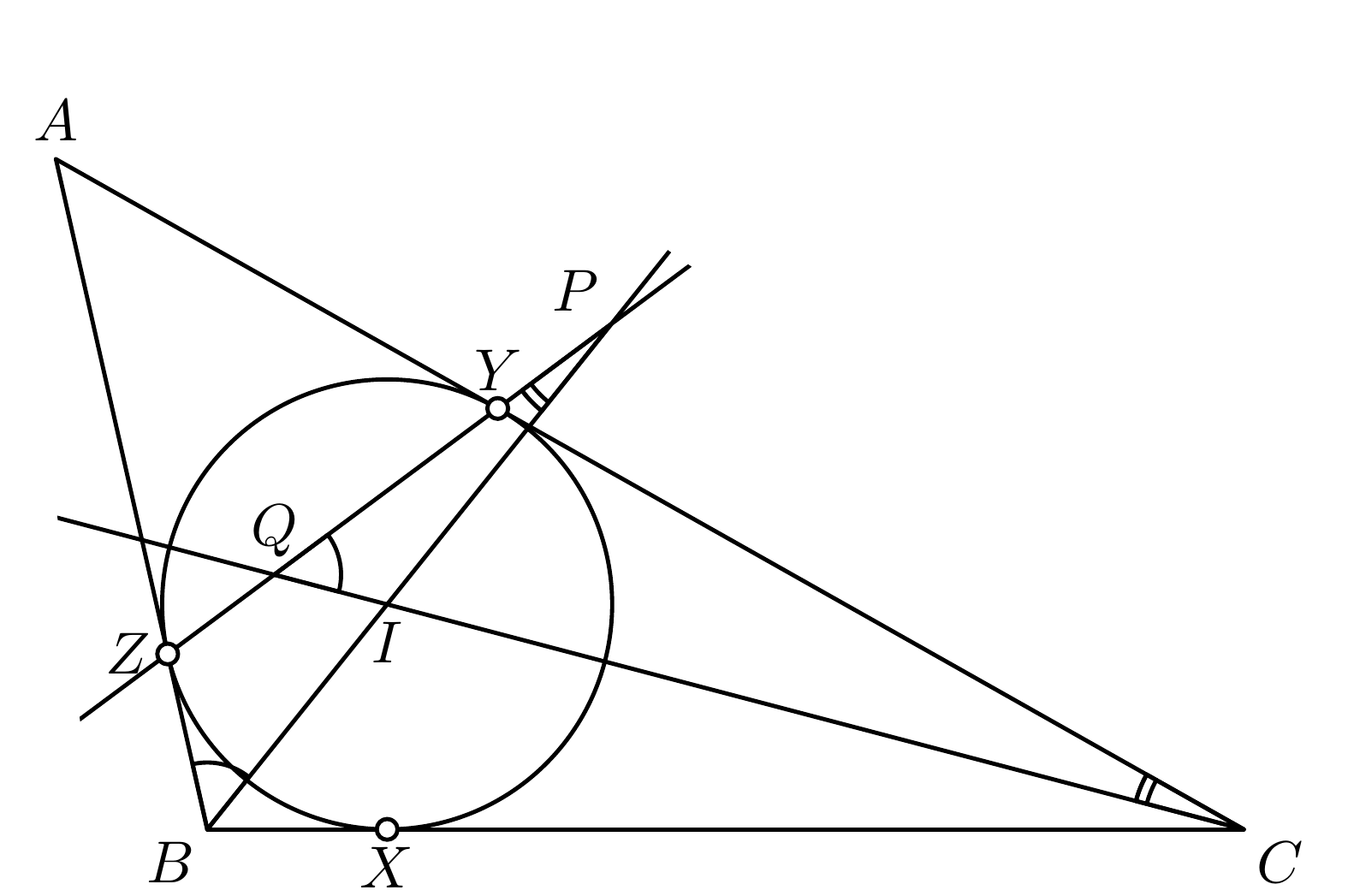[fig:7-2]

To nám nahráva do kariet, lebo ako sme vyššie ukázali, priamka \(AI\) je osou úsečky \(ZY\). Priamka \(SX\) je tiež kolmá na úsečku \(ZY\) a prechádza jej stredom, teda je tiež jej osou. To znamená, že os úsečky \(PQ\) a priamka \(AI\) splývajú. Inými slovami, body \(A\), \(S\), \(I\), \(X\) ležia na jednej priamke. Avšak uhol \(IXB\) je pravý, lebo dotyčnica \(BC\) je kolmá na polomer \(IX\) vpísanej kružnice. Dostali sme teda, že os uhla \(BAC\) je kolmá na stranu \(BC\). Z toho už ľahko vyplýva, že trojuholník \(ABC\) je rovnoramenný.

Sme teda spokojní, lebo sme dokázali, čo sme mali. Zabudli sme však na jednu vec. Pri dokazovaní, že \(S\) je stred úsečky \(YZ\) sme využívali, že body \(Z\), \(Q\), \(S\), \(P\), \(Y\) ležia na priamke v uvedenom poradí. Tieto body však vo všeobecnom¹ trojuholníku \(ABC\) môžu ležať aj niekoľkých iných poradiach (aj napr. \(Q\), \(S\), \(Z\), \(Y\), \(P\), kedy neplatí \(|ZP| = |ZS| + |SP|\)). Tieto poradia budeme vždy udávať v smere od \(Y\) ku \(Z\). Ako sa riešenie úlohy zmení a ktoré pozície vlastne môžu nastať?

Stačí nám ukázať, že platia rovnosti \(|ZP| = |ZS| + |SP|\), resp. \(|QY| = |QS| + |SY|\). Tie využívajú poradie bodov \(Z\), \(S\), \(P\), resp. \(Q\), \(S\), \(Y\). Očividne body \(P\), \(S\), \(Q\) ležia na priamke \(YZ\) v tomto poradí. Čo by sa stalo, ak by bod \(S\) ležal pred bodom \(Z\)? Potom by \(|PZ| < |SP|\) a \(|QY| > |QS| = |SP|\), teda úsečky \(ZP\) a \(QY\) nemôžu byť rovnako dlhé, čo je spor, lebo sme ukázali rovnosť ich dĺžok. Preto body \(Z\), \(S\), \(Q\) vždy ležia na priamke \(ZY\) v tomto poradí. Analogicky to platí aj pre body \(Q\), \(S\), \(Y\). Môže sa nám ešte stať, že nejaké body splynú v jeden, vtedy budeme mať nulovú vzdialenosť, ale to nám rovnosti nepokazí. Rovnosti \(|ZP| = |ZS| + |SP|\) a \(|QY| = |QS| + |SY|\) teda platia vždy a z nich vieme už ukázať, že bod \(S\) je stredom úsečky \(YZ\).

Ak si prejdeme naše zvyšné úvahy, tak žiadne ďalšie už nevyužívajú nejakú špeciálnu polohu bodov. Ukázali sme teda, že pri ľubovoľnom možnom rozmiestnení bodov, musí byť trojuholník \(ABC\) rovnoramenný.

Stručne si naznačíme ešte jedno riešenie. Namiesto dĺžok strán budeme pracovať s uhlami. Budeme používať štandardné označenie veľkostí uhlov v trojuholníku. Trojuholník \(AZY\) je rovnoramenný preto \(|\sphericalangle AYZ| = 90\st - \alpha/2\) a \(|\sphericalangle ZYC| = 90\st + \alpha/2\). V trojuholníku \(CYQ\) potom vieme dopočítať \(|\sphericalangle PQC| = 180\st - (90\st + \alpha/2) - \gamma/2 = \beta/2\). Uhly \(PQC\) a \(PBZ\) majú rovnakú veľkosť, preto body \(B\), \(I\), \(Z\), \(O\) ležia na kružnici. Avšak podobne, ako v prvom riešení, aj tu si musíme dať pozor na polohu bodov. Od nej závisí dôvod, prečo je štvoruholník \(BIZQ\) tetivový.

• Ak je bod \(Q\) vnútri trojuholníka \(ABC\), tak je to rovnosť \(|\sphericalangle IBZ| + |\sphericalangle IQZ| = 180\st\).

• Ak je bod \(Q\) mimo trojuholníka \(ABC\), tak je to rovnosť obvodových uholov \(IBZ\) a \(IQZ\).

• Ak bod \(Q\) leží na strane \(AB\), t. j. v bode \(Y\), tak ide o tri body, ktoré na kružnici ležia vždy.

Prvé dva prípady môžete nájsť na obrázku [fig:7-2]. Štvor(troj)uholník \(BIZQ\) je teda vždy tetivový a preto \(|\sphericalangle BQC| =\) \(= |\sphericalangle BZI| = 90\st\). Analogicky na druhej strane dopočítame \(|\sphericalangle BPC| = 90\st\). Z toho vyplýva, že body \(B\), \(C\), \(P\), \(Q\) ležia na tálesovej kružnici nad priemerom \(BC\). Teraz si len stačí uvedomiť, že os úsečky \(PQ\) prechádza stredom tálesovej kružnice – stredom strany \(BC\). Keďže os \(PQ\) pretína stranu \(BC\) v bode \(X\), tak \(X\) musí byť stred strany \(BC\). Ak sa má kružnica vpísaná trojuholníku \(ABC\) dotýkať strany \(BC\) v strede, tak \(ABC\) musí byť rovnoramenný trojuholník.

Častou chybou pri riešení bolo nerozobratie možných polôh bodov. Tie totiž ovplyvňujú niektoré vzťahy, ktoré pri riešení používame. V prvom riešení to na ne nemalo vplyv. V druhom riešení už vždy neplatila zhodnosť uhlov \(IBZ\) a \(IQZ\). Ak by sme využívali iné uhly, tak by sme mohli nesprávne tvrdiť, že \(|\angle PYC| = |\angle AYZ|=\) \(= 90\st -\alpha/2\), lebo sú to vrcholové uhly. Pri inej polohe bodov (ak by bol P vnútri trojuholníka \(ABC\)) totiž môže ísť aj o susedné a dostaneme inú veľkosť uhla \(PYC\).

Na záver by sme vám dali do pozornosti ešte jedno riešenie tejto úlohy, v ktorom nie je dobre rozobraná poloha bodov. Dokonca toto riešenie nevyužíva ani predpoklad, že bod \(X\) leží na osi úsečky \(PQ\) a úlohu rieši všeobecne! Nájdete ho ako príklad 5 v článku https://old.kms.sk/~mazo/matematika/pocitanieUhlov.pdf.