Zadanie
Alžbetka si doniesla na ihrisko kriedy. Bielou kriedou si nakreslila na ihrisko \(n\) bodov. Potom niektoré dvojice bodov spojila bielou čiarou tak, aby sa čiary nepretínali inde, ako v nakreslených \(n\) bodoch. Nakoniec zobrala tri farebné kriedy a rozhodla sa, že každý z \(n\) bodov, čo nakreslila na začiatku, vyfarbí jednou farbou. Vyfarbuje ich však tak, aby každé dva body, ktoré sú spojené čiarou, mali rôznu farbu. Avšak za žiadnu cenu sa Alžbetke nepodarilo takto zafarbiť všetky body. Nájdite najmenšie kladné celé číslo \(n\), pre ktoré sa to mohlo Alžbetke stať. Ako napríklad mohli vyzerať body a čiary, ktoré na začiatku nakreslila? Prečo sa jej to nemohlo stať pre menšie \(n\)?
Keďže hľadáme najmenšie kladné \(n\), predstavme si situáciu pre malé kladné čísla. Pre \(n=1\) máme iba jeden bod, ktorý nemáme s čím spojiť, teda nemáme žiadne čiary. Takže neplatí, že by nejaká čiara mala oba konce rovnakej farby.
Pre \(n=2\) máme dva body, vieme ich spojiť čiarou. Môžeme však použiť 3 rôzne farby, preto stačí, ak každý zafarbíme inou farbou.
Pre \(n=3\) môžeme znovu zafarbiť každý bod inou farbou, teda aj keby sme spojili každý vrchol s každým, žiadna čiara nebude mať rovnaké konce. Čo sa však stane, ak je počet bodov väčší než počet farieb?
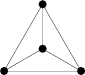
Vezmime \(n=4\) a spojme každý bod s každým tak, ako na obrázku. Museli sme sa trochu potrápiť, aby sa nám to podarilo bez kríženia čiar. Zafarbime nejaký prvý bod nejakou farbou, napr. modrou. Teraz druhý bod je spojený s každým, teda aj s prvým, preto musí mať inú farbu, povedzme, že červenú. Tretí bod je tiež spojený s oboma predchádzajúcimi, teda musí mať tretiu farbu, napríklad zelenú. Štvrtý bod je ale tiež spojený so všetkými prechádzajúcimi bodmi, takže musí mať inú farbu. Môžeme ale použiť iba 3 farby, takže štvrtý bod bude mať iste rovnakú farbu ako niektorý z predchádzajúcich, teda čiara, ktorá ich spája, má oba konce rovnakej farby. Najmenšie možné \(n\) je teda \(4\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.