Zadanie
Marián sa rozhodol, že sa začne venovať geometrii. Čarodejník Š mu poradil, že podstatou každej geometrickej úlohy je nájsť 4 body, čo ležia na jednej kružnici. Skúste to s ním aj vy!
Majme rovnobežník $ABCD$. Nech $H$ je priesečník výšok trojuholníka $ABC$. Rovnobežka so stranou $AB$ cez bod $H$ pretína priamky $AD$ a $BC$ postupne v bodoch $Q$ a $P$. Rovnobežka so stranou $BC$ cez bod $H$ pretína priamky $AB$ a $CD$ postupne v bodoch $R$ a $S$. Dokážte, že body $P$, $Q$, $R$, $S$ ležia na jednej kružnici.
To, že body \(P,\ Q,\ R,\ S\) ležia na jednej kružnici dokážeme pomocou mocnosti bodu \(H\)1. Potrebujeme dokázať vzťah \(|PH|\cdot|QH|=|RH|\cdot|SH|\). Poďme na to.
Označme si postupne päty výšok v trojuholníku \(ABC\) z bodov \(A,\ C\) ako \(X,\ Y\). Vieme, že body \(A,\ C,\ X,\ Y\) ležia na jednej kružnici – na Talesovej kružnici nad priemerom \(AC\). Z mocnosti bodu \(H\) k tejto kružnici dostávame, že platí \(|AH|\cdot|XH|=|CH|\cdot|YH|\). Potrebujeme teraz len nejakým spôsobom prejsť od tejto rovnosti k dokazovanej rovnosti.
To spravíme jednoducho. Všimnime si trojuholníky \(PXH,\ QAH,\ RYH,\ SCH\). Všetky sú pravouhlé, vďaka tomu, že \(ABCD\) je rovnobežník a \(AX\) a \(CY\) sú výšky v trojuholníku \(ABC\). Navyše vďaka rovnobežnostiam \(AB\parallel PQ\parallel CD\) a \(BC\parallel RS\parallel AD\) platí, že uhol pri vrcholoch \(P,\ Q,\ R,\ S\) v týchto trojuholníkoch je vždy uhol, ktorý zvierajú priamky \(AB\) a \(AC\). Preto sú všetky tieto trojuholníky podobné.
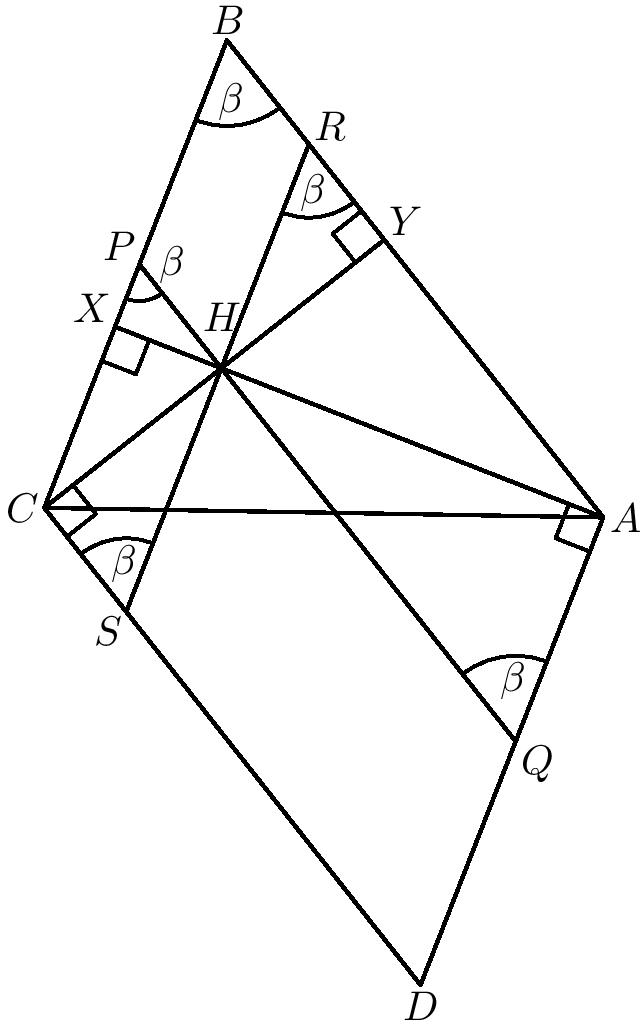
Z podobnosti týchto štyroch trojuholníkov máme, že platí: \[\frac{|PH|}{|XH|}=\frac{|QH|}{|AH|}=\frac{|RH|}{|YH|}=\frac{|SH|}{|CH|}.\]
Z tohto a rovnosti \(|AH|\cdot|XH|=|CH|\cdot|YH|\) zrejme vyplýva dokazovaná rovnosť \(|PH|\cdot|QH|=|RH|\cdot|SH|\). Preto body \(P,\ Q,\ R,\ S\) ležia na jednej kružnici.
Na záver geometrickej úlohy sa hodí urobiť diskusiu o možnej polohe bodov. Riešenie je písané tým štýlom, že ak trojuholníky \(PXH,\ QAH,\ RYH,\ SCH\) existujú, tak sa nemá čo pokaziť. Je jedno, či je \(ABC\) tupouhlý a či \(H\) leží vnútri alebo nie, všetky argumenty platia rovnako. Jediný problém môže nastať ak spomínané trojuholníky neexistujú, a to nastane keď niektoré body splynú do jedného. To sa stane, ak je trojuholník \(ABC\) pravouhlý. Nech je však pravouhlý pri hociktorom vrchole, tak si ľahko rozmyslíme, že v tom prípade dva z bodov \(P,\ Q,\ R,\ S\) splynú do jedného a dokázať, že 3 body ležia na jednej kružnici je už triviálne, lebo neležia na jednej priamke. Tým sme prebrali naozaj všetko a úloha je dokázaná.
Pokiaľ si sa s mocnosťou bodu ku kružnici, ešte nestretol, môžeš si o nej prečítať v Zbierke KMS od strany 37.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.