Zadanie
Povesť Mr. Mira sa doniesla až do zahraničia. Zavolal si ho Jaromír Jágr, aby mu pomohol s výzdobou kuchyne. Jágr má v kuchyni vykachličkovaný štvorec $n\times n$ štvorcovými kachličkami $1 \times 1$. Chce ho vyzdobiť pomocou niekoľkých pravouhlých rovnoramenných trojuholníkov s preponou dĺžky $2$, ktorých vrcholy sa budú nachádzať v mrežových bodoch štvorčekovej siete, ktorú vytvárajú kachličky. Navyše každá strana kachličky sa musí nachádzať práve v jednom trojuholníku (vnútri neho alebo na okraji). Nájdite všetky prirodzené čísla $n$, pre ktoré je to možné.
Upresnenie. Keď sa kachličky dotýkajú stranou, tak ich strany, ktoré sa dotýkajú, splývajú do jednej úsečky. Tieto strany teda nemôžu byť v dvoch rôznych trojuholníkoch.
Riešenie takejto úlohy sa bude skladať z dvoch častí. Najprv sa pokúsime orezať množinu čísel \(n\), pre ktoré sa štvorce \(n\times n\) budú dať „vytrojuholníkovať“ pomocou nejakých nutných podmienok, ktoré musí \(n\) spĺňať. Potom pomocou konkrétnej konštrukcie (indukciou, alebo rekurzívnym popísaním) ukážeme, že všetky \(n\), ktoré nám ostali, naozaj budú spĺňať podmienku zo zadania.
Začnime pozorovaním, že na celom obvode, štvorca, musia byť priložené trojuholníky preponou. Ak by na niektorej strane štvorca bol priložený trojuholník odvesnou, tak aspoň dva jeho vrcholy sa nebudú nachádzať v mrežových bodoch. Párna dĺžka prepony preto zaručuje, že \(n\) musí byť párne.
Na druhú podmienku využijeme, aký je celkový počet hrán. Zvislých hrán je \(n\) v každom z \(n+1\) stĺpcov a vodorovných je rovnako veľa. Dokopy máme \(2n(n+1)\) hrán. Každý z umiestnených trojuholníkov pokryje tri takéto hrany (dve preponou a jednu výškou na preponu). Preto číslo \(2n(n+1)\) musí byť deliteľné tromi, teda \(n\) dáva zvyšok \(0\) alebo \(2\) po delení tromi.
Spojením týchto dvoch podmienok dostávame, že \(n\) dáva jeden zo zvyškov \(\{0,2\}\) po delení šiestimi (pri ostatných zvyškoch nie je splnená jedna z podmienok).
Prestúpme do druhej časti riešenia a skúsme nájsť postup, podľa ktorého budeme „trojuholníkovať“ štvorce takýchto veľkostí. Ako rozumná možnosť sa ponúka vymyslieť nejaký spôsob pre malé čísla – \(2\), \(6\) a potom navrhnúť spôsob ako stranu týchto riešení zväčšovať o \(6\).
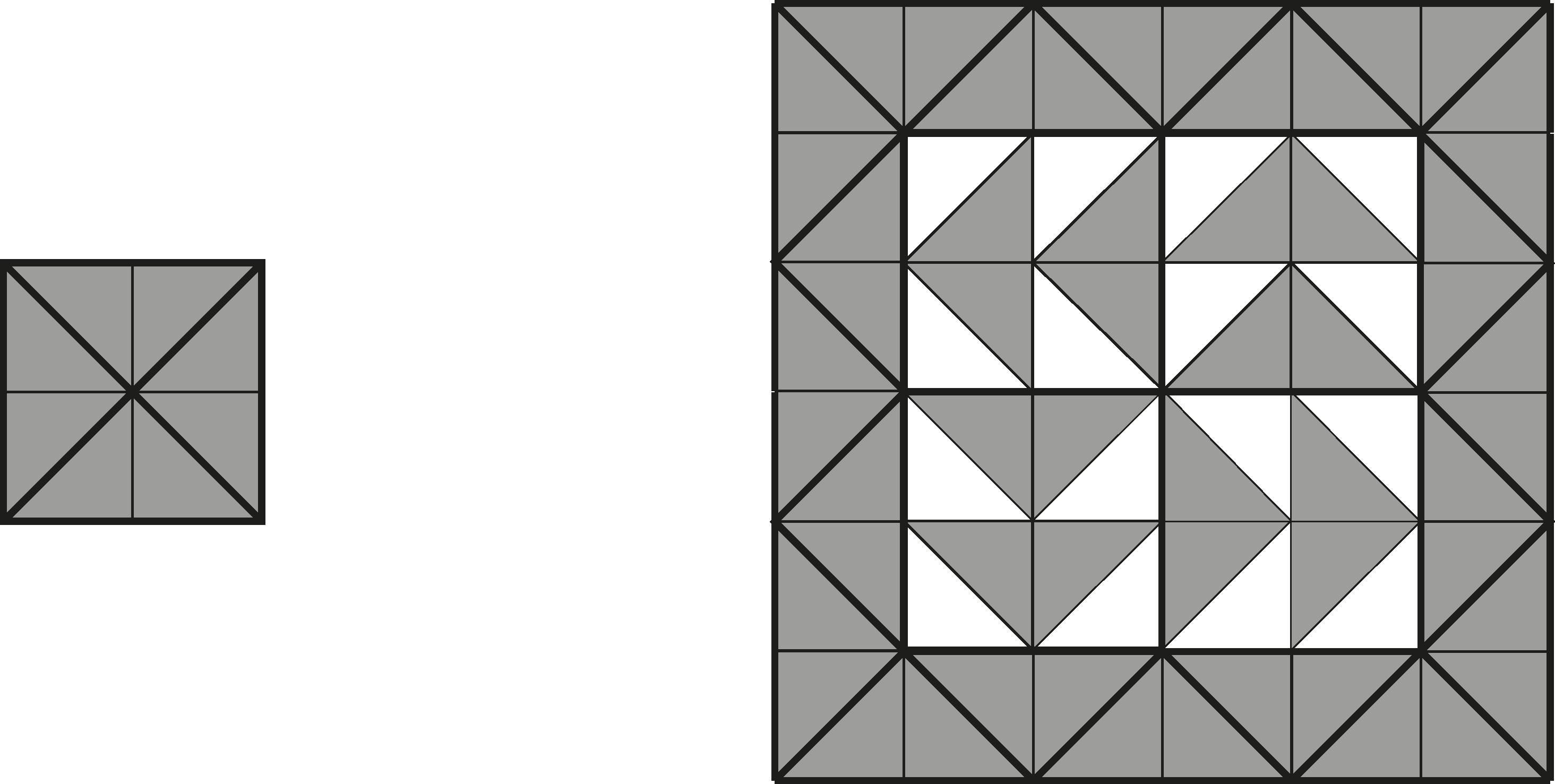
Štvorec \(2\times 2\) vydláždime priamočiaro a \(6\times 6\) dostaneme po chvíli hrania sa:
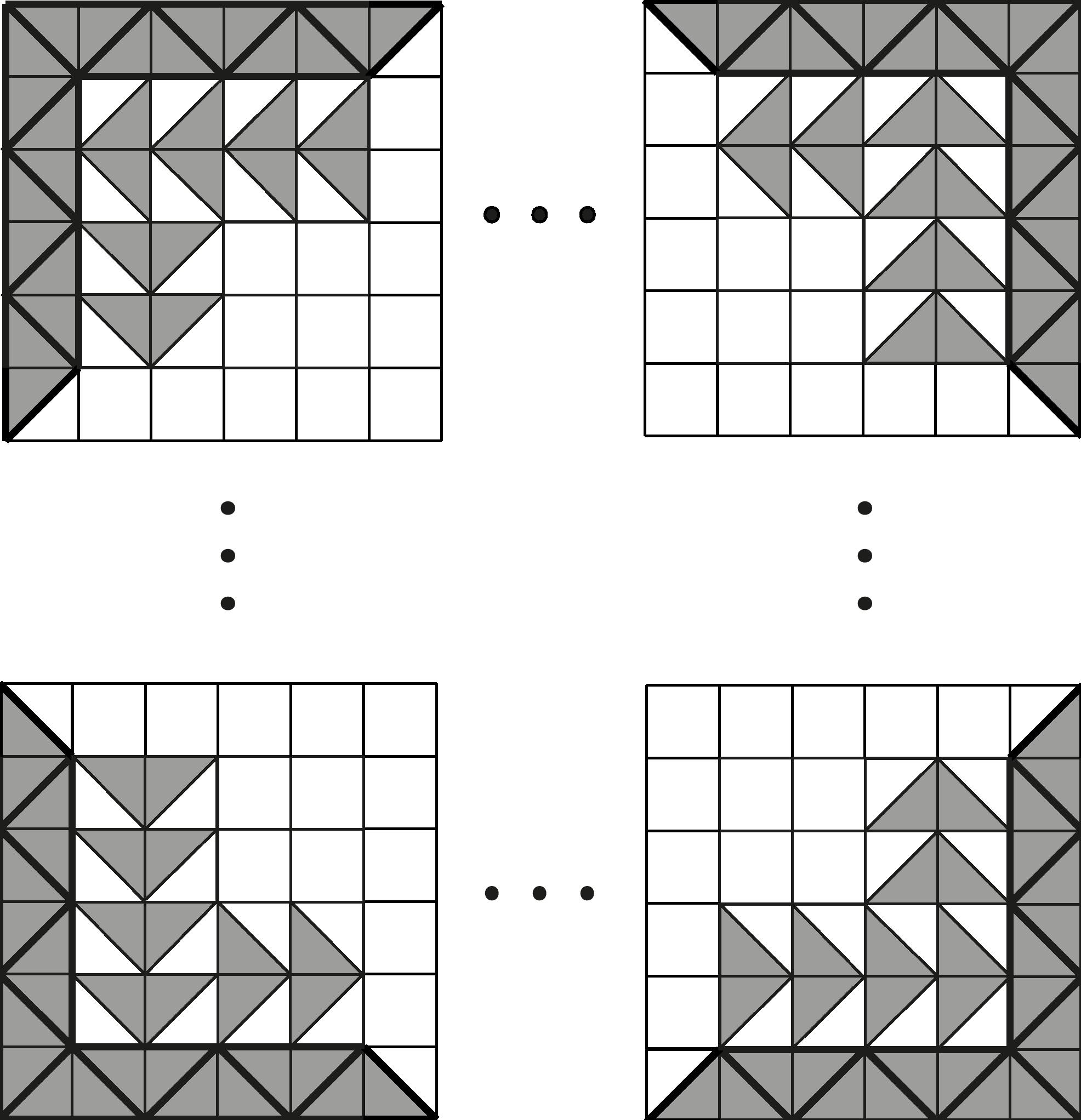
Takýmto obalovaním vieme zväčšiť rozmer vydláždeného štvorca o \(6\). Týmto sme dostali všeobecný postup, ako vydláždiť všetky štvorce pre \(n=6k\) a pre \(n=6k+2\), kde \(k\) je ľubovoľné .
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.