9. Kolinearita — Mirova Spokojnosť (vzorové riešenie) - Korešpondenčný matematický seminár

Zadanie

Mr. Miro je spokojný, keď je najedený. Okrem toho je spokojný aj vtedy, keď nájde tri body ležiace na jednej priamke.

Majme trojuholník $ABC$. Označme $A_1$, $B_1$, $C_1$ postupne body dotyku jeho vpísanej kružnice so stranami $BC$, $AC$, $AB$. Nech $O$ a $I$ sú postupne stredy kružnice opísanej a vpísanej trojuholníku $ABC$ a $H_1$ je ortocentrum trojuholníka $A_1B_1C_1$. Dokážte, že body $O$, $I$, $H_1$ ležia na jednej priamke.

Označme druhé priesečníky priamok $AI$, $BI$, $CI$ s kružnicou opísanou trojuholníku $ABC$ (nech je to kružnica $k$) postupne ako $K,\ L,\ M$. O týchto bodoch vieme, že sú to Švrčkove body k bodom $A,\ B,\ C$ v trojuholníku $ABC$.¹

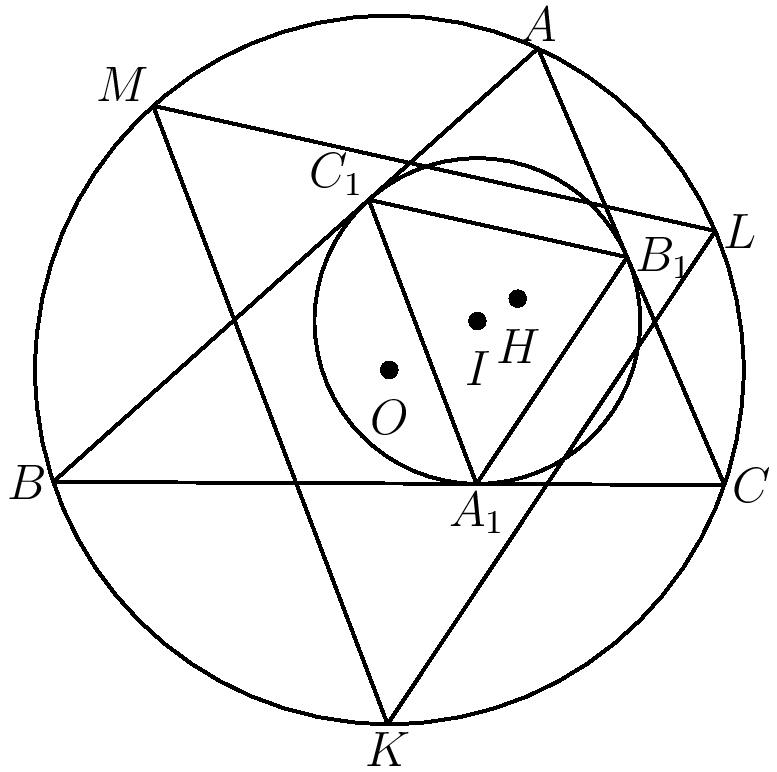
Ukážeme, že platí: $C_1B_1\parallel LM$. Zo známej vety o Švrčkových bodoch plynie, že vzdialenosť Švrčkovho bodu od „susediacich“ vrcholov je rovná jeho vzdialenosti od stredu vpísanej kružnice. Inak povedané pre našu úlohu platí $|LI|=|LA|$ a tiež $|MI|=|MA|$. To ale znamená, že štvoruholník $MILA$ je vlastne deltoid². Pre deltoid platí, že jeho uhlopriečky sú na seba kolmé. Teda $ML$ je kolmé na $IA$. Na $IA$ je však kolmá aj priamka $C_1B_1$, pretože štvoruholník $B_1IC_1A$ je tiež deltoid, dokonca s pravými uhlami. Preto evidentne $C_1B_1 \parallel LM$. Analogicky by sme sa vedeli dopracovať aj k rovnobežnostiam $KM\parallel A_1C_1$ a $KL\parallel A_1B_1$. Vidíme teda, že trojuholníky $A_1B_1C_1$ a $KLM$ sú nielen podobné, ale ich strany sú aj rovnako orientované.

Keďže sú rovnako orientované, tak existuje bod v rovine, ktorý je stredom rovnoľahlosti, ktorá zobrazuje trojuholník $A_1B_1C_1$ na trojuholník $KLM$. Toto je známy fakt, ale dalo by sa ho neformálne zdôvodniť tým, že v jednom zo stredov rovnoľahlostí kružníc $k$ a $l$ (kružnica opísaná trojuholníku $A_1B_1C_1$) sa tieto rovnobežné tetivy zobrazujú na seba. Označme si tento bod $S$.

Vieme, že aj významné body rovnoľahlých trojuholníkov sa na seba zobrazujú. Bod $I$ je zrejme stredom kružnice $l$, a preto sa v rovnoľahlosti so stredom $S$ zobrazí na bod $O$. Teda body $S,\ I,\ O$ ležia na jednej priamke. V trojuholníku $A_1B_1C_1$ je bod $H$ ortocentrom. Čo tak ukázať, že v trojuholníku $KLM$ je ortocentrom bod $I$?

To je ale ľahké, lebo z definície bodov $K,\ L,\ M$ platí, že trojice bodov $(K, I, A)$, $(L, I, B)$ a $(M, I, C)$ ležia na priamkach. O priamke $IA$ sme už ukázali, že je kolmá na $ML$ a pre zvyšné dve dvojice priamok je to analogické. Preto $I$ je skutočne ortocentrom trojuholníka $KLM$.

Teda bod $H$ sa v spomínanej rovnoľahlosti zobrazí do bodu $I$, a teda aj body $S,\ H,\ I$ ležia na priamke. To ale znamená, že aj body $H,\ I,\ O$ ležia na priamke, čo je presne to, čo sme chceli dokázať.

O Švrčkových bodoch si môžete prečítať v seriáli MKS Geometria trojuholníka od strany 29, ktorý nájdete na adrese http://mks.mff.cuni.cz/archive/36/serial.pdf ↩
Hoci všetci vieme, že je to kváder http://sedita.sk/vyrobky/oblatky/mila :)↩

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

9. Kolinearita — Mirova Spokojnosť vzorové riešenie

Zadanie

Diskusia