10. Kečupová Maľba Snov vzorové riešenie

Pri geometrií je užitočné si povedať, čo sa vlastne budeme snažiť dokázať. Celý obrázok pôsobí tak, že \(\triangle PKC\) a \(\triangle BAC\) by mohli byť rovnoľahlé podľa stredu \(C\). Ak by boli rovnoľahlé, tak aj pri bode \(K\) by bol pravý uhol a preto hľadaný \(\sphericalangle PKC\) by bol pravý.

Na riešenie tejto úlohy využijeme more podobných trojuholníkov a pomerov, ktoré platia medzi ich dĺžkami strán. Za inšpiráciu k tomuto riešeniu ďakujeme Majovi Poturnayovi. Odporúčaný spôsob čítania je zadívať sa na náčrt, postupne si overiť, že všetky uvedené vzťahy platia a nakoniec si užiť zlepenú skladačku.

V úlohe sú možné dve konfigurácie, prvá keď bod \(P\) leží na polpriamke \(BC\) (prípad, ktorý uvedieme) a druhá, keď bod \(P\) leží na polpriamke \(CB\). Druhú konfiguráciu je možné vyriešiť úpravou tohto postupu (iné trojuholníky budú podobné a iné uhly sa budú rovnať), ktorú odporúčame si rozmyslieť. Na obrázkoch uvádzame obe.

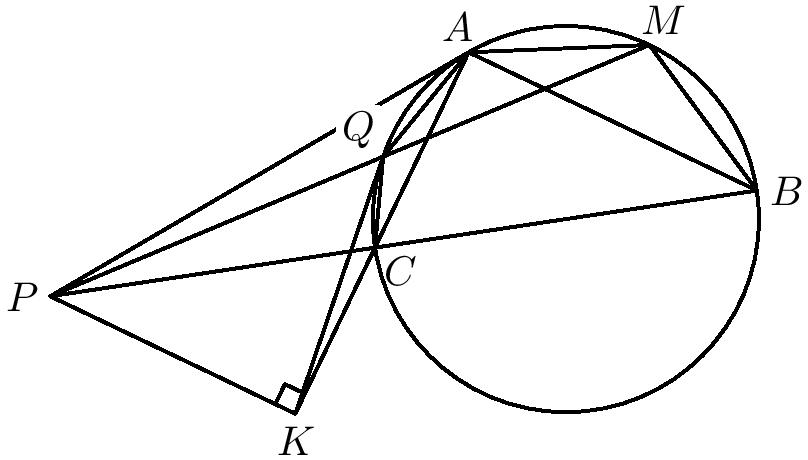
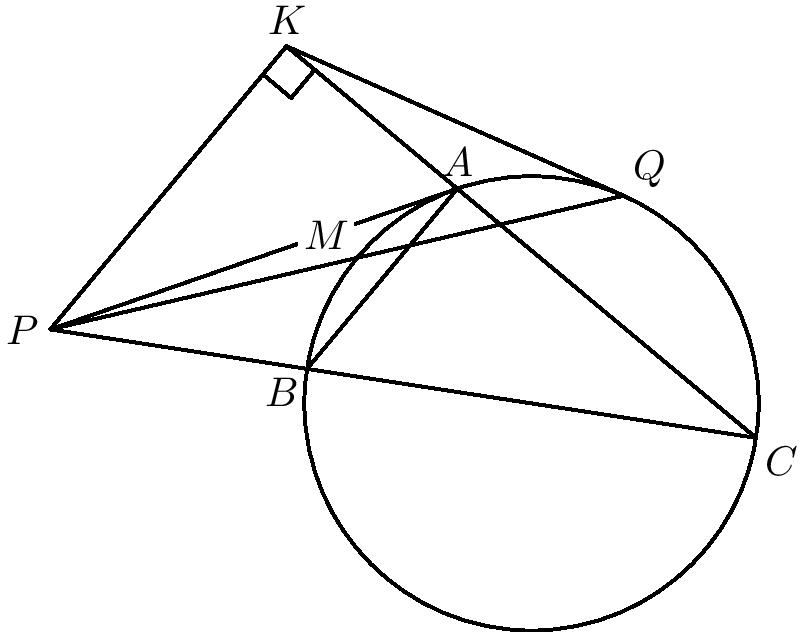
Všimnime si štvoricu bodov \(P\), \(C\), \(A\), \(B\). Tvorí typickú konfiguráciu pre použitie mocnosti. Môžeme si ale všimnúť aj úsekový uhol \(|\sphericalangle CBA|=|\sphericalangle PAC|\). Uhol pri vrchole \(P\) tvorí spolu s uvedeným úsekovým uhlom dva uhly, ktoré sú rovnaké v \(\triangle PCA,\, \triangle PAB\ (1)\). Tieto dva trojuholníky sú preto podobné. V rovnakej konfigurácii sú v úlohe aj dvojice: \(\triangle PQA,\, \triangle PAM\ (2)\) a \(\triangle KCQ, \triangle KQA\ (3)\). Pripravme si ešte poslednú dvojicu podobných trojuholníkov: \(\triangle PCQ, \triangle PMB\ (4)\). V tomto prípade \(|\sphericalangle PQC| = 180^\circ - |\sphericalangle CQM| = |\sphericalangle CBM|\) (posledná rovnosť vyplýva z toho, že \(CQMB\) je tetivový štvoruholník). Okrem toho oba trojuholníky majú spoločný uhol pri vrchole \(P\), čím je podobnosť dokázaná.

Aby boli \(\triangle PKC\) a \(\triangle BAC\) rovnoľahlé, musí platiť: \[\frac{|KC|}{|KA|}=\frac{|PC|}{|PB|}\] (Možno ste sa stretli s priamou definíciou rovnoľahlosti, kedy by sme tvrdili, že \(|KC|/|CA|=|PC|/|CB|\), nie je však ťažké si rozmyslieť, že uvedená rovnosť je s ňou ekvivalentná. Stačí si rozpísať dlhšie strany ako súčet menších častí a rovnicu upraviť.)

Upravujme postupne ľavú stranu. Vystupujú v nej body ako v \((3)\), odkiaľ vieme (dve rovnice následne vynásobíme): \[\frac{|KC|}{|KQ|}=\frac{|QC|}{|AQ|},\qquad \frac{|KQ|}{|KA|}=\frac{|QC|}{|AQ|} \quad \Rightarrow \quad \frac{|KC|}{|KA|} =\left(\frac{|QC|}{|AQ|}\right)^2\]

Postupne zo \((4)\) a \((2)\) vieme: \[\frac{|QC|}{|PQ|}=\frac{|MB|}{|PB|},\qquad \frac{|AQ|}{|PQ|} = \frac{|MA|}{|PA|} \quad \Rightarrow \quad \frac{|QC|}{|AQ|} = \frac{|MB|}{|MA|}\cdot\frac{|PA|}{|PB|}=\frac{|PA|}{|PB|}\] Dve rovnice sme vydelili a využili sme, že \(|MA|=|MB|\), lebo \(M\) je stred oblúka.

Použitím \((1)\), triviálne platného tvrdenia a ich vynásobením dostaneme: \[\frac{|PA|}{|PB|}=\frac{|PC|}{|PA|},\qquad \frac{|PA|}{|PB|} =\frac{|PA|}{|PB|} \quad \Rightarrow \quad \left(\frac{|PA|}{|PB|}\right)^2=\frac{|PC|}{|PB|}\]

Ostáva nám zložiť jednotlivé závery a tešiť sa: \[ \frac{|KC|}{|KA|}= \left(\frac{|QC|}{|AQ|}\right)^2= \left(\frac{|PA|}{|PB|}\right)^2= \frac{|PC|}{|PB|} \]