3. Kostra Mohutného Stanu (κ ≤ 3) vzorové riešenie

Pri takýchto úlohách je vždy dobrý začiatok skúsiť si do obrázka niečo dokresliť a potom skúmať, či tam niečo zaujímavé nevidíme. Spôsobov, ako do obrázka niečo dokresliť, je mnoho a niektoré dávajú väčší zmysel ako iné. V tomto konkrétnom prípade dávalo zmysel veľa rôznych dokreslení, my si ukážeme dve z nich.

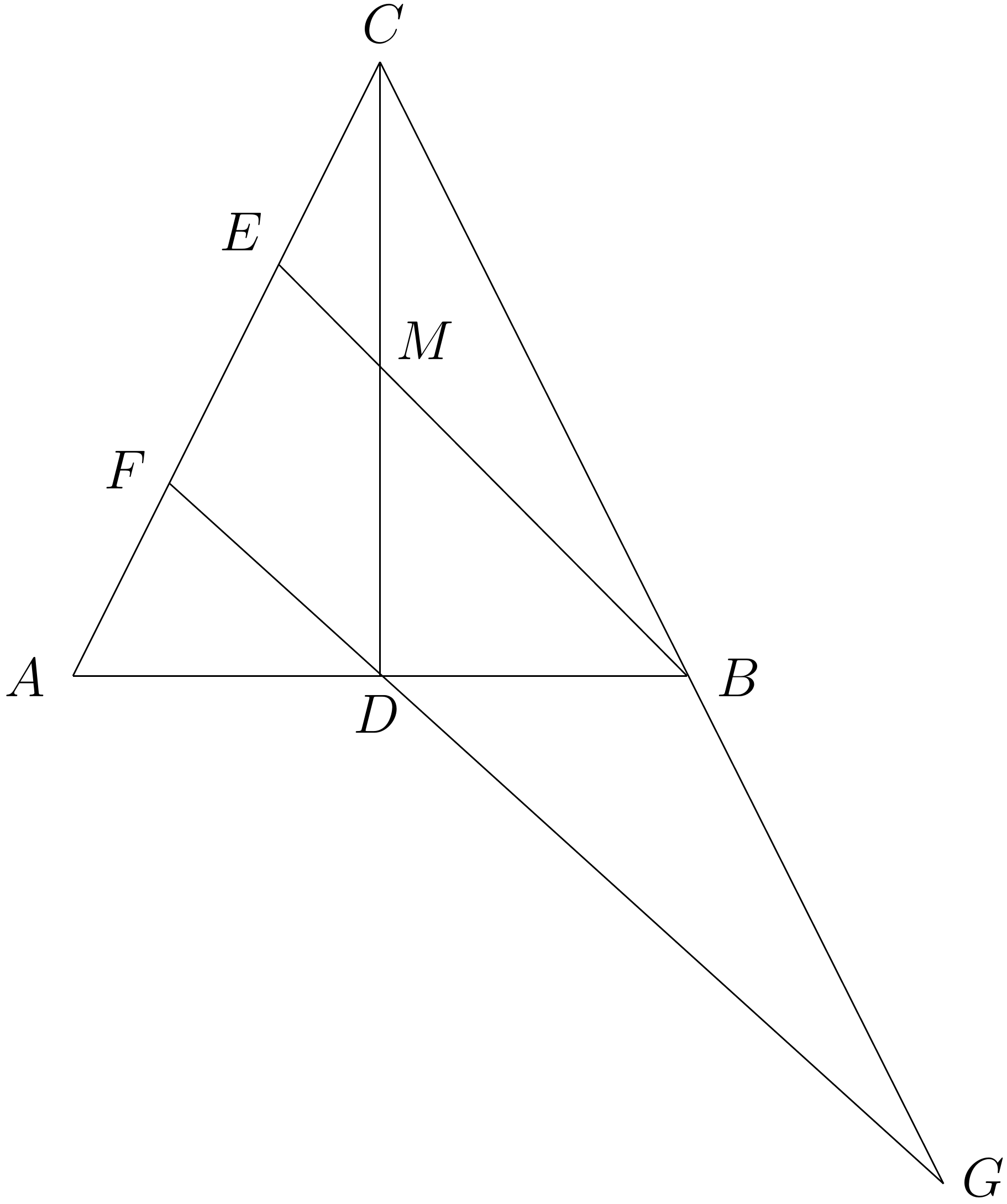
Najprv skúsime dokresliť priamku rovnobežnú s úsečkou \(EB\) prechádzajúcu bodom \(D\). Bod, v ktorom pretne stranu trojuholníka \(AC\), si nazveme \(F\) a bod, v ktorom pretne predĺženú stranu \(BC\), nazveme \(G\). Čo v takomto obrázku vidíme? Viacero trojuholníkov vyzerá podobne, napríklad taký \(\triangle MCE\) bude podobný s \(\triangle DCF\) podľa vety uu . Keďže úsečky \(DF\) a \(ME\) sú rovnobežné, veľkosti uhlov \(FDC\) a \(EMC\) sú rovnaké, a uhol \(FCD\) je spoločný. Vidíme, že trojuholník \(MCE\) je menší, no vieme ho natiahnúť tak, aby sa prekryl s (zobrazil sa na) trojuholníkom \(DCF\).

Zaujíma nás ako veľmi sa \(\triangle MCE\) pri tom zväčší, alebo inak povedané koľkokrát sú strany \(\triangle DCF\) dlhšie ako im prislúchajúce strany \(\triangle MCE\). Nie je to príliš náročné, keďže \(M\) leží v strede \(DC\), strana \(DC\) bude dvakrát dlhšia ako \(MC\). Pozrieme sa teda na stranu \(AC\) ktorá nás podľa zadania zaujíma, a s tým čo sme zistili vieme povedať, že strana \(FC\) je dvakrát dlhšia ako strana \(EC\) a teda platí, že \(EC\) a \(FE\) sú rovnako dlhé.

Fajn, toto však nie sú jediné podobné trojuholníky na obrázku, platí to aj pre \(\triangle ADF\) a \(\triangle ABE\), znova podľa uu (\(|\sphericalangle AFD| =|\sphericalangle AEB|\) a \(|\sphericalangle EAB|\) je spoločný). Znovu sa zamyslíme ako veľmi treba \(\triangle ADF\) natiahnúť aby bol rovnako veľký ako \(\triangle ABE\) – a vidíme že stačí potiahnúť bod \(D\) do bodu \(B\). Trojuholník \(ABC\) je rovnoramenný, bod \(D\) leží v strede strany \(AB\), a teda platí \(|AB|=2\cdot |AD|\). Pomer dĺžok prislúchajúcich strán \(\triangle ABE\) a \(\triangle ADF\) je teda znova \(2\), a znovu sa môžme pozrieť na stranu \(AC\). Platí \(|AE|=2\cdot |AF|\), takže \(|AF|=|EF|\).

A už máme všetko, čo potrebujeme, riešenie je zjavné. Platí \(|AF|=|EF|\) a \(|CE|=|EF|\), potom \(|AF|=|EF|=|CE|\). Čiže \(|AC|=3\cdot |CE|\) a \(|AE|=2\cdot |CE|\).

Iné riešenie

Ako sme spomínali, ukážeme si dve riešenia, tu je druhé. Teraz využijeme symetriu rovnoramenného trojuholníka a dokreslíme si okolo neho obdĺžnik \(ABXY\) tak, že bod \(C\) leží v strede strany \(XY\). Bod \(M\) nám tak nejako intuitívne pripadá byť stredom nášho obdĺžnika, a bez väčšej námahy to aj vieme ukázať (nech sa páči). Úsečka \(BM\) začína vo vrchole obdĺžnika a pokračuje do jeho stredu, ak ju teda predĺžime bude z nej uhlopriečka a narazí na bod \(Y\). Rovnako zakreslíme aj druhú uhlopriečku \(AX\).

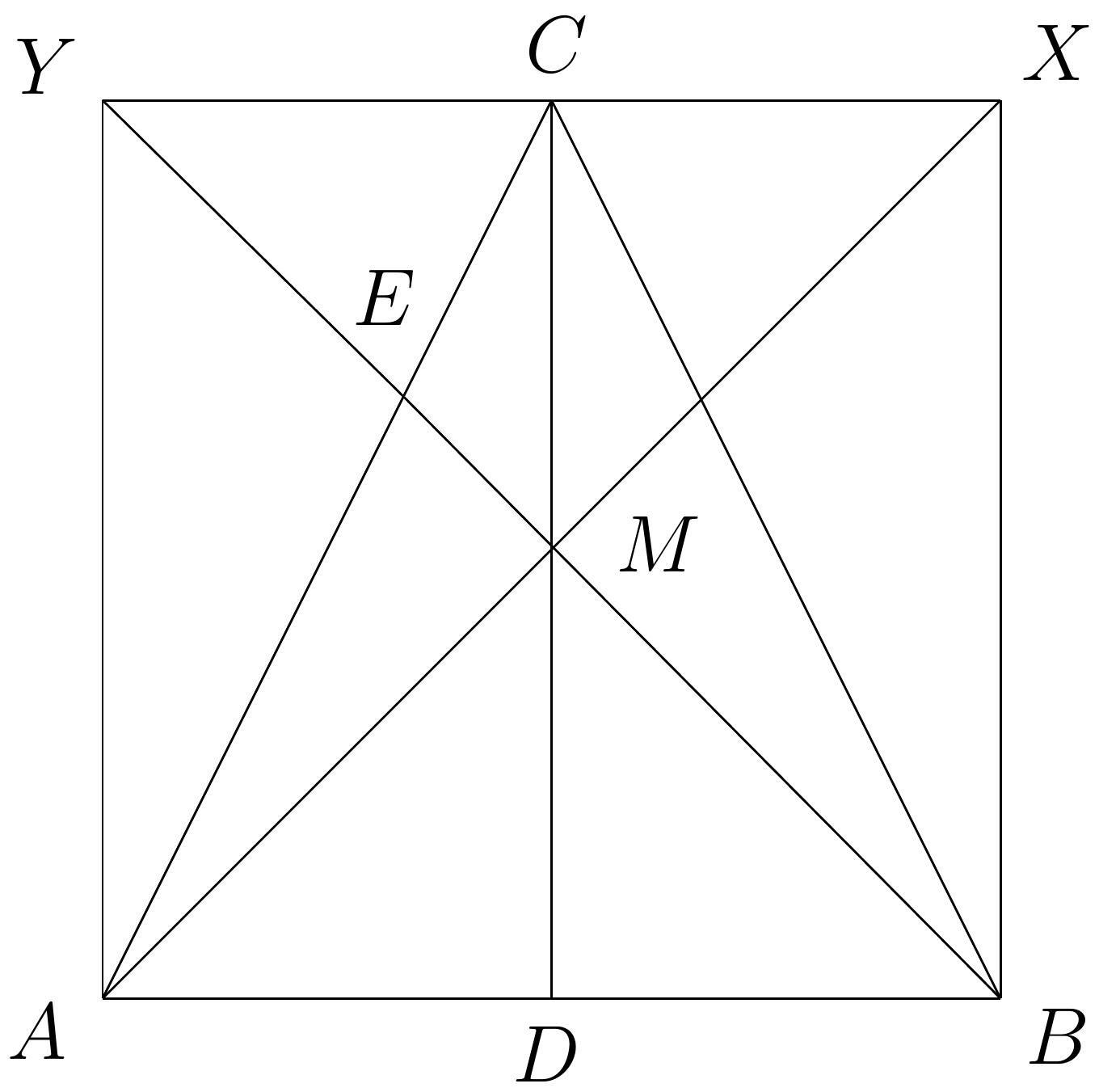
Teraz sa zamerajme na trojuholník \(AXY\). Strana \(AC\), ktorá nás podľa zadania zaujíma, spája jeho vrchol so stredom protiľahlej strany, bude teda ťažnicou. Bod \(M\) delí uhlopriečky na polovice a teda leží v strede \(AX\). Z toho ale vyplýva že aj \(YM\) je ťažnica trojuholníka \(AXY\). Bod, v ktorom sa pretínajú ťažnice, nazývame ťažiskom a v tomto prípade je to bod \(E\). Vieme že ťažisko leží v dvoch tretinách ťažnice, čo je dosť príhodné lebo to priamo dokazuje že \(|AE|=2\cdot |CE|\). A voilà, máme hotovo!