5. Koľko Miesta Separuješ? (κ ≤ 7) vzorové riešenie

Máme \(n\) trojuholníkov na papieri. Čo nás zaujíma je, že koľko oblastí je týmito trojuholníkmi (ich obvodmi) ohraničených. Najskôr sa pozrime na to, aká môže byť vzájomná poloha týchto trojuholníkov. Najjednoduchšie, čo sa môže stať je, že sa vôbec neprekrývajú a teda pre \(n\) trojuholníkov dostávame za každý trojuholník jeden kus papiera, teda \(n+1\) kusov papiera (plus zvyšok). Ďalšia jednoduchá možnosť nastáva, ak sú všetky trojuholníky zhodné a položené na sebe. Vtedy dostaneme len \(2\) oblasti, ale keďže nás zaujíma, koľko najviac častí môžno získať, tak túto možnosť môžeme ignorovať.

Získali sme nejaký spodný odhad na počet oblastí. To je na začiatok fajn, ale zrejme to nie je najlepšie umiestnenie. Je teda úplne na mieste položiť si otázku, čo by sa muselo stať, aby sme získali viac oblastí. Veľa možností, čo robiť, nemáme, skúsme umiestniť trojuholníky tak, aby sa pretínali. To nám pridá pár ďalších oblastí. Pozrime sa najprv na malé prípady, čo sa udeje, keď budu trojuholníky len dva. Po chvíľke skúšania dôjdeme k tomu, že vieme dostať najviac \(8\) oblastí. Napríklad takto:

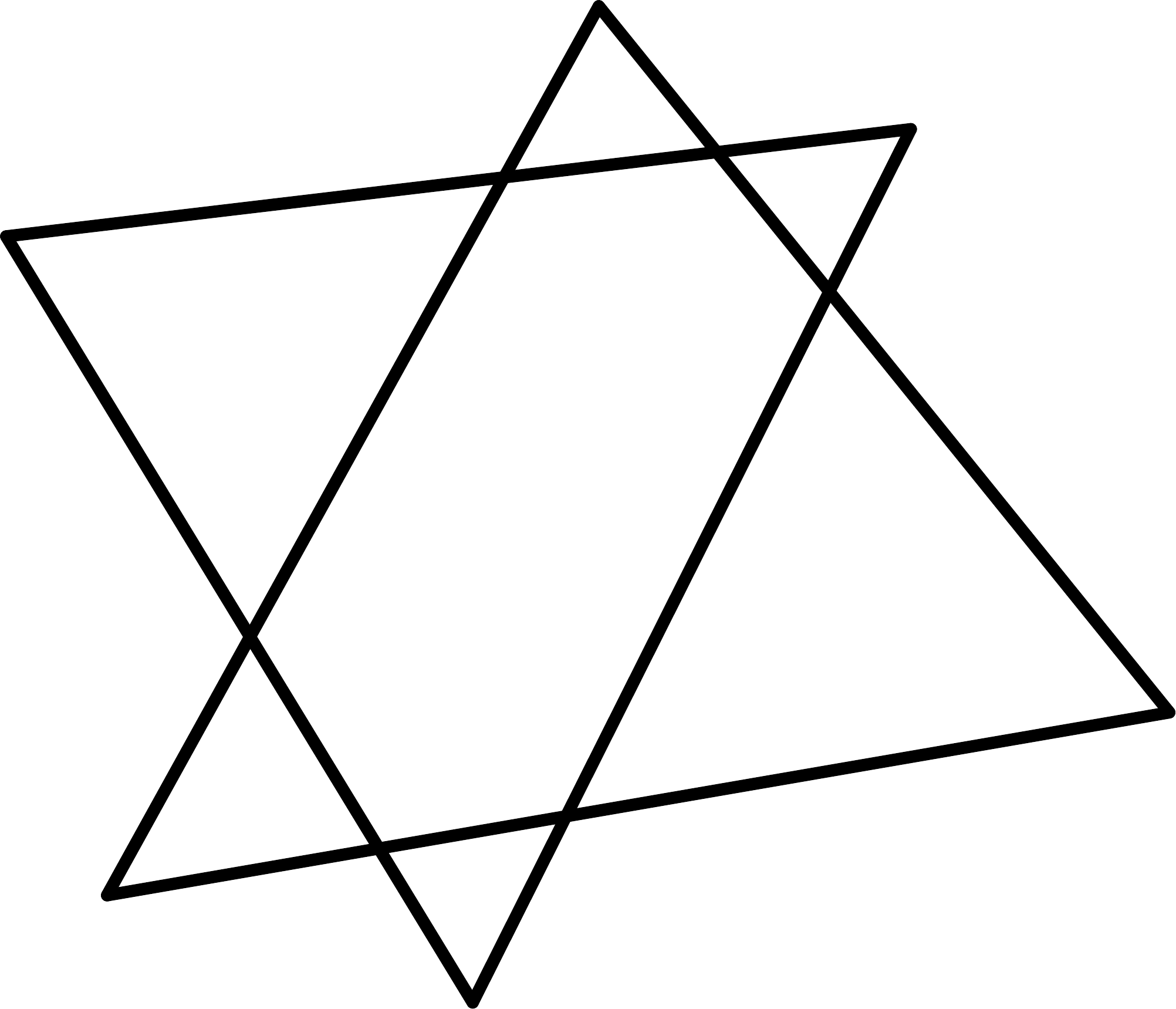
Pozrime sa lepšie na to ako môže vzniknúť nová oblasť. Nová oblasť nám vznikne vtedy, keď niektorá zo strán trojuholníka pretne dvakrát iný trojuholník, lebo ho tým rozdelí na dve časti, alebo ak nejaký nejaký vrchol leží na strane iného trojuholníka. Rozmyslime si, že v takom prípade by sme mohli trojuholníky preusporiadať tak, aby sa na vzájomnej polohe všetkých iných trojuholníkov nič nezmenilo a počet oblastí by bol väčší (tento nový vrchol by sme posunuli tak, aby sa tieto trojuholníky preťali). Preto ďalej uvažujme len možnosť kedy žiadny vrchol neleží na strane iného trojuholníka. Jedna úsečka teda vie pretnúť trojuholník najviac dvakrát. Pozrime sa, čo sa môže stať, keď máme ľubovoľne položených \(n\) trojuholníkov a chceli by sme pridať \((n+1)\)-vý .

Najviac oblastí dostaneme práve vtedy, ak každá strana novo pridaného trojuholníka pretne každý iný trojuholník práve dva krát, čo tak isto znamená, že každá zo strán pôvodných trojuholníkov dvakrát pretne náš novo pridaný trojuholník. Pôvodných strán máme \(3n\), teda náš nový trojuholník vie delením pôvodných trojuholníkov pridať najviac \(3n\) oblastí. Tak isto ale strany pôvodných trojuholníkov vedia pretnúť novo pridaný najviac dvakrát, teda dokopy to je \(6n\). Oblasť ohraničenú novo pridaným trojuholníkom rátať nemusíme, lebo je už započítaná v spoločnom prieniku všetkých trojuholníkov. (Ak sa nám podarí trojuholník umiestniť tak, aby každá strana bola dvakrát pretnutá.)

Keďže pri jednom trojuholníku sú \(2\) oblasti, tak takýmto pridávaním trojuholníkov ich nebude viac ako \(2+6+12+\dots +(6n-6) = 2+6(1+2+\dots+(n-1)) = 2+ 3n(n-1).\) Ešte potrebujeme ukázať, že existuje rozloženie trojuholníkov, pre ktoré je možné daný počet oblastí dosiahnuť. Na to také rozloženie zostrojíme.

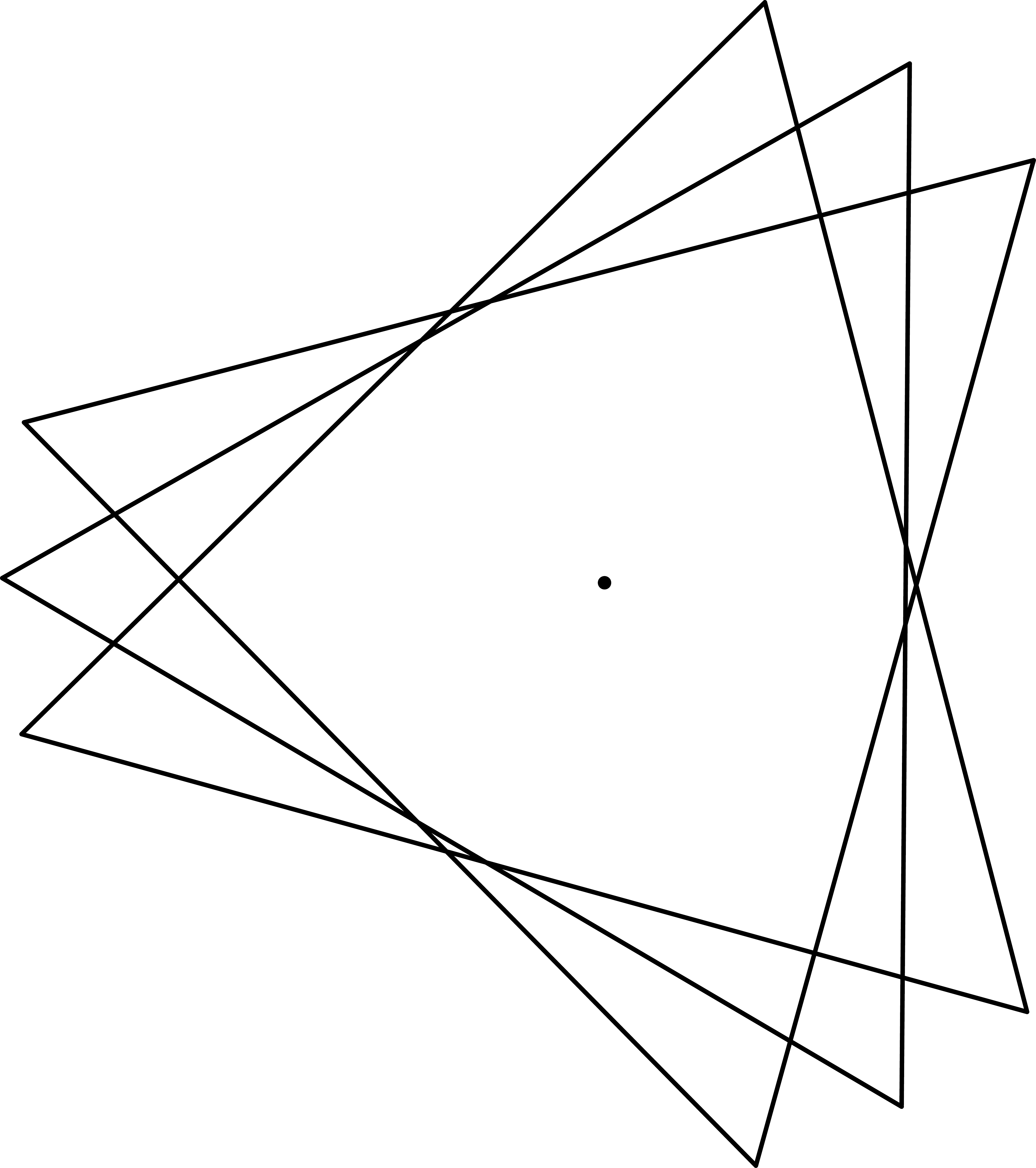
Vezmeme si rovnostranný trojuholník a ten \(n\)-krát otočíme okolo svojho ťažiska tak, aby trojuholníky spolu nesplynuli.

Iné riešenie

Pri skúšaní, ako dostať čo najviac oblastí, si môžeme všimnúť, že čím viac sa nám trojuholníky pretnú, tým viac oblastí dostaneme. Na to, aby sme mohli niečo také dokázať, by sa nám zišlo najprv poriadne uchopiť „pretnutie trojuholníkov“. Čo nám určí, ako veľa sa trojuholníky pretínajú? Napríklad priesečníky. Prečo by mal počet priesečníkov nejako súvisieť s počtom oblastí, ktoré dostaneme? Lebo vždy, keď sa nám niektoré dva trojuholníky pretnú, tak vznikne aj nová oblasť aj nové priesečníky.

Poďme skúsiť dokázať, že čím viac je priesečníkov, tým viac je oblastí. Táto úloha nám môže znieť povedome. Vzťah medzi počtom oblastí a počtom priesečníkov je zachytený Eulerovým vzorcom. Ten hovorí, že \[\text{počet hrán (úsečiek medzi vrcholmi a priesečníkmi)} - \text{počet vrcholov (priesečníkov)} = \text{počet oblastí} - 2.\] (Ak ste o ňom nepočuli, pozrite si to tu https://sk.wikipedia.org/wiki/Rovinn%C3%BD_graf). No a teda prečo by sme mali chcieť, aby sme mali čo najviac priesečníkov? Pretože ak sa nejaké dve strany trojuholníka pretnú, tak za každú dvojicu pretnutých strán dostaneme síce jeden nový priesečník, ale zároveň dve nové hrany (úsečky). Teda za jeden nový priesečník dostávame navyše jednu oblasť.

Keďže každý priesečník pridáva \(2\) hrany, počet hrán sa dá vyjadriť ako \(3n + 2\) (počet priesečníkov). Po dosadení do Euklidovho vzorca dostávame, že: (\(3n + 2\) (počet priesečníkov)) \(-\) (počet priesečníkov \(+\) počet vrcholov) \(=\) (počet oblastí) \(- 2\), teda počet oblastí \(= 3n + 2 +\) (počet priesečníkov) \(-\) (počet vrcholov). Keďže vrcholov je \(3n\), dostávame, že počet oblastí \(= 2 +\) počet priesečníkov. Stačí nám teda docieliť maximálny počet priesečníkov.

Dva trojuholníky sa môžu pretnúť najviac \(6\)-krát (rozmyslite si). Ak by sa nám podarilo vymyslieť takú konštrukciu, že každá dvojica trojuholníkov sa pretína práve \(6\times\) a žiadne tri trojuholníky sa nepretínajú v jednom bode, dostaneme najväčší možný počet priesečníkov a teda aj oblastí. To, že to je naozaj možné vyplýva z konštrukcie, ktorá je rovnaká ako v predchádzajúcom riešení.

Vezmeme si rovnostranný trojuholník a ten \(n\)-krát otočíme okolo svojho ťažiska tak, aby trojuholníky spolu nesplynuli. (Rozmyslite si, že priesečníky dvoch rôznych dvojíc trojuholníkov nemôžu splynúť.) Ľahko overíme, že pre \(n\) vieme dostať najviac \(n(n-1)3 +2\) oblastí.