10. Kynoženie Mestských Snejkov vzorové riešenie

Zadnie. V hlavnom meste kolónie dokončujú námestie. Plochu \((2^{n} + 1)\times(2^{n}+1)\) chcú vydláždiť bielymi a čiernymi dlaždicami rozmeru \(1 \times 1\). Dláždiť musia tak, aby z čiernych dlaždíc nevznikol uzavretý hadík. V závislosti od kladného celého čísla \(n\) určte, koľko najviac čiernych dlaždíc môžu použiť?

Poznámka. Uzavretý hadík je postupnosť \(k \ge 4\) rôznych čiernych dlaždíc \(a_1,\, a_2,\, \dots,\, a_k\) takých, že dlaždice \(a_{i}\) a \(a_{i+1}\) pre \(i \in \{1,2,\dots,k-1\}\) a taktiež dlaždice \(a_k\) a \(a_1\) majú spoločnú hranu.*

Prvotné úvahy

Na začiatok si môžeme vyriešiť úlohu pre prípad \(n = 1\), teda pre námestie rozmerov \(3 \times 3\). Ľahko prídeme na to, že najviac možno použiť \(7\) čiernych dlaždíc, napríklad nasledovnými spôsobmi:

Môžeme pristúpiť k vyšším rozmerom. Jeden spôsob, ktorý môžeme odpozorovať s prvých dvoch dláždení námestia \(3 \times 3\), je skúsiť vytvoriť z čiernych dlaždíc jedného dlhého zamotaného hadíka. Pri námestí \(5 \times 5\) tak použijeme \(17\) čiernych dlaždíc.

Ak sa trochu viac pohráme a skúsime sa inšpirovať tretím spôsobom, kde sa čierne dlaždice akoby „rozvetvujú“, môžeme objaviť vydláždenie využívajúce \(19\) čiernych dlaždíc.

Môžeme skúšať vydláždiť námestie \(9 \times 9\), ale zatiaľ sa nám tu nerysuje žiaden očividný systém, ako najlepšie dláždiť. Môžeme sa skúšať hrať a nachádzať čo najlepšie spôsoby dláždenia. Ale pokiaľ chceme úlohu vyriešiť, tak raz budeme musieť ukázať, prečo nemôže byť čiernych dlaždíc viac. Preto sa pokúsime najskôr získať nejaký horný odhad, aby sme vytušili, kedy s našimi hrátkami skončiť.

Horný odhad

Ako môžeme získať nejaký horný odhad? Čo za vec sú uzavreté hadíky? Nepripomínajú nám nejaký známy matematický pojem? Podobné veci možno nájsť v teórii grafov. Graf sa skladá z vrcholov a hrán, kde niektoré dvojice vrcholov sú spojené hranou. V teórie grafov máme pojem cyklus, ktorý celkom dobre odpovedá uzavretému hadíkovi. O cykloch v grafe vieme povedať, že graf neobsahujúci cyklus má menej vrcholov ako hrán. Skúste si to dokázať.¹

Takže nejaký odhad by sme vedeli získať porovnaním počtu vrcholov a hrán. Najprv však musíme prerobiť naše námestie na graf, ktorý si pomenujeme \(G\). Zvolíme pri tom celkom priamočiary postup. Čierne dlaždice budú zodpovedať vrcholom grafu \(G\) a dva vrcholy spojíme hranou, ak im odpovedajúce čierne dlaždice majú spoločnú stranu. Ak označíme \(c\) počet čiernych dlaždíc, tak náš graf má \(c\) vrcholov. Teraz odhadneme zhora počet jeho hrán.

Označme si \(m = 2^n + 1\). Zoberme si graf \(H\), ktorý zodpovedá námestiu rozmerov \(m \times m\), ktoré je celé vydláždené načierno. Graf \(H\) má \(m\) vrcholov a \(2m(m-1)\) hrán. Graf \(G\) z neho dostaneme tak, že odstránime \(b = m^2 - c\) bielych políčok. Každé biele políčko odstráni najviac \(4\) hrany. Preto počet hrán grafu \(G\) bude aspoň \(2m(m-1) - 4b = 2m(m-1) - 4m^2 + 4c = 4c - 2m^2 - 2m\). Keďže graf \(G\) je bez cyklu, tak musí obsahovať menej hrán ako vrcholov, teda \[ \begin{aligned} 4c - 2m^2 - 2m &< c,\\ c &< \frac{2m(m + 1)}{3}. \end{aligned} \] Dostávame tak, že počet použitých čiernych dlaždíc pri dláždení námestia \(m \times m\) môže byť najviac \[\frac{2m(m+1)}{3} - 1 = \frac{2(2^n + 1)(2^n + 2)}{3} - 1 = \frac{2\cdot 4^n + 6\cdot 2^n + 4 - 3}{3} = \frac{2 \cdot 4^n + 1}{3} + 2^{n+1}.\]

Myšlienka konštrukcie

Odhad, ktorý sme získali, je super, lebo pre \(n = 2\) (námestie \(5 \times 5\)) dostávame, že \(19\) je naozaj najväčší možný počet čiernych dlaždíc. Skúsme teda nájsť nejaký postup, ako vydláždime námestia všetkých možných rozmerov. Náš odhad nám aj môže pomôcť pri hľadaní riešenia. Aby sme ho dosiahli, musia takmer všetky biele dlaždice susediť so štyrmi čiernymi.

Môžeme si všimnúť, že dláždenie námestia \(5 \times 5\) sa dá poskladať zo štyroch dláždení námestí \(3 \times 3\) s tým, že ešte jednu dlaždicu prefarbíme nabielo.

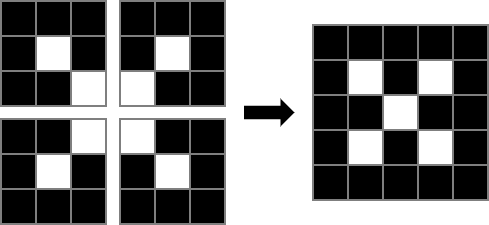
Ak tento postup zopakujeme, vieme dostať námestie rozmerov \(9 \times 9\) vydláždené \(59\) čiernymi dlaždicami, čo je z nášho odhadu najväčší možný počet. Vyzerá to teda sľubne, tak skúsme tento postup všeobecne opísať.

Konštrukciu pôjdeme teda popisovať induktívne, tzn. pomocou dláždenia menších námestí vydláždime väčšie námestie.

Konštrukcia

Námestie rozmerov \(3 \times 3\) vydláždime ako na prvom obrázku. Námestie rozmerov \((2^n + 1) \times (2^n + 1)\) vydláždime nasledovne: Prostredný riadok a prostredný stĺpec vydláždime načierno okrem ich spoločného políčka, kam dáme bielu dlaždicu. Takto sa nám námestie rozdelí na štyri oblasti rozmerov \((2^n + 1) \times (2^n + 1)\) vychádzajúce z jeho rohov. Každú oblasť vydláždime ako vhodne otočené námestie rozmerov \((2^n + 1) \times (2^n + 1)\). Nakoniec čiernu dlaždicu v pravom dolnom rohu vymeníme za bielu.

Všimnime si, že každé takto vydláždené námestie má na obvode len čierne dlaždice okrem jednej rohovej dlaždice, ktoré je biela.

Ak počet bielych dlaždíc vo vydláždení námestia \((2^n + 1) \times (2^n + 1)\) označíme \(p_n\), platí \(p_{n+1} = 4p_n - 3\) pre každé celé \(n \ge 1\) a \(p_1 = 2\). Tento počet vieme vyjadriť aj ako \(p_n = (4^n + 2)/3\), čo vieme ľahko ukázať matematikcou indukciou. Počet čiernych dlaždíc je teda \[ (2^n + 1)^2 - \frac{4^n + 2}{3} = 4^n + 2\cdot 2^n + 1 - \frac{4^n + 2}{3} = \frac{2\cdot 4^n + 1}{3} + 2 \cdot 2^n,\] čo presne zodpovedá nášmu hornému odhadu.

Ostáva nám teda len ukázať, že v takomto vydláždení nie je uzavretý hadík z čiernych dlaždíc. Pre spor predpokladajme, že ho tam máme a že bez ujmy na všeobecnosti prechádza ľavou hornou oblasťou. Z indukčného predpokladu vieme, že iba v jednej oblasti hadík nemôže byť. Musí teda vychádzať z ľavej hornej oblasti a vchádzať do nej. Ak by vychádzal aj vchádzal na tej istej strane, dostaneme hadíka v prvej oblasti. Preto hadík z ľavej hornej oblasti musí prechádzať aj pravou hornou, aj ľavou dolnou oblasťou. Aby sa uzavrel, musí prechádzať aj pravou dolnou oblasťou, teda všetkými oblasťami.

Každý hadík musí prechádzať všetkými štyrmi oblasťami. Pritom do každej oblasti vchádza a vychádza na iných stranách. Zoberme si pravú dolnú oblasť \(O\), do ktorej vchádza hadík na kachličke \(X\) a vychádza na kachličke \(Y\). Hadík neprechádza pravým dolným rohom, keďže sa tam nachádza biela kachlička. Keď ju však vymeníme za čiernu, dostaneme vyhovujúce dláždenie oblasti \(O\). Avšak teraz sa možno z kachličky \(X\) dostať do kachličky \(Y\) aj po obvode oblasti \(O\) cez pravý dolný roh. Spojením týchto dvoch ciest vieme nájsť v oblasti \(O\) uzavretého hadíka (skúste si riadne dokázať, že taký existuje). To je však spor, lebo z indukčného predpokladu dláždenie tejto oblasti žiadneho neobsahovalo.

Ukázali sme teda, že naše dláždenie námestia \((2^{n + 1} + 1) \times (2^{n + 1} + 1)\) neobsahuje žiadnych hadíkov a taktiež, že používa najväčší možný počet čiernych dlaždíc.

Iná konštrukcia

Ilustrujeme ešte jeden spôsob, ako vydláždiť námestie \((2^n + 1) \times (2^n + 1)\) s najväčším možným počtom dlaždíc. Začne tým, že čierne dlaždice poukladáme šachovnicovo tak, že rohy nám ostanú voľné. Pozrime sa políčka v nepárnom riadku a zároveň v nepárnom stĺpci (ak máme riadky aj stĺpce očíslované od \(1\) po \(2^n + 1\)), ktoré si vyfarbíme načerveno.

Z červených políčok si vieme vytvoriť červené námestie rozmerov \((2^{n - 1} + 1) \times (2^{n-1} + 1)\). Ak na červené políčka uložíme biele a čierne dlaždice, tak uzavretý čierny hadík v námestí \((2^n + 1) \times (2^n + 1)\) zodpovedá uzavretému čiernemu hadíkovi v červenom námestí. Preto ak červené políčka vydláždime najlepším dláždením námestia \((2^{n - 1} + 1) \times (2^{n-1} + 1)\), v dláždení námestia \((2^n + 1) \times (2^n + 1)\) nám nevznikne žiaden uzavretý hadík. To, že takéto dláždenie obsahuje \((2\cdot 4^n + 1)/3 + 2\cdot 2^n\) čiernych dlaždíc ponechávame na čitateľa.

Komentár

Vo väčšine úloh, kde hľadáme najväčší (príp. najmenší) počet niečoho, v kategórii BETA je jednoduchšia časť nájsť riešenie a spôsob, ako ho dosiahnuť. V tejto úlohe boli pomerne obtiažne obe časti. Preto hoci pre mnohých z vás je zdôvodňovanie, že viac dlaždíc nemožno použiť, tá menej obľúbená časť, bol tu priestor na hľadanie najlepšieho spôsobu dláždenia. Za nájdenie najväčšieho možného počtu čiernych dlaždíc a ukázanie spôsobu dláždenia, ako ho dosiahnuť vrátane dôkazu, že vyhovuje zadaniu, bolo možné získať až 5 bodov.