2. Krásny Medzinárodný Symbol (κ ≤ 2) vzorové riešenie

Zadanie

Jožo na letisku narazil na zaujímavý amulet ako na obrázku. Pozostával z dvoch rovnostranných trojuholníkov. Predavačka mu prezradila, že vzdialenosť každého bodu obvodu malého trojuholníčka k najbližšiemu bodu obvodu veľkého trojuholníka je \(\sqrt{3}\). Určte rozdiel medzi dĺžkami strán malého a veľkého trojuholníka.

Pri riešení geometrických úloh je dobré nakresliť si obrázok a uvedomiť si všetky informácie, ktoré máme k dispozícii. Zo zadania vieme, že vzdialenosť každého bodu obvodu malého trojuholníka je vzdialená od veľkého trojuholníka \(\sqrt{3}\). V praxi to znamená, že ak spravíme kolmicu, z ktoréhokoľvek bodu malého trojuholníka na najbližšiu stratnu veľkého trojuholníka, tak jej dĺžka bude \(\sqrt{3}\). Ďalšia dôležitá vec, ktorú vieme zo zadania, je, že oba trojuholníky sú rovnostranné. Takže ich vnútorné uhly majú veľkosti \(60^\circ\), a teda tieto dva trojuholníky sú podobné podľa vety \(uuu\). Keďže, vzdialenosť malého trojuholníka od veľkého je na všetky smery rovnaká, nachádza sa presne uprostred veľkého trojuholníka, a teda majú tieto trojuholníky aj spoločné ťažisko (bod, v ktorom sa pretínajú ťažnice, pri rovnostrannom trojuholníku aj výšky). Označme si veľký trojuholník písmenami \(ABC\) a malý \(DEF\). Dĺžku strany malého trojuholníka označíme písmenom \(a\). Urobíme kolmý priemet strany \(EF\) malého trojuholníka na stranu \(BC\) veľkého trojuholníka, túto úsečku si označíme písmenami \(M\) a \(N\) a jej dĺžka je rovná \(a\). Zvyšné dve časti strany \(BC\) veľkého trojuholníka, ktoré nám vznikli, teda úsečky \(CM\) a \(NB\), majú rovnakú veľkosť, ktorú si označíme \(x\).

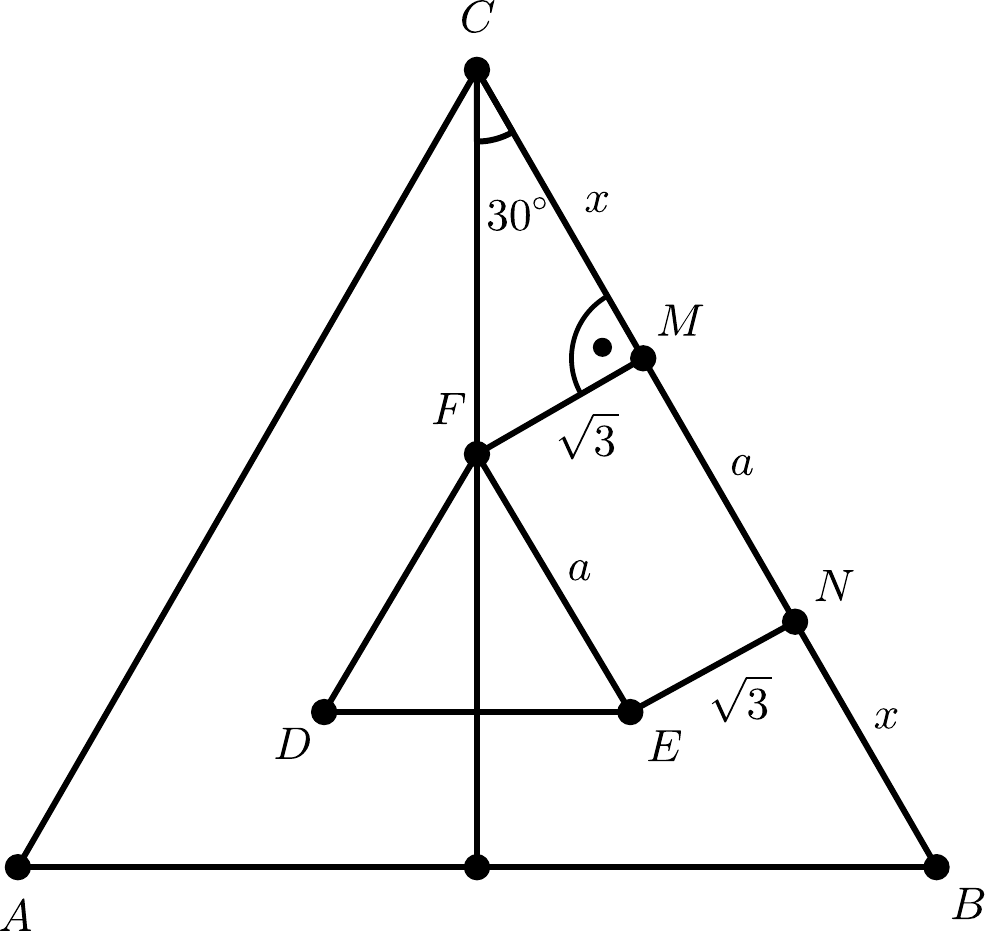
Teraz si treba uvedomiť, čo chceme vypočítať. Chceme rozdiel dĺžky strany veľkého trojuholníka od dĺžky strany malého trojuholníka. Vidíme, že obe strany obsahujú dĺžku strany \(a\), takže po odčítaní sa tieto dĺžky vyrušia a ostane nám len dvakrát dĺžka \(x\). A to teraz potrebujeme vypočítať. Ak spravíme výšku na stranu \(AB\) z bodu \(C\) nášho veľkého trojuholníka, rozdelí sa nám uhol pri vrchole \(C\) na polovicu, a teda na dva \(30^\circ\) uhly. Platí to vďaka tomu, že trojuholník je rovnostranný. Táto výška prechádza rovnako aj cez vrchol \(F\) (vďaka spoločnému ťažisku trojuholníkov). Vznikol nám pravouhlý trojuholník \(FMC\), s pravým uhlom pri vrchole \(M\) (keďže z vrcholu \(F\) sme viedli kolmicu) a s \(30^\circ\) uhlom pri vrchole \(C\). Rovnako tento postup vieme aplikovať aj na ostatné vrcholy trojuholníka vďaka symetrii. Ukážeme si teraz dva možné postupy výpočtu, prvý čo využíva goniometrické funkcie a druhý s použitím Pytagorovej vety.

Riešenie cez goniometrické funkcie

Keďže máme pravouhlý trojuholník, vieme použiť goniometrické funkcie na výpočet dĺžky \(x\). Máme zadanú dĺžku jednej odvesny trojuholníka \(FMC\) a potrebujeme zistiť dĺžku druhej odvesny. Takže môžeme využiť goniometrickú funkciu tangens alebo kotangens. Tangens uhla je definovaný ako pomer protiľahlej a priľahlej odvesny. Vezmeme si uhol \(FCM\). Protiľahlá odvesna k nemu má dĺžku \(\sqrt{3}\) a priľahlá odvesna je naša neznáma \(x\). Dostaneme rovnicu:

\[\tan(30^\circ) = \frac{\sqrt{3}}{x}.\]

Po úprave:

\[\begin{aligned} x &= \frac{\sqrt{3}}{\tan (30^\circ)},\\ x &= 3.\end{aligned}\]

Riešenie cez Pytagorovu vetu

Ak preklopíme trojuholník \(FMC\) v osovej súmernosti podľa úsečky \(MC\) na opačnú stranu, dostaneme trojuholník, ktorého základňa bude mať dvojnásobok dĺžky strany \(FM\), teda dĺžku \(2\cdot \sqrt{3}\). Uhol \(CFM\), ktorý ma \(60^\circ\), sa prenesie rovnako na druhú stranu. V tomto našom vzniknutom trojuholníku majú teda všetky uhly \(60^\circ\), takže trojuholník je rovnostranný. Z toho vyplýva, že aj strana \(FC\) má dĺžku \(2\cdot \sqrt{3}\) rovnako ako základňa. Keďže teraz poznáme dĺžky dvoch strán v pravouhlom trojuholníku \(FMC\), pomocou Pytagorovej vety si ľahko dopočítame aj tretiu stranu. Prepona \(FC\) má dĺžku \(2\cdot \sqrt{3}\) a odvesna \(FM\) dĺžku \(\sqrt{3}\). Dostaneme rovnicu:

\[\begin{aligned} |MC|^2 &= |FC|^2 - |FM|^2,\\ |MC|^2 &= (2\cdot\sqrt{3})^2 - (\sqrt{3})^2,\\ |MC|^2 &= 4\cdot 3 - 3,\\ |MC|^2 &= 9,\\ |MC| &= 3.\end{aligned}\]

Takže dĺžka časti \(x\) je teda \(3\) jednotky dĺžky a keďže máme také dve časti na strane tak náš rozdiel bude \(2\cdot x\), čo je \(6\). Rozdiel dĺžky strany väčšieho trojuholníka od dĺžky strany menšieho trojuholníka je \(6\) jednotiek dĺžky.