3. Konvexne Mysliaci Skalpel (κ ≤ 3) vzorové riešenie

Trojuholníkový lístok delíme na štyri časti ktoré budú medzi sebou zdieľať niektoré strany. Prvá vec, ktorú si potrebujeme uvedomiť, je, že dva konvexné útvary nemôžu mať spoločnú viac ako jednu stranu. Uvedomiť si, prečo je to tak, by nemal byť problém (ak neviete, zamyslite sa nad tým).

Táto informácia je celkom zaujímavá hneď pri šesťuholníku. Ten má šesť strán a niektoré z nich budú vnútri lístka, teda spoločné s inými mnohouholníkmi. V lístku budeme mať ešte tri ďalšie mnohouholníky, a s každým môže mať náš šesťuholník spoločnú najviac jednu stranu. Ostávajú nám tak tri strany ktoré nemôžu byť spoločné so žiadnym iným mnohouholníkom, musia teda ležať na vonkajšom okraji lístka. Trojuholníkový lístok má tri vonkajšie hrany a na každej môže ležať najviac jedna strana konvexného mnohouholníka. Toto nám nedáva veľmi na výber, v šesťuholníku máme šesť strán, najviac tri z nich môžu ležať na okraji lístka a najviac tri vo vnútri. Jeden zo spôsobov, ako to dosiahnuť, je umiestnenie dvoch jeho vrcholov do vnútra lístka, dvoch do vrcholov lístka, a dvoch na hrany lístka. Sú aj iné spôsoby umiestnenia, dostaneme pri nich však viac ako jeden kus zvyšku lístka o čom po ďalšom skúmaní zistíme, že neumožňuje splniť zadanie.

Poďme ďalej, na rade je päťuholník. Znovu môžu najviac tri jeho strany ležať vo vnútri lístka (kvôli zdieľaniu strán), a zároveň najviac dve ležať na okraji lístka (lebo lístok má tri hrany, ale jednu celú už zabral šesťuholník). Zase teda nemáme na výber a jeden vrchol päťuholníka musí ležať v poslednom vrchole lístka, dva musia ležať na hranách lístka (jeden z nich spoločný s šesťuholníkom) a dva vo vnútri lístka (jeden znovu spoločný s šesťuholníkom).

Kto by to čakal, dostávame sa k štvoruholníku, kde sa deje presne to isté. Najviac jedna strana leží na hrane lístka (už nám ostala len jedna voľná, aj to nie celá) a zvyšné tri musia ležať vo vnútri, dve z nich zdieľané s už existujúcimi mnohouholníkmi. Ostáva nám umiestniť už len trojuholník, a presne to je aj útvar ktorý nám na lístku zostal, máme teda hotovo.

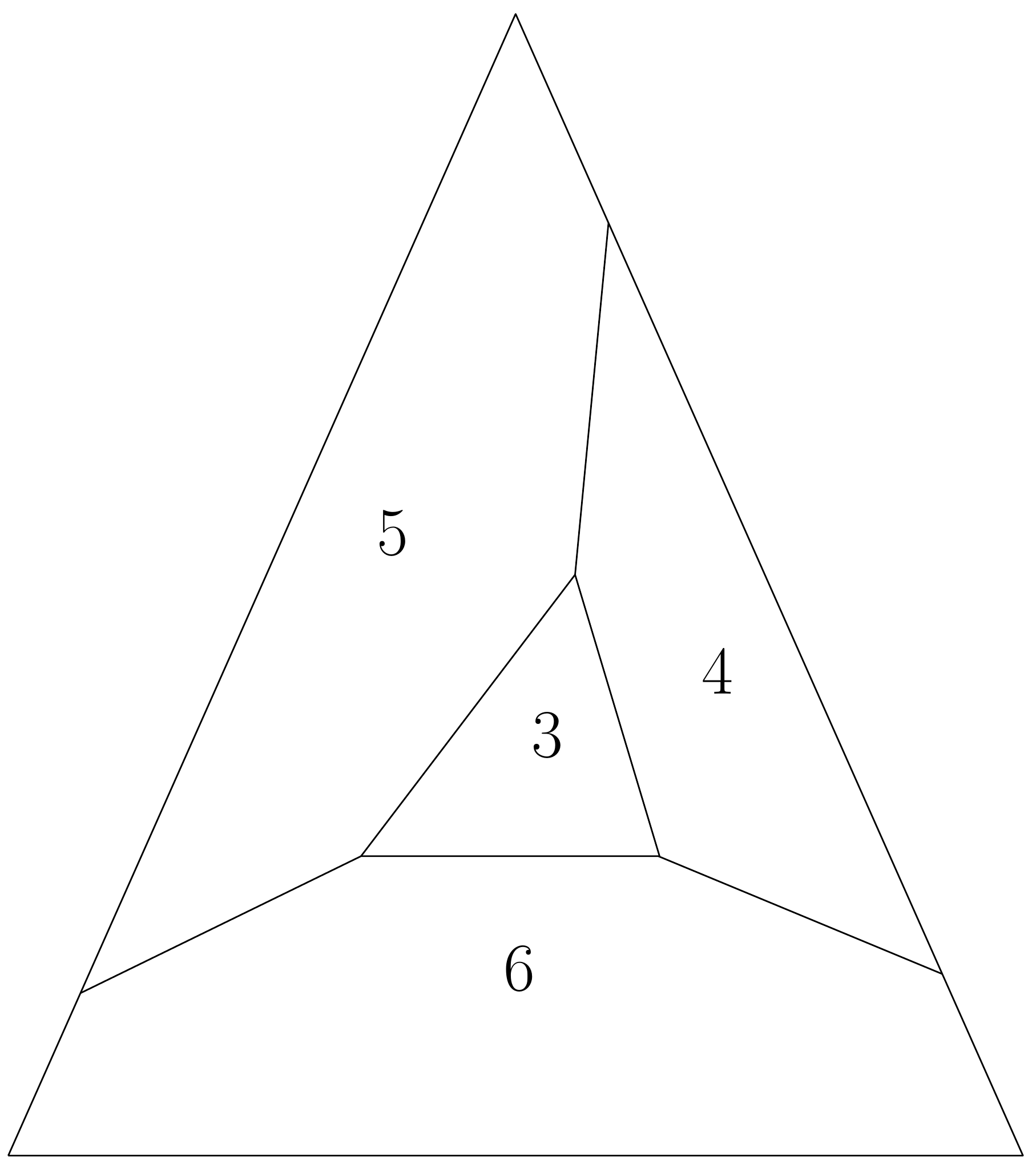
Nižšie môžete vidieť obrázok jedného možného riešenia, dostať sa k nemu sa dalo práve postupom z tohto vzoráku.