7. Kubisti Modelovali Siluety vzorové riešenie

Ukážeme si dva možné spôsoby riešenia tejto úlohy. Máme dokázať, že nejaký uhol je pravý, to spravíme napríklad tak, že sa ho pokúsime vyjadriť pomocou niektorých základných uhlov v rovnobežníku a uhlu \(PCB\). To sa však robí ťažšie, nakoľko si môžme všimnúť, že máme pracovať s polovičnými dĺžkami. Preto sa pokúsime nájsť fintu ako obídeme takéto zdĺhavé a nepríjemné vyjadrovanie uhlov. Známymi spôsobmi ako dostať polovičné dĺžky sú stredné priečky, rovnoľahlosť a určite mnohé ďalšie.

Riešenie cez strednú priečku.

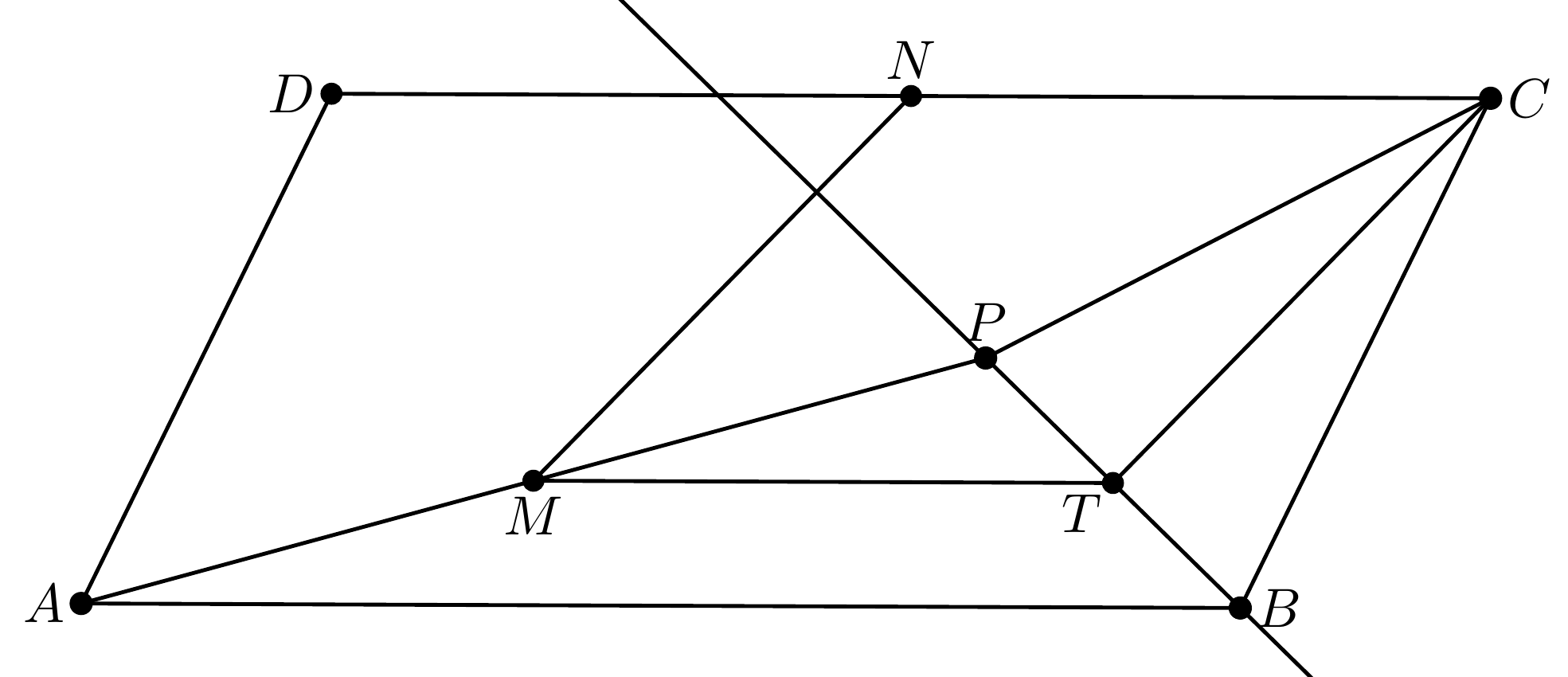
Tu sa dá vybrať viacero stredných priečok s ktorými vieme pracovať. Ak by sme napríklad vybrali strednú priečku \(ME\) tak sa dostaneme na riešenie cez rovnoľahlosť, ktoré je spomenuté nižšie. Mnohý z vás pracovali so strednou priečkou \(MT\), kde \(T\) je stred úsečky \(PB\), preto ju použijeme aj vo vzorovom riešení. Keďže trojuholník \(BCP\) je rovnoramenný tak \(TC\) je určite výška. Pripomeňme si, že platia tieto vzťahy: \(2\cdot|MT|=|AB|=|CD|=2\cdot|CN|\) a súčasne \(MT\parallel CN\) preto je \(MTCN\) rovnobežník. Keďže \(TC\perp PB\) tak z rovnobežnosti \(TC\) a \(MN\) platí aj \(PB \perp MN\). Čo sme chceli dokázať.

Riešenie cez rovnoľahlosť.

Keďže bod \(M\) je stredom úsečky \(AP\), dostávame prvú indíciu, kde rovnoľahlosť hľadať. Pozn. síce bod \(N\) je stredom \(DC\), ale rovnoľahlosť z bodu \(D\) alebo \(C\) by nám nepomohla uchopiť body \(M\) a \(P\), kdežto rovnoľahlosť v bode \(A\) alebo \(P\) sa nemusí zapodievať bodom \(N\) lebo je stredom úsečky \(CD\) a s tým sa nám dobre počíta. Skúsenejšie oko si všimne, že rovnoľahlosť z bodu \(A\) a koeficientom \(\frac{1}{2}\) je výhodnejšia ako rovnoľahlosť z bodu \(P\). Totiž bod \(P\) zobrazí do bodu \(M\), bod \(C\) zobrazí do bodu \(S\), čo je priesečník uhlopriečok, bod \(B\) zobrazí do bodu \(E\), stredu úsečky \(AB\), a zvyšné body nás nemusia trápiť, rozmyslite si prečo.

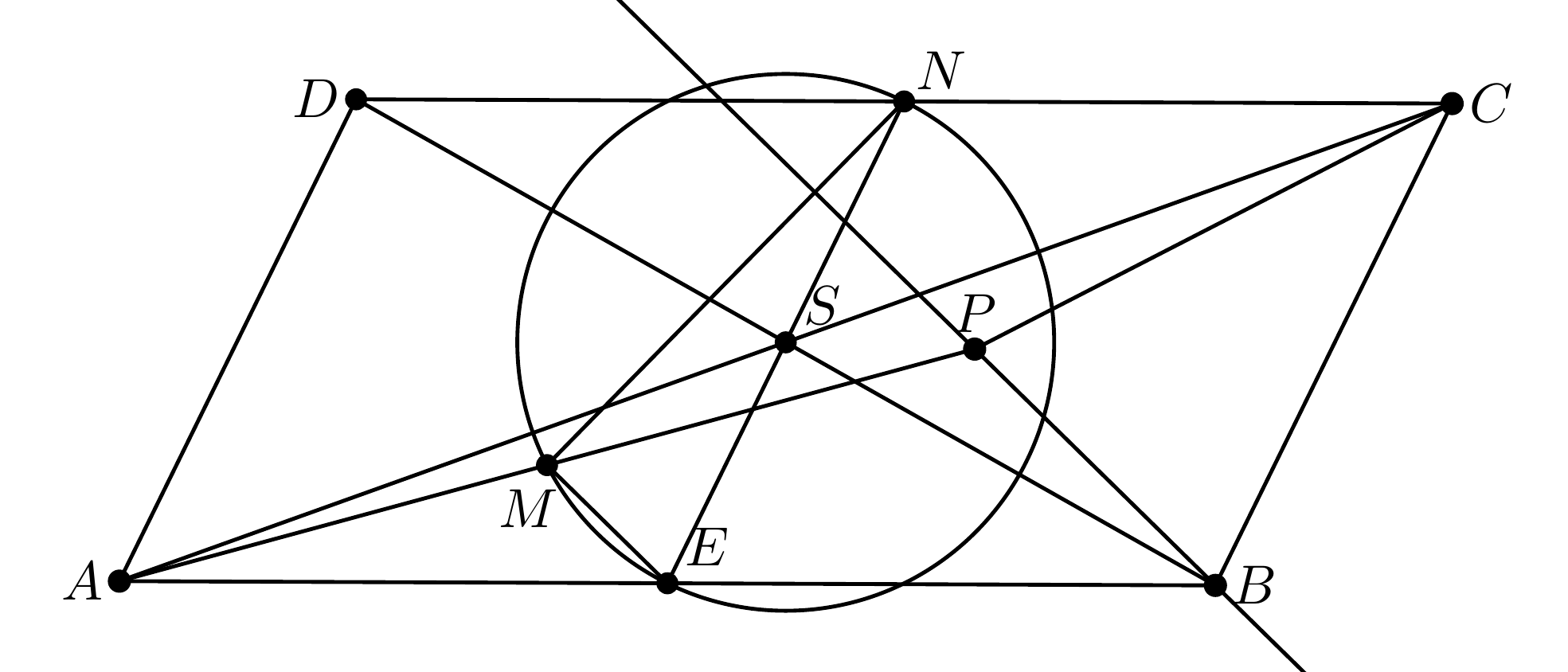
Keďže \(|PC|=|BC|\), tak po zobrazení bude platiť \(\frac{1}{2}\cdot|PC|=|MS|=|ES|\). Navyše, keďže \(S\) je priesečník uhlopriečok, tak \(|ES|=|SN|\), a teda kružnica so stredom v bode \(S\) prechádza bodmi \(N\), \(M\) a \(E\). Dokonca vieme, že \(EN\) je priemerom tejto kružnice pretože \(S\) leží v strede úsečky \(EN\). Preto obvodový uhol \(EMN\) má \(90^\circ\). Keďže rovnoľahlosť je podobné zobrazenie tak úsečky \(PB\) a \(ME\) sú rovnobežné, a preto uhol medzi priamkami \(PB\) a \(MN\) je \(90^\circ\).