Zadanie
Maťko po šokujúcich zisteniach Kiky a Joža o rovnobežiacich Dánoch a Belgičanov začal svoj výskum na Nemcoch. Štvoruholníku \(ABCD\), ktorému vieme vpísať kružnicu, platí navyše, že \(|AB| = |CD|\), \(|BC| < |AD|\) a strany \(BC\) a \(AD\) sú rovnobežné. Dokážte, že os uhla \(BCD\) rozpoľuje plochu štvoruholníka \(ABCD\).
Štvoruholník zo zadania si nakreslíme, a dostaneme nasledujúci obrázok:
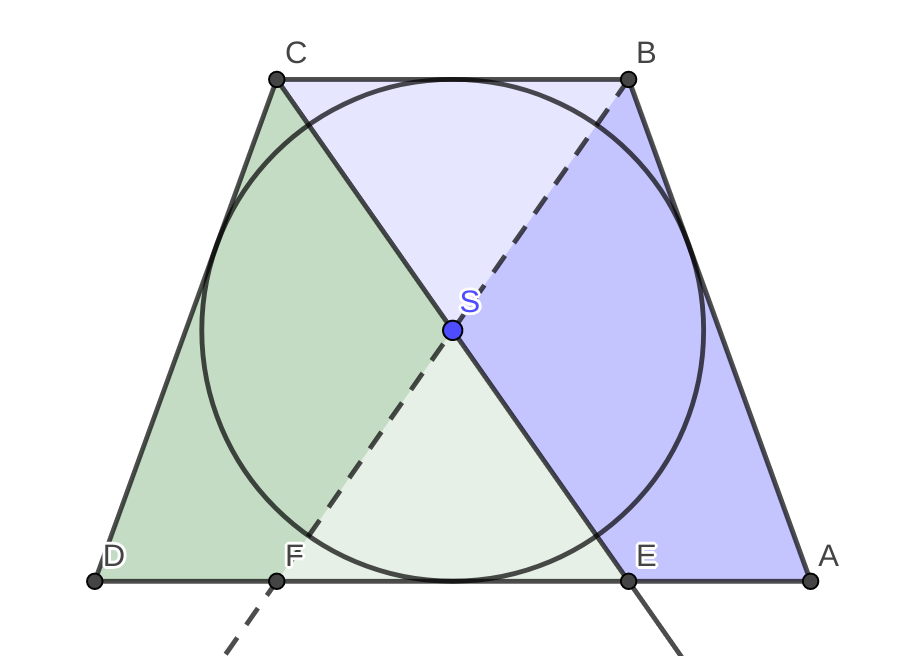
Aby sme naň mohli lepšie odkazovať, označme si stred vpísanej kružnice \(S\), ďalej priesečník osi uhla \(BCD\) a úsečky \(DA\) označíme \(E\), a vyznačme ešte os uhla \(ABC\) a jej priesečník s úsečkou \(DA\) označme \(F\).
Chceme ukázať, že trojuholník \(DEC\) (zelená) a štvoruholník \(EABC\) (modrá) majú rovnaký obsah.
Lichobežník, ktorý máme zo zadania, je rovnostranný. Preto uhly, pri vrcholoch \(A\) a \(B\) sú rovnaké ako uhly pri vrcholoch \(D\) a \(C\). Lichobežník je teda osovo symetrický. Preto aj os uhla \(ABC\) ho delí rovnako ako os \(BCD\). Keď máme nakreslené obe tieto osi a vieme že lichobežník je osovo symetrický, je ľahké všimnúť si, že štvoruholníky \(EABS\) (tmavomodrá) a \(DFSC\) (tmavozelená) majú rovnaký obsah. Keď sa teraz pozrieme na naše pôvodné oblasti, ktorých rovnosť chceme dokázať, a odmyslíme si tieto dva štvoruholníky, ostáva nám ukázať rovnosť obsahov trojuholníkov \(FES\) (bledomodrá) a \(SBC\) (bledozelená).
Bod \(S\) je v strede medzi rovnobežkami \(BC\) a \(AD\), a teda úsečky \(CE\) a \(BF\) delí na polovicu. Okrem toho, uhly \(CSB\) a \(ESF\) sú vrcholové, a teda majú rovnakú veľkosť. Z toho už vidíme, že naše trojuholníky sú zhodné, a teda majú rovnaký obsah.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.