Zadanie
Kika si kúpila poncho v tvare lichobežníka. Na lichobežníku \(ABCD\) so základňami \(AB\) a \(CD\) ležia na uhlopriečkach \(AC\) a \(BD\) po rade body \(P\), \(Q\) tak, že platí \(|\sphericalangle APD|\) = \(|\sphericalangle BQC|\). Ukažte, že platí \(|\sphericalangle AQD|\) = \(|\sphericalangle BPC|\).
Skúsme sa na začiatok úlohy odraziť od toho, čo vieme. Zo zadania platí: \(|\sphericalangle APD| = |\sphericalangle BQC|\). Vieme tiež ľahko odvodiť, že \(|\sphericalangle DPC| = |\sphericalangle DQC|\), keďže ide o susedné uhly s uhlami zo zadania.
Keď sa pozrieme na trojuholníky \(DPC\) a \(DQC\), zistíme, že majú rovnakú základňu \(DC\) a aj rovnakú veľkosť uhla oproti základni, teda pri vrcholoch \(P\) a \(Q\). Mali by sme spozornieť a uvedomiť si, čo nám to napovedá. Konkrétne to, že bodom \(P\), \(Q\), \(C\), \(D\) vieme opísať kružnicu a tieto dva uhly sú jej obvodovými uhlami (prislúchajúce základni \(DC\)).
Štvoruholníku \(PQCD\) sme vedeli opísať kružnicu a teda je tetivový. Nezabudnime, že pre tetivový štvoruholník platí, že súčet jeho protiľahlých uhlov je \(180^\circ\). Keďže základne lichobežníka \(AB\) a \(DC\) sú rovnobežné, vieme, že vďaka striedavosti uhlov platí \(|\sphericalangle BAC| = |\sphericalangle ACD|\). Rovnako platí \(|\sphericalangle ABD| = |\sphericalangle BDC|\).
Z toho, že štvoruholník \(PQCD\) je tetivový vieme, že \(|\sphericalangle PQD| = |\sphericalangle ACD|\).
Teraz ukážeme, že aj štvoruholník \(ABQP\) je tetivový. Chceli by sme, aby platilo \(|\sphericalangle CAB| + |\sphericalangle BQP| = 180^\circ\). \(|\sphericalangle BQP|\) môžeme vyjadriť pomocou jeho susedného uhla \(PQD\) ako \(180^\circ - |\sphericalangle PQD|\). Veľkosť \(|\sphericalangle PQD|\) a \(|\sphericalangle ACD|\) je rovnaká, tiež vďaka striedavým uhlom, vieme že \(|\sphericalangle PAB| = |\sphericalangle ACD|\) a teda \(|\sphericalangle BQP| = 180^\circ - |\sphericalangle PAB|\). Dokázali sme, že protiľahlé uhly v štvoruholníku \(ABQP\) majú súčet \(180^\circ\), čiže ide o tetivový štvoruholník. Z toho vyplýva, že vieme bodom \(A\), \(B\), \(P\), \(Q\) opísať kružnicu.
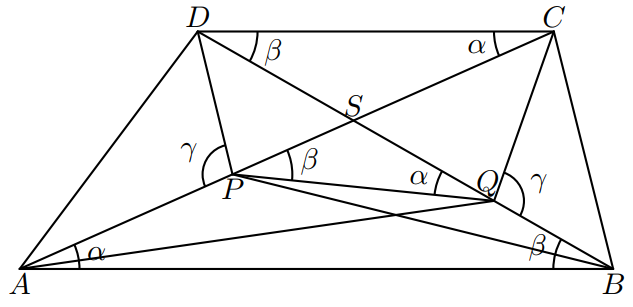
Trojuholníky \(ABP\) a \(ABQ\) majú rovnakú základňu \(AB\) a rovnakú veľkosť uhlov pri vrcholoch P a Q, keďže ide o obvodové uhly. Keďže majú rovnakú veľkosť, tak majú rovnakú veľkosť aj ich susedné uhly \(BPC\) a \(AQD\), čo bolo treba dokázať.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.