9. KMS Má SWAG! vzorové riešenie

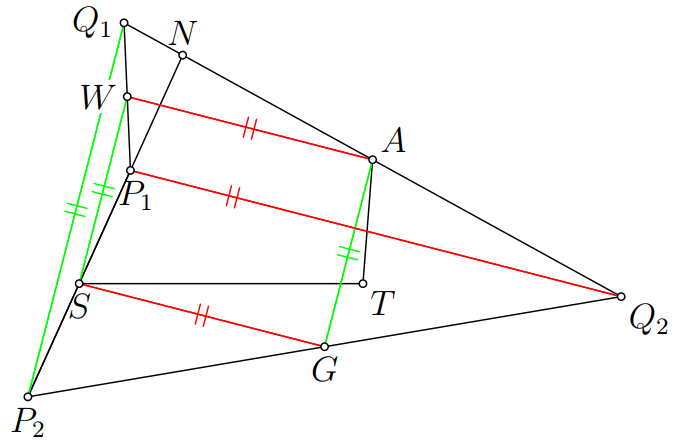
Môžeme si všimnúť, že v úlohe vystupuje dosť stredov: \(S\), \(W\), \(A\), \(G\) sú postupne stredy úsečiek \(P_2P_1\), \(P_1Q_1\), \(Q_1Q_2\), \(Q_2P_2\). Preto nám prídu vhod stredné priečky. V trojuholníku \(P_1P_2Q_1\) máme strednú priečku \(SW\), a preto je rovnobežná s úsečkou \(P_2Q_1\). Podobne, z trojuholníka \(Q_2P_2Q_1\) dostaneme, že stredná priečka \(AG\) je rovnobežná so stranou \(P_2Q_1\). Máme teda tri rovnobežky: \(SW\), \(AG\) a \(P_2Q_1\). Podobným spôsobom dostaneme tiež rovnobežky \(WA\), \(GS\), \(P_1Q_2\). Z toho vyplýva, že \(SWAG\) je rovnobežník. Aby sme ukázali, že to je obdĺžnik, stačí nám ukázať, že priamky \(P_2Q_1\) a \(P_1Q_2\) sú na seba kolmé.

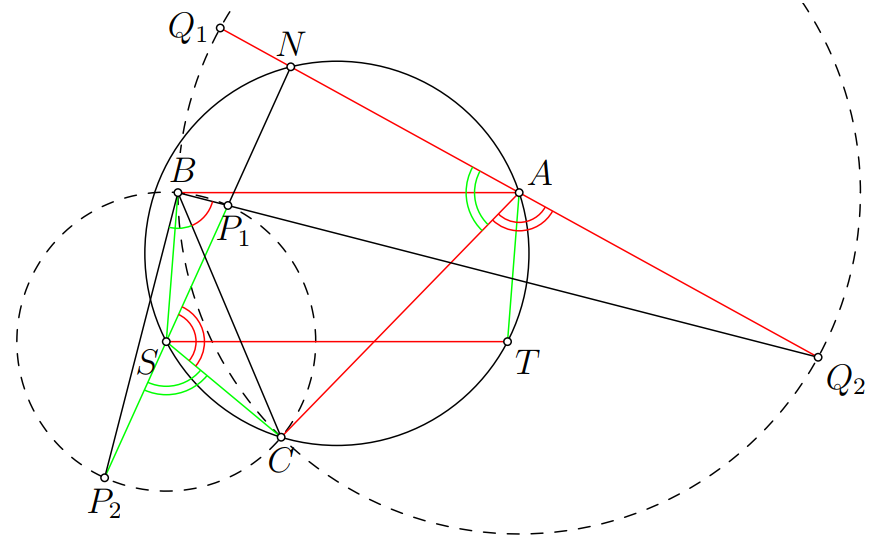
V zadaní máme veľa rovnakých dĺžok. Dobre sa s nimi pracuje, keď sú pokope. Zvoľme teda bod \(B\) tak, aby \(STAB\) bol rovnobežník. Ďalej, obraz bodu \(T\) v osovej súmernosti podľa osi strany \(SA\) označme \(C\). Zjavne bod \(C\) leží na kružnici opísanej tetivovému štvoruholníku \(STAN\). Dostali sme tak pekne pri sebe rovnaké dĺžky \(|SP_1| = |SP_2| = |SB| = |SC|\) a \(|AQ_1| = |AQ_2| = |AB| = |AC|\). Inými slovami, body \(P_1\), \(P_2\), \(B\), \(C\) ležia na kružnici \(k\) so stredom v \(S\) a body \(Q_1\), \(Q_2\), \(B\), \(C\) na kružnici \(l\) so stredom v \(A\). Tieto kružnice sú tálesovými nad priemermi \(P_1P_2\) a \(Q_1Q_2\).

Poďme zistiť veľkosť uhla \(P_2BQ_2\). Označme si \(|\sphericalangle NSC| = 2\alpha\). Z tetivového štvoruholníka \(SCAN\) máme \(|\sphericalangle CAN| = 180^\circ - 2\alpha\). Zas zo susedných uhlov máme \(|\sphericalangle P_2SC| = 180^\circ - 2\alpha\) a \(|\sphericalangle CAQ_2| = 2\alpha\). S využitím stredového a obvodového uhla v kružniciach \(k\) a \(l\) dostaneme \(|\sphericalangle P_2BC| = |\sphericalangle P_2SC|/2 = 90^\circ - \alpha\) a \(|\sphericalangle Q_2BC| = \alpha\). Dostávame tak, že \(|\sphericalangle P_2BQ_2| = |\sphericalangle P_2BC| + |\sphericalangle Q_2BC| = 90^\circ\). Body \(P_1\) a \(Q_2\) ležia na kolmici na úsečku \(P_2B\) v bode \(B\), preto body \(P_1\), \(Q_2\) a \(B\) ležia na jednej priamke. Podobne na jednej priamke ležia aj body \(P_2\), \(Q_1\), \(B\). Ako sme ukázali, tieto priamky zvierajú pravý uhol, čo dokazuje, že \(SWAG\) je obdĺžnik.

Ešte si na záver rozmyslime, že naše riešenie funguje pre každú konfiguráciu. Body, ktoré využívame totiž ležia vždy v správnej polohe.

Komentár

Ukázať, že priamky \(P_1Q_2\) a \(P_2Q_1\) sú na seba kolmé bolo možné mnoho ďalšími spôsobmi, s využitím iných uhlov. Pri niektorých si stačilo dokresliť len jeden z bodov \(B\), \(C\). Avšak pri mnohých spôsoboch si bolo treba dať pozor na konfigurácie bodov. Napr. rovnosť \(|\sphericalangle P_2BQ_2| = |\sphericalangle P_2BS| + |\sphericalangle SBA| + |\sphericalangle ABQ_2|\) neplatí pri každej konfigurácii bodov. Niekedy sa v nej zmenia niektoré znamienka plus na mínus.

Ukážeme ešte jedno riešenie, ktoré využíva špirálovú podobnosť a jej vlastnosti. Môžete si o nej prečítať od strany 22 v seriáli PraSe Geometrická zobrazení.

Iné riešenie

Uvažujme špirálovú podobnosť so stredom v bode \(C\), ktorá zobrazuje úsečku \(Q_2Q_1\) na \(P_1P_2\). Vieme, že jej stred \(C\) leží na druhom priesečníku kružníc opísaných trojuholníkom \(NP_1Q_2\) a \(NP_2Q_1\). Táto špirálová podobnosť zobrazuje aj bod \(A\) (stred \(Q_2Q_1\)) na bod \(S\) (stred \(P_1P_2\)). Preto jej stred \(C\) leží aj na kružnici opísanej trojuholníku \(SAN\). Z koeficientov tejto špirálovej podobnosti dostaneme \(|CA| : |CS| = |Q_2A| : |P_1S| = |AC| : |SC| = |ST| : |AT|\). Keď to spojíme s rovnosťou obvodových uhlov \(|\sphericalangle SCA| = |\sphericalangle STA|\), tak dostaneme, že trojuholníky \(SCA\) a \(ATS\) sú podobné. Keďže majú spoločnú stranu \(AS\), tak sú aj zhodné. Z toho dostávame, že \(C\) je totožný s bodom \(C\) z predchádzajúceho riešenie, teda leží na oboch tálesových kružniciach nad priemermi \(P_1P_2\) a \(Q_1Q_2\).

Keďže špirálová podobnosť chodí po dvoch, \(C\) je aj stred špirálovej podobnosti, ktorá zobrazuje úsečku \(P_1Q_2\) na \(P_2Q_1\). Jej uhol otočenia je \(|\sphericalangle P_1CP_2| = 90^\circ\). Preto sú úsečku \(P_1Q_2\) a \(P_2Q_1\) tiež na seba kolmé.