Zadanie
Slavo našiel v potoku starý televízor zapadnutý prachom. Všimol si, že do prachu na obrazovke sa dobre kreslí, tak si ihneď začal kresliť.
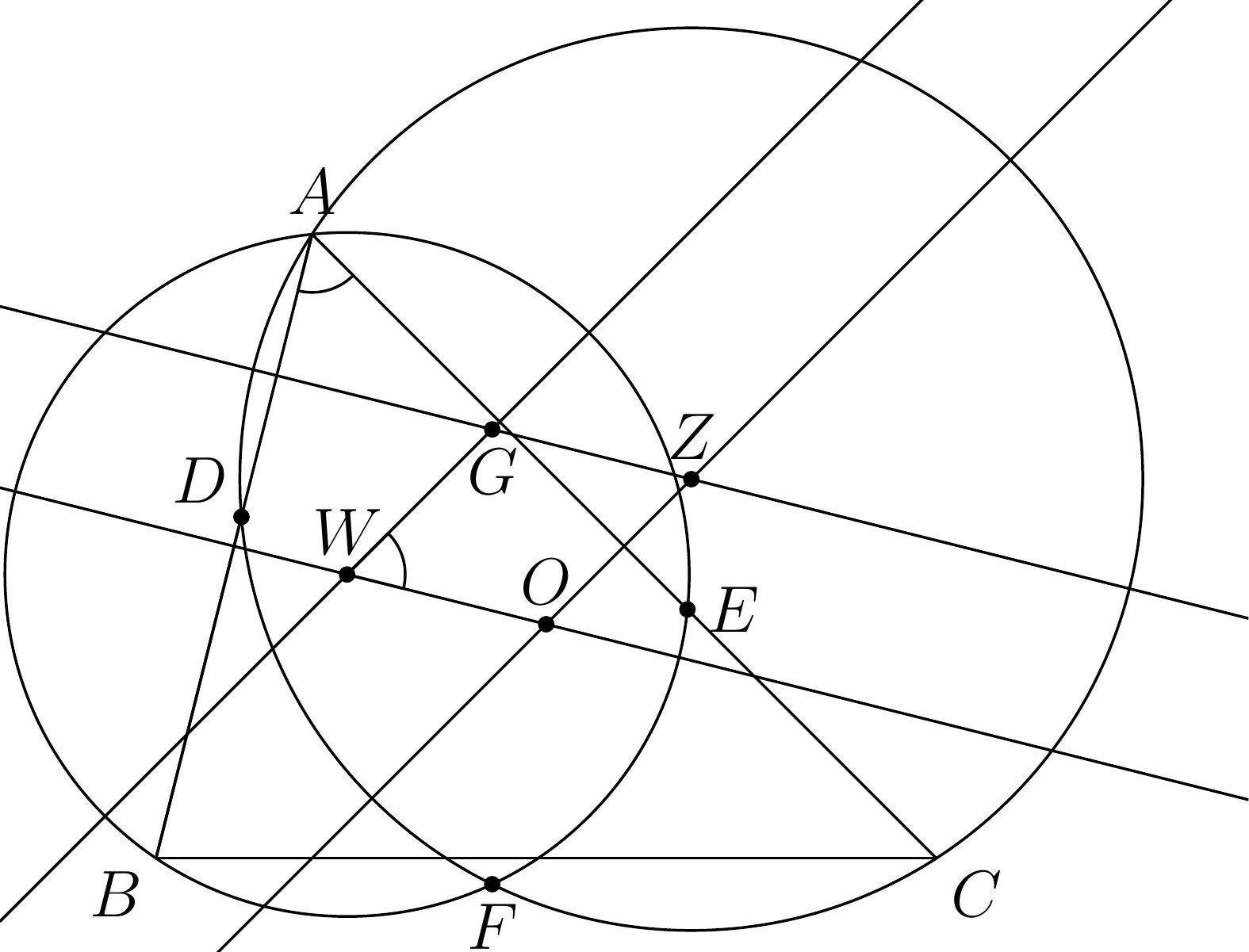
Na stranách \(AB\), \(AC\) trojuholníka \(ABC\) (\(|AB| \ne |AC|\)) ležia body \(D\), \(E\) tak, že \(|BD| = |CE|\). Druhý priesečník kružníc opísaných trojuholníkom \(ABC\) a \(ADE\) označme \(X\). Druhý priesečník kružníc opísaných trojuholníkom \(ABE\) a \(ACD\) označme \(Y\). Dokážte, že \(|\sphericalangle XAY| = 90^\circ\).
Najprv si ukážeme, že \(X\) je stred oblúku \(BC\) obsahujúceho \(A\).Tento bod nazývame \(\check{N}_A\), je to takzvaný Antišvrčkov bod v trojuholníku \(ABC\). Uvažujme trojuholníky \(\check{N}_ADB\) a \(\check{N}_AEC\). Strany \(\check{N}_AB\) a \(\check{N}_AC\) sú rovnako dlhé, a tiež strany \(DB\) a \(EC\) sú rovnako dlhé. Ďalej z tetivovosti \(A\check{N}_ABC\) vieme, že uhly medzi nimi (\(\sphericalangle DB\check{N}_A\) a \(\sphericalangle EC\check{N}_A\)) sú tiež rovnaké. Trojuholníky \(EC\check{N}_A\) a \(DB\check{N}_A\) sú zhodné, teda aj podobné. To ďalej implikuje podobnosť trojuholníkov \(CB\check{N}_A\) a \(ED\check{N}_A\), teda nakoľko bol uhol \(|\sphericalangle B\check{N}_AC|=\alpha\), je aj \(|\sphericalangle D\check{N}_AE|=\alpha\). Potom je ale štvoruholník \(A\check{N}_ADE\) tetivový. Teda naozaj platí, že \(\check{N}_A\) je priesečník kružníc \(ABC\) a \(ADE\). Teda \(\check{N}_A=X\). Všimnime si, že teraz nám stačí ukázať, že Y leží na osi uhla \(BAC\), pretože o bode \(X\) je známe, že leží na osi vonkajšieho uhla. 1
Tak ako na to? Môžeme napríklad uvažovať stredy \(Z\) a \(W\) kružníc opísaných trojuholníkom \(ADC\) a \(ABE\). Ideme si ukázať, že ich spojnica je kolmá na os uhla pri vrchole \(A\), pretože druhý priesečník je obrazom \(A\)-čka podľa priamky \(ZW\). A to nejak platí. Stačí si nám iba všimnúť, že ak sa pozrieme na rovnobežník tvorený osami úsečiek \(AB\), \(AD\), \(AC\), \(AE\), tak kvôli rovnosti \(|BD|=|EC|\) tie dvojice rovnobežných priamok budú mať rovnaké vzdialenosti. To ale práve znamená (premyslite si!), že je to kosoštvorec. To ale znamená, že trojuholník \(WOZ\) je rovnoramenný, s uhlom \(180^\circ-\alpha\) pri vrchole \(O\). Z toho plynie, že spojnica \(WZ\), ktorá je osou uhla pri vrchole \(W\) musí byť kolmá na os uhla \(BAC\), pretože ak otočíme ten kosoštvorec o \(90^\circ\), tak jeho strany budú práve rovnobežné so stranami \(AB\), \(AC\), pretože strany kosoštvorca sú osi úsečiek ležiacich na spomínaných priamkach \(AB\), \(AC\). To ale znamená, že aj otočením osi uhla pri vrchole \(W\) dostaneme niečo rovnobežné s osou uhla pri \(A\). A práve toto sme chceli ukázať, sme hotoví, \(AX\) a \(AY\) sú naozaj kolmé.
Viď napríklad https://mks.mff.cuni.cz/archive/36/uvod2s.pdf↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.