Zadanie
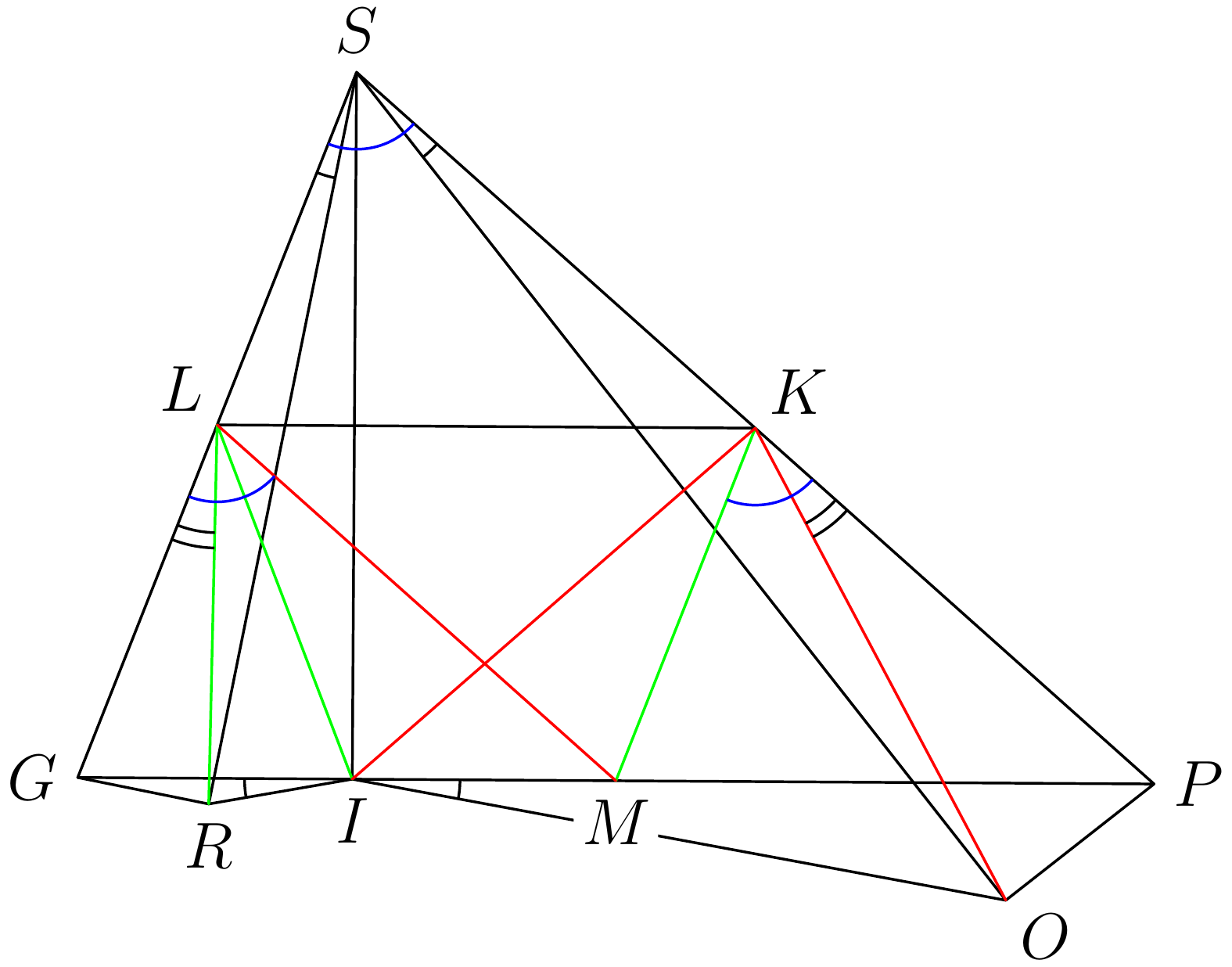
Miro sa stratil v Bermundskom ostrouhlom trojuholníku \(GPS\). Rozhodol sa použiť GPS, no tá v trojuholníku \(GPS\) funguje netriviálne. O svojej polohe sa dozvedel nasledovné: Bod \(M\) je stred strany \(GP\) a \(I\) je päta výšky na stranu \(GP\). Predpokladajme, že \(R\) a \(O\) sú body v opačnej polrovine danej priamkou \(GP\) než bod \(S\) také, že \(GR \perp SR\), \(PO \perp SO\) a \(|\sphericalangle PSO| = |\sphericalangle GSR|\). Dokážte, že Miro sa točí do kolečka, t. j. že \(MIRO\) je tetivový štvoruholník.
Označme si \(|\sphericalangle GSP| = \alpha\) a \(|\sphericalangle PSO| = |\sphericalangle GSR| = \phi\). Ďalej si označme stredy strán \(SP\) a \(SG\) postupne \(K\), \(L\). Vďaka pravým uhlom \(GRS\) a \(GIS\) ležia body \(S\), \(G\), \(R\), \(I\) na kružnici so stredom v bode \(L\). Podobne, body \(S\), \(P\), \(O\), \(I\) ležia na kružnici so stredom v bode \(K\). Vďaka obvodovým uhlom v týchto kružniciach máme \(|\sphericalangle GIR| = |\sphericalangle GSR| = \phi = |\sphericalangle PSO| = |\sphericalangle PIO|\). Z toho vidíme, že priamka \(GP\) je osou vonkajšieho uhla \(RIO\). Aby sme ukázali, že \(MIRO\) je tetivový štvoruholník, stačí nám ukázať, že bod \(M\) leží na osi strany \(RO\), teda že bod \(M\) je antišvrkom prislúchajúcim k bodu \(I\) v trojuholníku \(RIO\), ktorý leží na kružnici jemu opísanej.1
Keďže \(LM\) je stredná priečka trojuholníka \(GPS\), tak \(|LM| = |PS|/2 = |KS| = |KI|\). Analogicky tiež získame \(|KM| = |GS|/2 = |LS| = |LR|\). Ďalej z vlastností stredných priečok vieme, že \(|\sphericalangle GLM| = |\sphericalangle PKM| = \alpha\). Z obvodového a stredového uhla zas máme \(|\sphericalangle GLR| = 2\phi = |\sphericalangle PKO|\). Preto aj \(|\sphericalangle RLM| = \alpha - 2\phi = |\sphericalangle MKO|\). Dostávame tak, že trojuholníky \(RLM\) a \(MKO\) sú zhodné podľa vety sus. Preto \(|MR| = |MO|\), čo sme chceli dokázať.
Ďalšie riešenia
Skoro každý riešiteľ tejto úlohy mal iné riešenie. Preto sme vybrali hlavné myšlienky tých riešení, ktoré nám pripadali zaujímavé či poučné. V niektorých riešeniach sme vynechali zistenia z prvého odseku riešenia vyššie. Nasledovné riešenia využívajú geometrické zobrazenia. Pokiaľ ich nepoznáte, dočítate sa o nich v seriáli PraSe Geometrická zobrazení.
Nech \(G' = S_R(G)\) (takto budeme ďalej značiť obraz bodu \(G\) v stredovej súmernosti so stredom \(R\)) a \(P' = S_O(P)\). Trojuholník \(SGP'\) sa v otočení so stredom \(S\) o uhol \(2\phi\) zobrazí na trojuholník \(SG'P\). Preto priamky \(GP'\) a \(G'P\) zvierajú uhol \(2\phi\). Potom už len dopočítame, že \(|\sphericalangle RMO| = 180^\circ - (|\sphericalangle GMR| + |\sphericalangle PMO|) = 180^\circ - (|\sphericalangle GPG'| + |\sphericalangle PGP'|) = 180^\circ - 2\phi\).
Definujeme si bod \(L\) ako priesečník kružnice opísanej trojuholníku \(RIO\) a úsečky \(GP\) a ukážeme, že \(L \equiv M\).2 Rovnoramenné trojuholníky \(RLO\) a \(SKO\) sú podobné (uu), preto existuje špirálová podobnosť so stredom v bode \(O\), ktorá zobrazuje jeden na druhý. Keďže špirálová podobnosť „chodí po dvoch“, tak existuje aj špirálová podobnosť so stredom \(O\) zobrazujúca \(RS\) na \(LK\). Preto \(|\sphericalangle LKO| = |\sphericalangle RSO| = \alpha - 2\phi\) a \(|\sphericalangle LKP| = |\sphericalangle MKP| = \alpha\).
Označme \(A = S_R(S)\) a \(B = S_O(S)\). Rovnoramenné trojuholníky \(SGA\) a \(BPS\) sú podobné. Body \(O\), \(M\), \(R\) sú stredy spojníc zodpovedajúcich si bodov. Preto vďaka kĺzaniu je s nimi podobný aj trojuholník \(OMR\) a \(|\sphericalangle RMO| = 180^\circ - 2\phi\).
V úlohe sa dali nájsť aj ďalšie pekné kružnice:
Na priamkach \(SR\) a \(SO\) zvoľme postupne body \(X\) a \(Y\) tak, aby \(SR \perp XP\) a \(SO \perp YG\). Bod \(M\) leží na osiach rovnobežkových pásov \(GY\), \(PO\) a \(GR\), \(PX\). Dá sa ukázať, že \(M\) je stred kružnice opísanej štvoruholníku \(ROXY\). Ide to cez mocnosť bodu \(S\) k tejto kružnici alebo vyuhlením \(|\sphericalangle RYO| = |\sphericalangle RXO| = 90^\circ - \phi\).
Napokon, ukázať tetivovosť štvoruholníka \(MIRO\) bolo možné cez to najpriamočiarejšie kritérium – ukázať, že sa osi jeho strán pretínajú v jednom bode, teda, že existuje bod, ktorý má od všetkých jeho vrcholov rovnako ďaleko. Dajte si však pozor, takýto prístup moc často nefunguje :).
Bodmi \(L\) a \(K\) prechádzajú postupne osi úsečiek \(IR\) a \(IO\), ktoré sa pretínajú v bode \(X\). Možno ukázať, že \(LKX\) je rovnoramenný trojuholník. Preto bodom \(X\) prechádza os úsečky \(LK\), ktorá je totožná s osou úsečky \(MI\) (\(MILK\) je rovnoramenný lichobežník).
Je známa vec, že v trojuholníku \(ABC\) sa os vonkajšieho uhla pri vrchole \(A\) a os strany \(BC\) pretínajú na opísanéj kružnici – dokážte si to! Tento ich spoločný bod sa neoficiálne nazýva antišvrkom. Viac si môžete o ňom prečítať na na str. 34 v seriáli PraSe Geometrie trojuholníka.↩
Takéto preformulovanie úlohy je celkom vhodné a pomôže aj pri iných prístupoch riešenia. Lepšie sa pri riešení využíva kružnica ako stred strany.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.