Zadanie
Kmeň Majestátnych saván má na svojom rituálnom oltári nakreslenú magickú hviezdu. Vždy pri ich rituáli do jej políčok vpisuje šaman čísla podľa posvätných podmienok.
Do každého políčka hviezdy treba vpísať jedno kladné celé číslo. Každé dve susedné políčka (tie, ktoré sú spojené čiarou) musia obsahovať čísla, ktoré majú najväčšieho spoločného deliteľa väčšieho ako \(1\). Každé dve nesusedné políčka musia obsahovať čísla, ktoré majú najväčšieho spoločného deliteľa \(1\). Koľko najmenej rôznych čísel možno použiť na vyplnenie hviezdy?
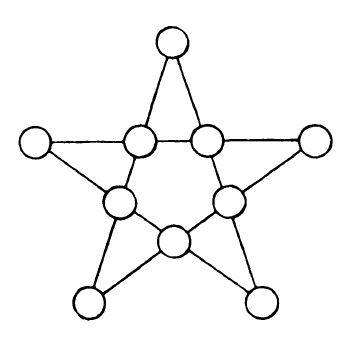
Na obrázku vidíme \(10\) políčok, do ktorých treba vpísať číslo. Najprv sa zamyslime nad tým, či sa vôbec dá obrázok vyplniť desiatimi číslami. Po chvíľke skúšania prídeme na to, že obrázok sa vyplniť dá. Napríklad tak, ako vidíme na obrázku (ktorý nám nakreslil Viktor Balan). Všimnime si, že sme nepoužili číslo \(1\). Nemôže tam byť preto, lebo by toto políčko nemalo najväčšieho spoločného deliteľa so svojimi susedmi, ktorý by bol väčší ako \(1\).
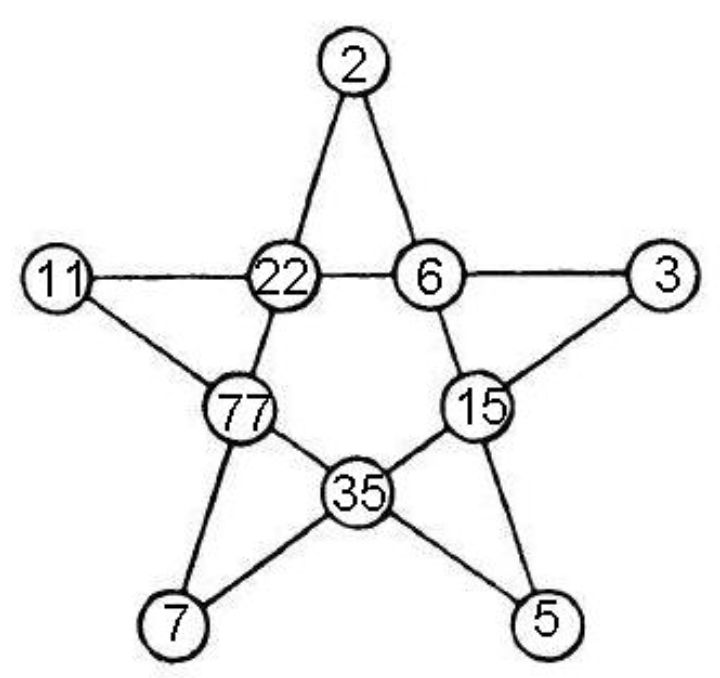
Teraz sa zamyslime nad tým, či by sa dal obrázok vyplniť aj s menším počtom čísel. To by znamenalo, že aspoň dvakrát doň napíšeme rovnaké číslo, označme si ho ako \(n\). Vieme o ňom, že je väčšie ako \(1\). Môžeme ho napísať na dve políčka, ktoré spolu nesusedia? Nemôžeme, lebo potom by tieto dve políčka mali najväčšieho spoločného deliteľa väčšieho ako \(1\) – obe sú predsa deliteľné číslom \(n\).
Môžu byť rovnaké čísla na susediacich políčkach? Mohli by, ale iba vtedy, keby tieto políčka mali tých istých susedov. Z obrázku vidíme, že také dve políčka tam nie sú. Ak existuje aspoň jedno ďalšie políčko, ktoré susedí iba s jedným z nich, nastane problém. Predstavme si, že namiesto \(6\) a \(22\) v obrázku dáme číslo \(n\). Políčko, na ktorom je teraz \(15\), potom musí byť súdeliteľné s číslom \(n\), ktoré s ním priamo susedí. Zároveň musí byť toto políčko nesúdeliteľné s druhým políčkom s číslom \(n\), ktoré s ním nesusedí. Takže ani na dve susedné políčka sa nedá napísať rovnaké číslo.
Najmenší počet čísel, čo potrebujeme na vyplnenie obrázka, je \(10\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.