Zadanie
Keď sa Jane dokochala kvetinovým záhonom, tak našla ešte niečo lepšie – Tarzana. Ten jej vravel:
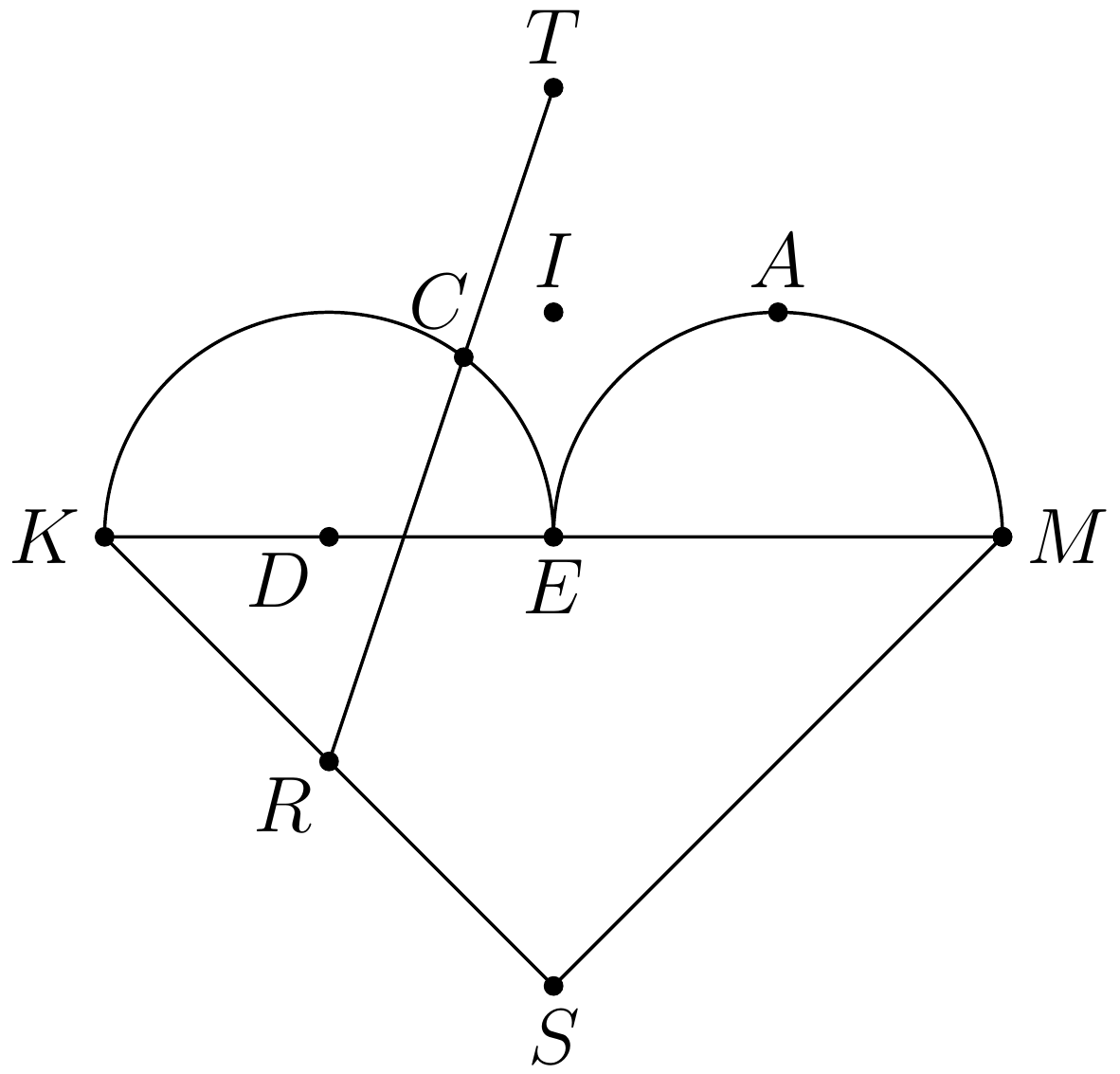
Kúsok Môjho Srdca je tvorený rovnoramenným trojuholníkom \(KMS\) s pravým uhlom pri vrchole \(S\). Bod \(E\) je stred strany \(KM\). Polkružnice v opačnej polrovine ku \(KMS\) nad priemermi \(KE\) a \(EM\) označme postupne \(k\), \(m\). Vyznačme si v Kúsku Môjho Srdca nasledujúce body:
Bod \(T\) je obraz bodu \(S\) v stredovej súmernosti so stredom v bode \(E\).
Bod \(R\) je stred strany \(KS\).
Bod \(D\) je stred úsečky \(KE\).
Bod \(C\) je priesečník priamky \(RT\) a polkružnice \(k\).
Bod \(I\) je stred úsečky \(ET\).
Bod \(A\) leží v polovici polkružnice \(l\).
Dokážte, že sedemuholníku \(SRDCIAM\) možno opísať kružnicu.
Riešiť túto úlohu sa dá viacerými spôsobmi. Dokázať, že jednotlivé body ležia na kružnici sa dá viacerými spôsobmi. Môžeme dokázať, že nejaký štvoruholník je obdĺžnik a teda sa mu dá opísať kružnica. (Stred kružnice je priesečník uhlopriečok a polomer je polovica dĺžky uhlopriečky.) Môžeme dokázať, že súčet protiľahlých uhlov v štvoruholníku je \(180^\circ\), a teda je to tetivový štvoruholník. Môžeme dokázať, že dva uhly, ktoré sa pozerajú na tú istú úsečku sú zhodné, sú to obvodové uhly nad tou úsečkou a teda ležia tieto štyri body na jednej kružnici. Môžeme nájsť niekde mocnosť bodu ku kružnici. V tomto riešení použijeme všetky vyššie spomenuté postupy. Existujú aj iné postupy, ktoré sú správne. Dá sa aj skromnejší počet týchto dokazovacích zbraní využiť. No poďme na to!
Trojuholník \(KMS\) je rovnoramenný a pravouhlý s pravým uhlom pri vrchole \(S\). Z toho vieme, že \(|\sphericalangle KMS|=45^\circ\). Úsečka \(ME\) je priemer kružnice \(m\) (resp. \(l\), zadanie sa rozhodlo značiť túto kružnicu oboma spôsobmi. Za vzniknuté komplikácie sa ospravedlňujeme.) Bod \(A\) leží na tejto Tálesovej kružnici, preto \(|\sphericalangle EAM|=90^\circ\). Nakoľko je bod \(A\) v polovici polkružnice \(m\), tak trojuholník \(EAM\) je rovnoramenný. Preto je \(|\sphericalangle AME| = 45^\circ\). Veľkosť uhla \(AMS\) vieme dorátať ako \(|\sphericalangle AMS|=|\sphericalangle AME|+|\sphericalangle KMS|=45^\circ + 45^\circ = 90^\circ\). Ak ešte dokážeme, že bod \(E\) leží na úsečke \(RA\), tak dostaneme obdĺžnik \(SMAR\). Tento štvoruholník totiž má tri pravé uhly, z čoho už musí byť obdĺžnikom. Z trojuholníka \(EMA\) vieme, že \(|\sphericalangle MEA| = 45^\circ\). Keďže je trojuholník \(KMS\) rovnoramenný, tak výška na základňu je taktiež ťažnica a taktiež osou uhla \(KSM\). Z toho vieme, že \(|\sphericalangle SEM| = 90^\circ\) a \(|\sphericalangle ESM| = 45^\circ\). Úsečka \(RE\) je strednou priečkou, čiže je rovnobežná s \(SM\). Uhly \(RES\) a \(ESM\) sú striedavé, teda sú zhodné a ich veľkosť je \(45^\circ\). Dopočítame veľkosť uhla \(REA\): \(|\sphericalangle REA|= |\sphericalangle RES| + |\sphericalangle SEM| + |\sphericalangle MEA| = 45^\circ + 90^\circ + 45^\circ = 180^\circ\). Teda \(REA\) je naozaj jedna úsečka a štvoruholník \(SMAR\) je obdĺžnik. Vieme už, že body \(S\), \(R\), \(A\), \(M\) ležia na kružnici.
Úsečka \(RD\) je strednou priečkou v trojuholníku \(KES\). Preto platí, že úsečky \(RD\) a \(SE\) sú rovnobežné. Úsečka \(SE\) je kolmá na \(KM\), pretože trojuholník \(KMS\) je rovnoramenný, teda \(SE\) je nielen ťažnicou ale i výškou. Potom je \(RD\) kolmá na \(KS\), resp. \(|\sphericalangle RDM| = 90^\circ\). Vidíme, že súčet protiľahlých uhlov je \(90^\circ + 90^\circ = 180^\circ\). Z čoho vieme, že štvoruholník \(SRDM\) je tetivový. Vieme už, že body \(S\), \(R\), \(D\), \(A\), \(M\) ležia na kružnici.
Pozrime sa teraz na trojuholník \(DIE\). Keďže \(SE\) je výška v trojuholníku \(KMS\), tak \(|\sphericalangle SEM| = 90^\circ\). Tento uhol je vrcholový s uhlom \(DEI\), z čoho vyplýva \(|\sphericalangle DEI| = 90^\circ\). Trojuholník \(KES\) je tiež rovnoramenný a pravouhlý, pretože má pravý uhol pri vrchole \(E\) a zvyšné dva uhly zhodné s veľkosťou \(45^\circ\). Teda \(|KE| = |ES|\). Nakoľko bod \(T\) je súmerný s bodom \(S\) v stredovej súmernosti podľa \(E\), tak aj \(|TE| = |ES|\). Keď znalosti z posledných dvoch spomenutých rovností spojíme, tak získame, že \(|TE| = |KE|\). Keďže body \(D\) a \(I\) sú stredy úsečiek \(KE\) a \(TE\), tak aj \(|DE| = |IE|\). Trojuholník \(DIE\) je rovnoramenný a pravouhlý. Odkiaľ vieme, že \(|\sphericalangle DIE| = 45^\circ\). Uhol \(DIE\) je taktiež uhlom \(DIS\) a uhol \(KMS\) je taktiež uhlom \(DMS\). Uhly \(DIS\) a \(DMS\) sú zhodné a oba sa pozerajú na \(DS\), teda sú to obvodové uhly. Preto body \(S\), \(D\), \(I\), \(M\) ležia na jednej kružnici. Vieme už, že body \(S\), \(R\), \(D\), \(I\), \(A\), \(M\) ležia na kružnici.
Už len bod \(C\) nám chýba. Keďže \(RD\) je stredná priečka, tak \(|RD| = \frac{1}{2} \cdot |SE| = \frac{1}{2} \cdot |KE| = |KD|\). Bod \(D\) je stredom kružnice \(k\). Body \(K\) a \(R\) sú rovnako vzdialené od bodu \(D\), preto bod \(R\) leží na kružnici \(k\) (polkružnici \(k\) doplnenej na kružnicu). Úsečka \(ST\) je dotyčnica k tejto kružnici, pretože \(|\sphericalangle DES| = 90^\circ\). Z mocnosti 1 bodu \(T\) ku kružnici \(k\) máme \(|TC| \cdot |TR| = |TE|^2\). Uhol \(EMT\) je vnútorným uhlom rovnoramenného pravouhlého trojuholníka \(EMT\). Bod \(A\) leží na úsečke \(MT\), pretože \(|\sphericalangle EMT| = 45^\circ\) aj \(|\sphericalangle EMA| = 45^\circ\) (a sú v rovnakej polrovine). Z mocnosti bodu \(T\) ku kružnici \(m\) máme \(|TA| \cdot |TM| = |TE|^2\). Platí, že \(|TC| \cdot |TR| = |TA| \cdot |TM|\), preto tieto štyri body musia byť na jednej kružnici (inak by k nim bod \(T\) nemal rovnakú mocnosť). Vieme už, že body \(S\), \(R\), \(D\), \(C\), \(I\), \(A\), \(M\) ležia na kružnici.
Ak nie si kamarát s mocnosťou bodu ku kružnici, tak máš aj inú možnosť ako plakať do vankúša, že ja ten bod \(C\) neviem dokázať. Môžeš spraviť napríklad toto: Najprv dokážeme, že \(KSMT\) je štvorec a bod \(A\) je v strede \(TM\) (dokáž si!). Potom uhly \(TRA\) a \(ARM\) sú zhodné, pretože trojuholníky \(TRA\) a \(MRA\) sú zhodné (napr. lebo \(|RA|=|RA|, |TA|=|MA|\) a uhol pri \(A\) je pravý). Bod \(D\) je stredom kružnice \(k\), pretože \(KE\) je priemer a bod \(D\) je v strede \(KE\). Už spomínaný uhol \(TRA\) je obvodovým uhlom nad oblúkom \(CE\), teda je polovičný oproti stredovému uhlu \(CDE\). Uvedomme si, že tento uhol \(CDE\) je aj uhol \(CDM\). Veľkosť uhla \(CDM\) je teda \(2 \cdot |\sphericalangle TRA|= |\sphericalangle TRA|+|\sphericalangle ARM|=|\sphericalangle CRM|\). Vidíme, že nad oblúkom \(CM\) máme dva rovnako veľké uhly (\(CDM\) a \(CRM\)), a teda sú to obvodové uhly a teda body \(R\), \(D\), \(C\), \(M\) sú na kružnici. Vieme už, že body \(S\), \(R\), \(D\), \(C\), \(I\), \(A\), \(M\) ležia na kružnici.
O mocnosti bodu ku kružnici sa dá dozvedieť viac od v zbierke KMS od strany 37:↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.