10. Krajiny Moje Svadobno-cestové vzorové riešenie

Predslov

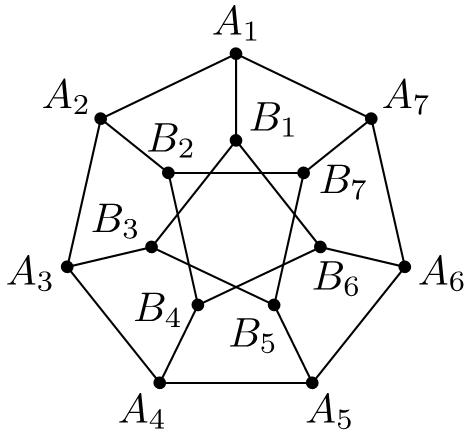
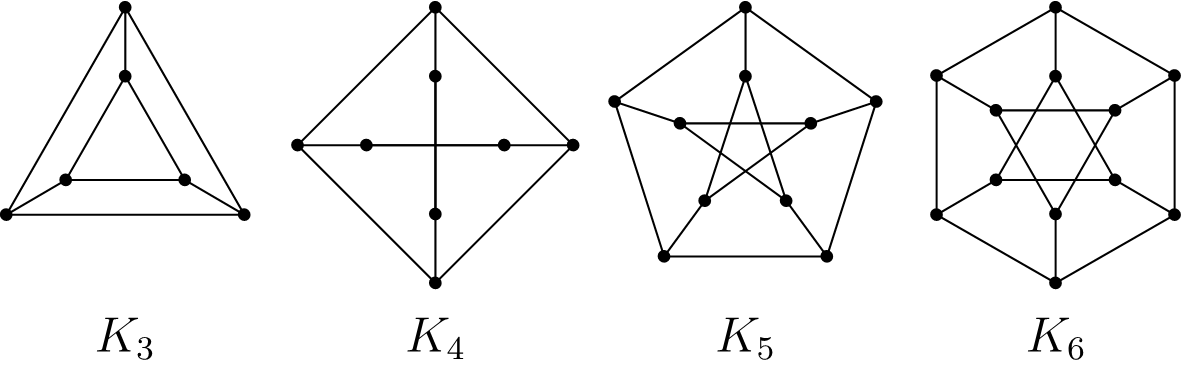
Najskôr sa poďme prehrýzť tým, ako sú mestá pospájané. Prvá odrážka je pomerne jasná. Aby sme zistili, čo hovorí druhá, je dobré skúsiť si nájsť všetky vyhovujúce dvojice \(i\), \(j\) opísané danou podmienkou (kľudne aj vyskúšaním všetkých možností). Keď to spravíme, zistíme, že sú vlastne spojené mestá \(A_1\) a \(A_2\), \(A_2\) a \(A_3\), …, \(A_{n-1}\) a \(A_n\), \(A_n\) a \(A_1\). Teda \(A\)-čkové mestá sú pospájané do kruhu. Podobne, keď si \(B\)-čkové mestá usporiadame do kruhu, tak letecké linky budú lietať ob mesto ďalej, teda medzi \(B_1\) a \(B_3\), \(B_2\) a \(B_4\), …, \(B_{n-1}\) a \(B_1\), \(B_n\) a \(B_2\). Preto jedným pekným spôsobom, ako si môžeme kresliť takéto krajiny je nakresliť si mestá typu \(A\) do vonkajšieho kruhu a mestá typu \(B\) do vnútorného kruhu. Krajinu \(K_7\) môžeme vidieť na obrázku 1 a niekoľko ďalších malých krajín (už bez označenia miest) na obrázku 2.

Táto úloha je do istej miery pekne hravá, aspoň tá časť, ktorá zahŕňa hľadanie okružných ciest v tých krajinách, v ktorých ide spraviť. Treba skúšať, všímať si a hľadať pekné vzory. Dosť nám pri tom pomôže to, že z každého mesta lietajú práve tri linky. Preto práve dve z nich budú použité v okružnej ceste a práve jedna z nich bude nepoužitá. Keď nájdeme nejakú nepoužitú linku, tak vieme, že všetky ostatné linky, ktoré lietajú z jej dvoch koncových miest musia byť použité. Taktiež linka musí byť nepoužitá, keď by sme s jej použitím dostali okruh, ktorý neprechádza všetkými mestami. Takéto a podobné úvahy nám môžu značne pomôcť pri hľadaní okružných ciest.

Takýmto skúšaním možno prísť na to, že okružnú cestu možno spraviť vo všetkých krajinách \(K_n\), v ktorých \(n\) nie je tvaru \(6k + 5\). Príklady okružných ciest v niektorých malých krajinách sú znázornené na obrázku 3.

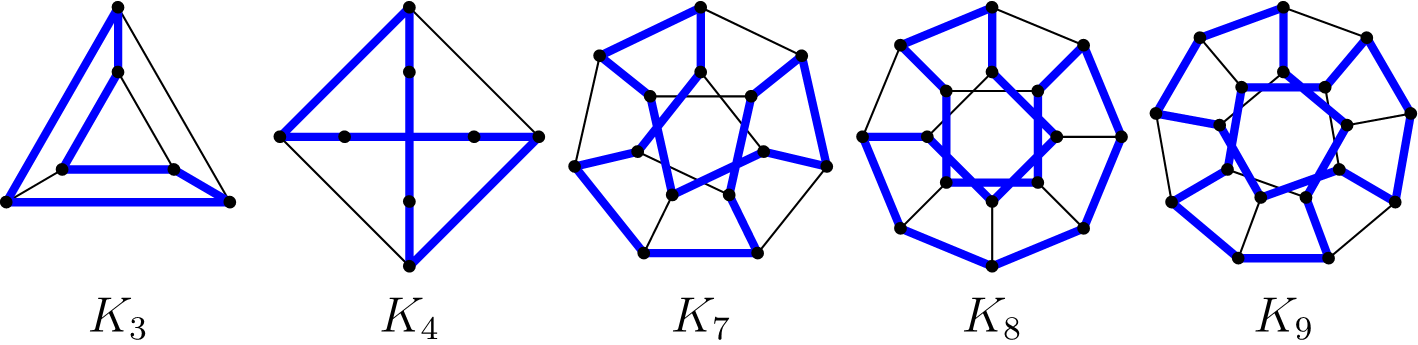
V našom vzorovom riešení najprv opíšeme okružné cesty v týchto krajinách. Potom ukážeme, že pre \(n = 6k + 5\) nemožno spraviť v krajine \(K_n\) okružnú cestu. V celom našom riešení budeme indexy miest brať vždy modulo \(n\). To znamená, že keď niekde napíšeme mesto \(X_i\) (\(X \in \{A, B\}\)) s indexom \(i\) mimo rozsahu \(1,\, 2,\, \dots,\, n\), tak tým myslíme mesto \(X_j\), pre ktoré index \(j\) dáva po delení číslom \(n\) rovnaký zvyšok ako \(i\). Napríklad \(A_{2n+1} = A_1\), \(A_{-3} = A_{n-3}\).

Konštrukcie

Nájsť okružnú cestu pre párne \(n\) je azda najjednoduchšie. Zjavne stačí prejsť mestami v poradí \[A_1,\ A_2,\ B_2,\ B_4,\ \dots,\ B_{n-2},\ B_{n},\ A_{n},\ A_{n-1},\ \dots,\, A_4,\, A_3,\, B_{3},\ B_{5},\ \dots,\ B_{n-1},\ B_{1},\ A_{1}.\]

Pre \(n = 6k + 3\), kde \(k \ge 1\), spravíme nasledovnú okružnú cestu:

• Prechádzame mestami \(A_{6i+1},\ A_{6i+2},\ A_{6i+3},\ B_{6i+3},\ B_{6i+5},\ B_{6i+7}\) pre \(i\) postupne rovné \(0,\, 1,\, \dots,\, k - 1\).

• Ďalej prejdeme mestami \(A_{6k + 1},\, A_{6k + 2},\, A_{6k + 3},\, B_{6k + 3},\, B_2,\, B_4\), čím sa dostaneme opäť k malým indexom.

• Ešte raz prehádzame v smere rastúcich indexov mestami \(A_{6i + 4},\, A_{6i+5},\, A_{6i+6},\, B_{6i+6},\, B_{6i+8},\, B_{6i+10}\) pre \(i\) postupne rovné \(0,\, 1,\, \dots,\, k - 1\). Skončíme tak v meste \(B_{6k + 4} = B_1\), z ktorého sa vrátime späť do mesta \(A_1\), kde sme začali.

Konštruckiu pre \(n = 3\) sme uviedli na obrázku 3 Pre \(n = 6k + 1\), kde \(k \ge 1\), spravíme nasledovnú okružnú cestu:

• Začneme najskôr s mestami \(A_5,\ A_4,\ A_3,\ B_3,\ B_1,\ A_1,\ A_2,\ B_2,\ B_4,\ B_6\).

• Potom prechádzame mestami \(A_{6i},\ A_{6i+1},\ A_{6i+2},\ B_{6i+2},\ B_{6i+4},\ B_{6i+6}\) pre \(i\) postupne rovné \(1,\, 2,\, \dots,\, k-1\).

• Následne prejdeme mestami \(A_{6k},\ A_{6k+1},\ B_{6k+1},\ B_{6k-1}\), čím sa otočíme.

• Pokračujeme späť v opačnom smere \(A_{6i+5},\ A_{6i+4},\ A_{6i+3},\ B_{6i+3},\ B_{6i+1},\ B_{6i-1}\) pre \(i\) postupne rovné \(k-1,\, k-2,\, \dots,\, 1\).

Všetky opísané postupnosti miest sú zjavne okružnými cestami.

Nevyhovujúce krajiny

Ostávajú má už len \(n = 6k + 5\), o ktorých ukážeme, že v nich nie je možné spraviť okružnú cestu. Začneme s najmenším prípadom \(n = 5\). Krajina \(K_5\) je pekne symetrická, preto môžeme celkom ľahko prebrať všetky možnosti. BUNV (bez ujmy na všeobecnosti) okružná cesta pôjde linkou \(B_1A_1\) a stále si môžeme BUNV povedať, že pokračuje linkou \(A_1A_2\). Z toho dostávame, že linka \(A_1A_5\) nebude použitá. Preto musia byť použité linky \(B_5A_5\) a \(A_5A_4\). Ak by linka \(A_3B_3\) nebola použitá, tak by musela byť použitá každá z liniek \(A_2A_3\), \(A_3A_4\), \(B_1B_3\), \(B_3B_5\), čím by sa nám použité linky uzavreli skôr ako by prešli všetky mestá. Preto musí byť linka \(A_3B_3\) použitá. Dostali sme sa opäť do symetrickej situácie, preto si BUNV môžeme povedať, že použitá je linka \(A_2A_3\). Potom linka \(A_3A_4\) je nepoužitá, teda \(A_4B_4\) je použitá. Aby sme nedostali kratšiu okružnú cestu, tak aj linka \(B_1B_3\) je nepoužitá. Preto sú použité linky \(B_1B_4\) a \(B_3B_5\). Dostali sme tak opäť okružnú cestu, ktorá vynechala jednu možnosť. Žiadne iné možnosti nám neostali, preto v krajine \(K_5\) okružnú cestu nenájdeme.

Predpokladajme teraz, že v niektorej krajine \(K_n\), kde \(n = 6k + 5\), možno spraviť okružnú cestu. Vyberme si navyše takú krajinu, ktorá má najmenší počet miest. Jej okružnú cestu si označme \(C\). Pozrime sa na mestá typu \(A\). Postupnosť \(k\) miest \(A_{i},\, A_{i+1},\, \dots,\, A_{i+k - 1}\) takú, že nimi za radom prechádza okružná cesta \(C\) a taktiež prechádza aj linkami \(A_{i}B_{i}\) a \(A_{i+k-1}B_{i+k-1}\) nazveme úsekom. Počet miest typu \(A\) v úseku, teda číslo \(k\), nazveme dĺžkou úseku. Dĺžka každého úseku je zjavne aspoň \(2\).

Okružná cesta \(C\) rozdelí okruh miest typu \(A\) na niekoľko úsekov. Keďže súčet dĺžok úsekov je \(n\), čo je nepárne číslo, aspoň jeden úsek musí mať nepárnu dĺžku. Nech je to úsek \(A_{i},\, A_{i+1},\, \dots,\, A_{i+k-1}\), ktorý si pomenujeme \(U\). Nech jeho dĺžka \(k\) je aspoň \(5\). Keďže linky \(A_{i+2}B_{i+2},\, A_{i+4}B_{i+4},\, \dots,\, A_{i+k-3}B_{i+k-3}\) sú nepoužité, musia byť použité linky \(B_{i}B_{i+2},\, B_{i+2}B_{i+4},\, \dots,\, B_{i+k-3}B_{i+k-1}\). Tieto linky však spolu s úsekom \(U\) vytvoria okruh.

Preto je náš úsek \(U\) dlhý \(k = 3\). Linka \(A_{i+1}B_{i+1}\) nie je použitá, preto musia byť použité linky \(B_{i-1}B_{i+1}\) a \(B_{i+1}B_{i+3}\). Z nepoužitých liniek \(B_iB_{i+2}\), \(A_{i-1}A_i\) a \(A_{i+2}A_{i+3}\) zase dostaneme použité linky \(B_iB_{i-2}\), \(B_{i+2}B_{i+4}\), \(A_{i-2}A_{i-1}\), \(A_{i-1}B_{i-1}\), \(B_{i+3}A_{i+3}\) a \(A_{i+3}A_{i+4}\). Dostaneme tak stav ako na obrázku 4.

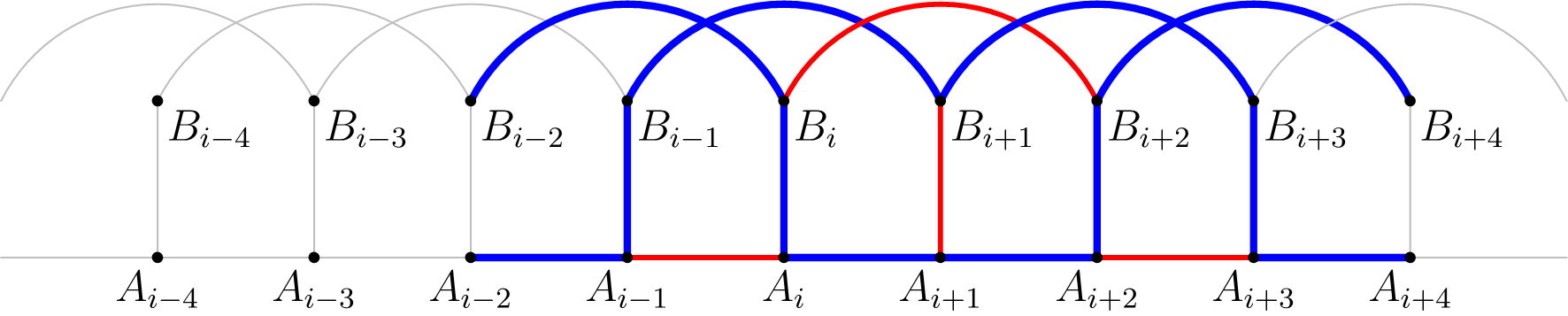
Pozrime sa, aké úseky sa nachádzajú vedľa nášho úseku \(U\). Pokiaľ je linka \(A_{i-2}B_{i-2}\) použitá, dostávame, že úsek \(U\) susedí s úsekom dĺžky \(2\). Podobne by sme úsek dĺžky \(2\) dostali, ak použijeme linku \(A_{i+4}B_{i+4}\). Ak by úsek \(U\) z oboch strán obklopovali úseky dĺžky \(2\), dostali by sme okruh cez \(2 \cdot 7 = 14 < 2n\) miest, čo nie sú všetky. Preto jedna z liniek \(A_{i-2}B_{i-2}\), \(A_{i+4}B_{i+4}\) musí byť nepoužitá. BUNV, nech je to \(A_{i-2}B_{i-2}\). V takom prípade sú použité linky \(B_{i-4}B_{i-2}\) a \(A_{i-3}A_{i-2}\) a taktiež aj \(A_{i-3}B_{i-3}\) a \(B_{i-3}B_{i-5}\). Teda sme dostali ďalší úsek dĺžky \(3\) (pozri aj obrázok 5).

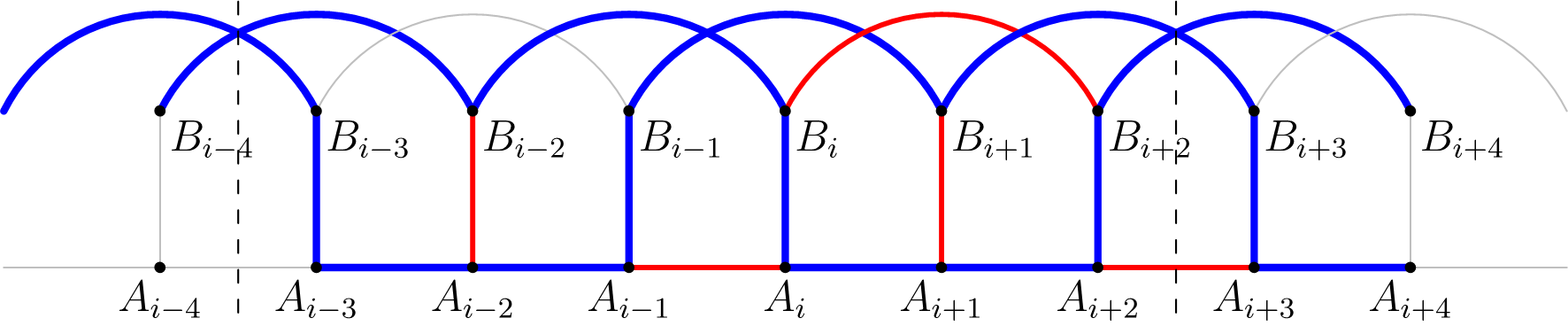
Teraz vyhodíme z krajiny \(K_n\) všetkých \(2 \cdot 6\) miest s indexmi od \(i-3\) po \(i+2\). Šesť liniek, ktoré lietali do týchto vyhodených miest zo zachovaných miest nahradíme linkami \(A_{i-4}A_{i+3}\), \(B_{i-4}B_{i+4}\) a \(B_{i-5}B_{i+3}\). Táto krajina \(K'\) má stále okružnú cestu: Prechádza z mesta \(B_{i-4}\) po pôvodnej trase po mesto \(B_{i-5}\) a potom linkou \(B_{i-5}B_{i+3}\). Ďalej pokračuje z mesta \(B_{i+3}\) do mesta \(B_{i+4}\) po pôvodnej trase a vráti sa linkou \(B_{i+4}B_{i-4}\) naspäť na začiatok. Navyše, táto krajina \(K'\) je totožná s krajinou \(K_{n-6}\), akurát má inak nazvané niektoré mestá. To je však spor, lebo krajina \(K_n\) bola vybraná ako krajina s najmenším počtom miest tvaru \(6k+5\), v ktorej možno spraviť okružnú cestu.

Týmto je náš dôkaz hotový, a teda Veronika chce ísť do krajiny \(K_n\) pre všetky celé čísla \(n \ge 3\), ktoré nie sú tvaru \(n = 6k + 5\).