8. Kolmicu Musím Spraviť vzorové riešenie

Na začiatok sa pokúsme vyťažiť niečo zo zadania. Keď si nakreslíme obrázok, asi ako prvé si poznačíme \(|\sphericalangle BAD|=|\sphericalangle CAF|\), keďže \(AD\) je os uhla \(BAC\). Tiež nám môže udrieť do očí, že \(|CD|=|CF|\), z čoho vieme \(|\sphericalangle CFD|=|\sphericalangle CDF|\), čo sa vďaka vrcholovým uhlom rovná \(|\sphericalangle ADB|\). Takýto obrázok nás navádza k tomu, že trojuholníky \(ABD\) a \(ACF\) sú podobné.

Keďže zo zadania vieme, že \(|AB|=\frac{1}{2}|AC|\), spolu s podobnými trojuholníkmi nás to istým spôsobom vedie k zadefinovaniu stredu strany \(AC\), označme ho \(S\). Keď ho dokreslíme do obrázka, os uhla \(BAC\) nás nabáda k osovej súmernosti podľa tejto osi. Práve vtedy sa bod \(B\) zobrazí na \(S\). To nás zaujíma hlavne kvôli tomu, že potom \(\sphericalangle EBF\) sa zobrazí na \(\sphericalangle ESF\), keďže body \(E\) a \(F\) sú samodružné. Teda namiesto \(|\sphericalangle EBF|=|\sphericalangle ECF|\) stačí ukázať \(|\sphericalangle ESF|=|\sphericalangle ECF|\), a teda že \(4\)-uholník \(EFCS\) je tetivový.

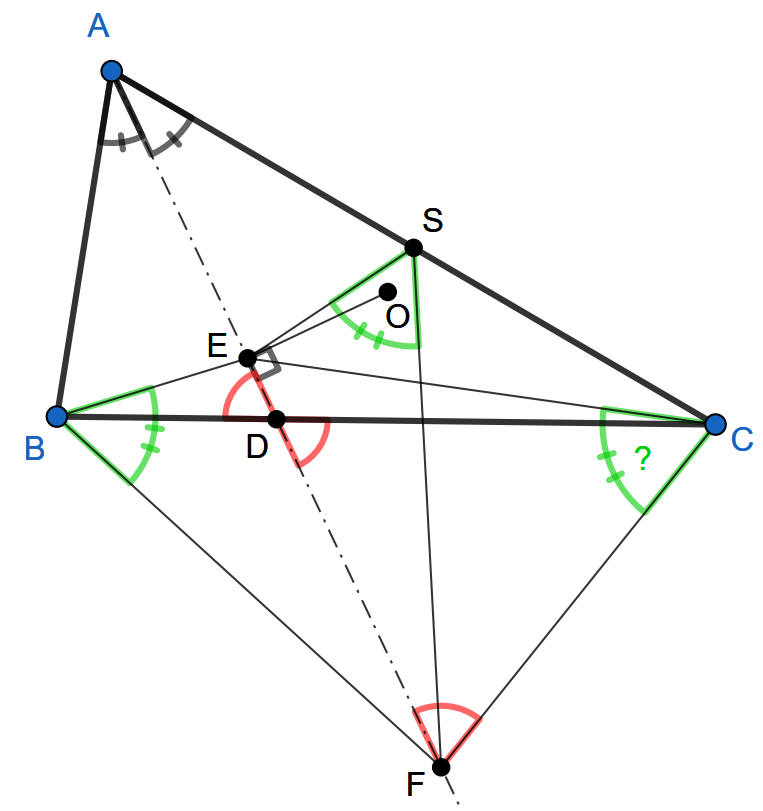
To sa zvyčajne dokazuje buď pomocou obvodových uhlov, alebo vďaka tomu, že súčet jeho protiľahlých uhlov je \(180^\circ\). Keďže už z podobných trojuholníkov \(ABD\) a \(ACF\) vieme, že platí \(|\sphericalangle ABD|=|\sphericalangle SCF|\), chceli by sme ukázať aj rovnosť \(|\sphericalangle SCF|=|\sphericalangle AES|\).

Ešte sme nevyužili, že bod \(E\) je kolmý priemet bodu \(O\) na priamku \(AD\). Taktiež bod \(O\) je špeciálny tým, že je definovaný ako priesečník osí strán trojuholníka \(ABC\). Z toho si môžme všimnúť, že \(4\)-uholník \(AEOS\) je tetivový. Preto si náš hľadaný uhol \(AES\) môžme preniesť na uhol \(AOS\). Toto je už pomerne bežný a známy uhol, keďže z vety o stredovom a obvodovom uhle platí, že \(|\sphericalangle AOC|=2\cdot|\sphericalangle ABC|\), a teda \(|\sphericalangle AOS|=|\sphericalangle ABC|\). Z toho máme \(|\sphericalangle SCF|=|\sphericalangle ABC|=|\sphericalangle AES|\) a to sme chceli.

Teraz si musíme dať pozor na konfigurácie. Bod \(S\) je vždy bližšie k bodu \(A\) ako bod \(C\), avšak to nemožno povedať o vzájomnej polohe bodov \(E\) a \(F\). Ak bod \(F\) leží na polpriamke \(EA\), vieme, že platí \(|\sphericalangle FES|=|\sphericalangle SCF|\), a teda vďaka obvodovým uhlom ležia body \(F\), \(E\), \(C\) a \(S\) na kružnici (v tomto poradí).

Ak \(F\) leží na polpriamke opačnej k polpriamke \(EA\), platí \(|\sphericalangle FES|=180^\circ-|\sphericalangle AES|=180^\circ-|\sphericalangle SCF|\). Z toho vidíme, že súčet protiľahlých uhlov v \(4\)-uholníku \(SEFC\) je \(180^\circ\), a preto je tetivový (body sú na kružnici v poradí \(E\), \(F\), \(C\), \(S\)). Ak \(E=F\), rovnosť uhlov triviálne platí (keďže ich veľkosť je \(0^\circ\)).

Iné riešenie

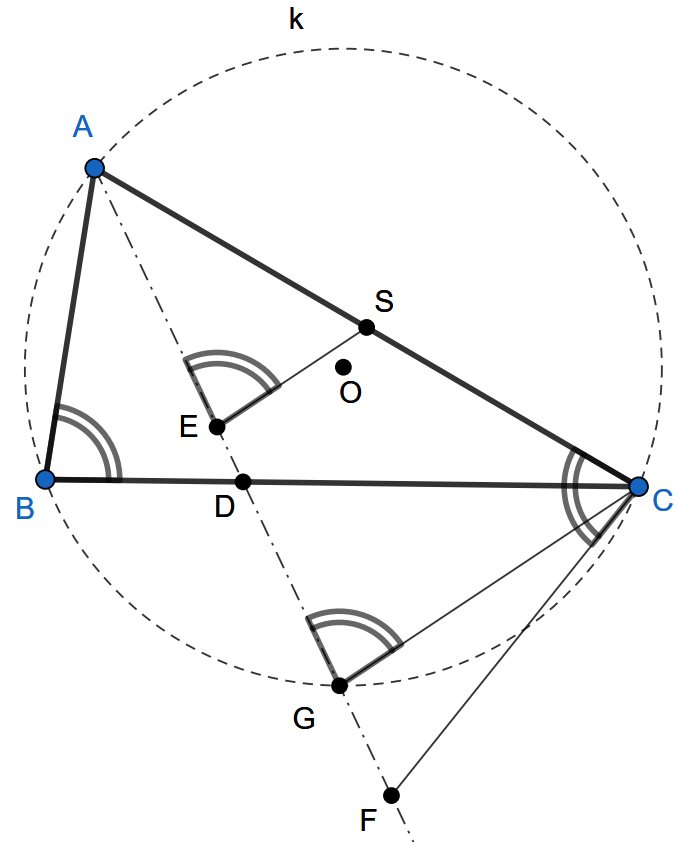
Ukážme si, ako inak možno dokázať tetivovosť \(4\)-uholníka \(EFCS\). Znova sme v bode, že chceme ukázať rovnosť uhlov \(|\sphericalangle SCF|=|\sphericalangle AES|\). Taktiež už vieme, že \(|\sphericalangle SCF|=|\sphericalangle ABC|\). Teda by sme chceli, aby platilo \(|\sphericalangle AES|=|\sphericalangle ABC|\).

Môžme si všimnúť, že bod \(A\) leží na ramene oboch uhlov. Preto si prenesme uhol \(ABC\) po kružnici opísanej trojuholníku \(ABC\) tak, aby jedno jeho rameno ležalo na priamke \(EA\). Označme si teda bod \(G\) taký, že \(G\) leží na opísanej kružnici a tiež na priamke \(EA\).

V tomto momente chceme dokázať, že \(|\sphericalangle AES|=|\sphericalangle AGC|\), kde body \(A\), \(E\), \(G\) ležia na priamke. Vďaka tomu je to ekvivalentné s tvrdením, že priamky \(ES\) a \(GC\) sú rovnobežné, resp. že úsečka \(ES\) je stredná priečka trojuholníka \(AGC\). Môžme si premyslieť, že bod \(E\) je stred tetivy \(AG\) práve preto, že je kolmým priemetom bodu \(O\) na priamku \(AD\). Preto naozaj platí \(|\sphericalangle AES|=|\sphericalangle AGC|=|\sphericalangle ABC|=|\sphericalangle SCF|\).

Samozrejme, existuje ešte mnoho ďalších riešení. Niektoré sú veľmi podobné tým vyššie uvedeným. Niektoré zas využívajú zaujímavé fakty, ako napríklad, že bod \(D\) je ťažiskom trojuholníka \(ACC'\), kde \(C'\) je obraz bodu \(C\) v osovej súmernosti podľa priamky \(AD\).