Zadanie
Knieža Mariánosz v deň rytierskeho turnaja po prvý raz v živote zočil kráľovninu nebeskú krásu zosobnenú v jej prenádhernom zlatom trojuholníku a hneď po turnaji sa rozhodol, že musí mať rovnaký. Veď musí byť najkrajší v okolí. Žiaľ, u kováča si neprečítal všeobecné obchodné podmienky a keď prišiel domov, zistil, že na čele nemá zlatý, ale bronzový trojuholník \(ABC\).
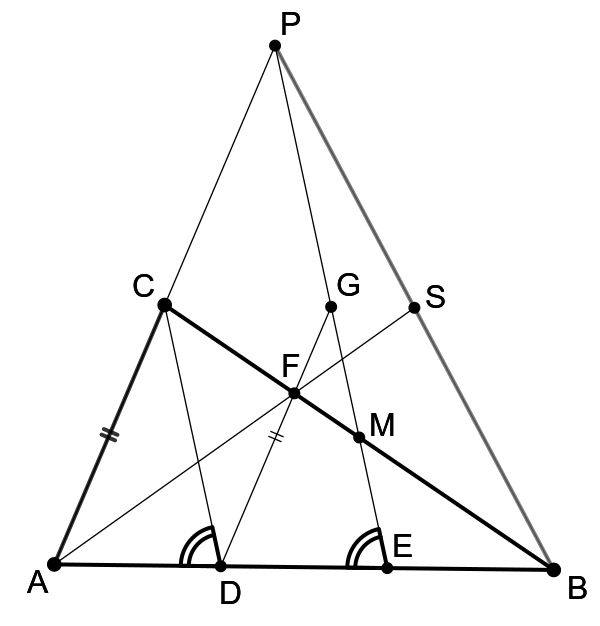
Na strane \(AB\) trojuholníka \(ABC\) sú dané body \(D\) a \(E\) tak, že platí \(|AD|=|DE|=|EB|\) a body \(A\), \(D\), \(E\), \(B\) ležia na priamke v tomto poradí. Rovnobežka so stranou \(AC\), ktorá prechádza bodom \(D\) pretína stranu \(BC\) v bode \(F\). Ďalej nech \(M\) je stred strany \(BC\). Priamka \(EM\) pretína priamku \(AC\) v bode \(P\). Dokážte, že priamka \(AF\) prechádza stredom úsečky \(BP\).
Máme dokázať, že stranu \(BP\) pretína priamka \(AF\) na polovicu. V geometrií majú túto vlastnosť ťažnice trojuholníka. Pokúsime sa teda dokázať, že úsečka \(AS\) je ťažnica. Druhá vlastnosť, ktorá nám pomôže je, že ťažnice sa pretínajú v \(\frac{2}{3}\) svojej dĺžky od vrchola. Zadefinujme si bod \(S\) ako priesečník polpriamky \(AF\) a úsečky \(BP\).
Zo zadania vieme, že \(|AD| = |DE| = |EB| = \frac{1}{3} |AB|\). Keďže robíme rovnobežku so stranou \(AC\) cez bod \(D\), dostávame dva podobné trojuholníky \(\bigtriangleup ABC\) a \(\bigtriangleup DBF\) a tiež vieme, že \(FC = \frac{1}{3} |BC|\). Teda ak by bol bod \(C\) stredom úsečky \(AP\) tak úsečka \(BC\) by bola ťažnica trojuholníka \(\bigtriangleup ABP\) a bod \(F\) by bol ťažiskom trojuholníka \(\bigtriangleup ABP\) z čoho by vyplývalo, že úsečka \(AS\) je ťažnica.
Zadefinujme si bod \(G\) ako priesečník polpriamok \(DF\) a \(EM\). Priamky \(EM\) a \(CD\) sú rovnobežné, lebo \(EM\) je strednou priečkou v trojuholníku \(CDB\). Trojuholníky \(ADC\) a \(DEG\) majú všeky dvojice strán rovnobežné, takže sú podobné. Tiež majú rovnako dlhé podstavy \(AD\) a \(DE\), takže sú zhodné. Vidíme, že \(\bigtriangleup ADC \cong \bigtriangleup DEG \thicksim \bigtriangleup AEP\). Z tohto dostaneme \[\frac{|DE|}{|AE|} = \frac{|DG|}{|AP|} = \frac{|AC|}{|AP|} = \frac{1}{2},\] z čoho vyplýva, že bod \(C\) je stredom úsečky \(AP\), a teda úsečka \(BC\) je ťažnica trojuholníka \(ABP\) a bod \(F\) je ťažiskom \(\bigtriangleup ABP\).
A keďže úsečka \(AS\) vychádza z vrcholu \(A\) a prechádza cez ťažisko \(F\), tak musí byť ťažnicou trojuholníka \(\bigtriangleup ABP\), a teda delí stranu \(BP\) na polovicu.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.