Zadanie
Vzhľadom na to, že Ákosa s vojskami stále nebolo a Matúšova armáda sa nezadržateľne blížila k Vyšehradu, rozhodla sa kráľovná Kika povolať svojich troch najspoľahlivejších pomocníkov – Kubka, Marianosza a Slava. Tí dostali za úlohu preskúmať blížiacu sa hrozbu z nového uhla a nájsť rozumné východisko z tejto šlamastiky. Žiaľ, nech sa na problém pozerali ako len chceli, výsledok bol vždy rovnaký...
V trojuholníku \(ABC\), v ktorom platí \(|AB|<|AC|\), označme \(D\) priesečník osi vnútorného uhla pri vrchole \(A\) a strany \(BC\). Nech \(P\) je priesečník osi vonkajšieho uhla pri vrchole \(A\) a kružnice opísanej trojuholníku \(ABC\) rôzny od \(A\). Uvažujme kružnicu \(k\), ktorá prechádza bodmi \(A\) a \(P\). Predpokladajme, že \(k\) pretína úsečku \(BP\) v jej vnútornom bode \(E\) a úsečku \(CP\) v jej vnútornom bode \(F\). Dokážte, že uhly \(DEP\) a \(DFP\) majú rovnakú veľkosť.
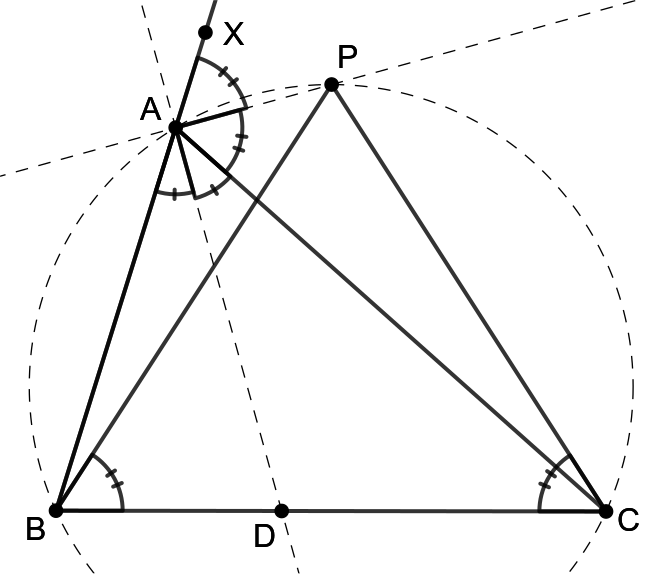
Nazačiatok sa zamyslime, čo za bod je bod \(P\). Je to priesečník osi vonkajšieho uhla a opísanej kružnice trojuholníka \(ABC\). Tento bod je význačný pre trojuholník. Nazýva sa Antišvrčkov bod a je o ňom známe, že leží presne v strede horného oblúka \(BC\) (toho oblúka, ktorý obsahuje bod \(A\)) na opísanej kružnici. Ak ste o ňom ešte nepočuli, nevadí, teraz si spomínanú vlastnosť dokážeme.
Označme si \(X\) nejaký bod na priamke \(AB\) taký, že \(A\) leží vnútri úsečky \(BX\), aby sa nám lepšie popisovali uhly. Priamka \(AP\) je os vonkajšieho uhla, čo je inak povedané, že \(|\sphericalangle PAX|=|\sphericalangle PAC|\). Nad tetivou \(PC\) máme obvodový uhol \(PAC\). Nad tetivovou \(PB\) máme obvodový uhol \(|\sphericalangle PCB|=180 ^\circ-|\sphericalangle PAB|=|\sphericalangle PAX|=|\sphericalangle PAC|\). Nad tetivami \(PB\) a \(PC\) sú rovnako veľké obvodové uhly, takže \(|PB|=|PC|\). Z toho priamo vyplývajú zaujímavé veci, napríklad že trojuholník \(PBC\) je rovnoramenný, že dĺžky oblúkov \(CP\) a \(PB\) sú rovnako veľké, a že bod \(P\) leží na ose úsečky \(BC\).
Pozrime sa teraz na úlohu z opačnej strany. Aby sme dokázali \(|\sphericalangle DEP|=|\sphericalangle DFP|\), stačí nám dokázať rovnosť ich doplnkových uhlov \(DEB\) a \(DFC\). Všimnime si, že trojuholníky \(EBD\) a \(FCD\) už majú jednu dvojicu rovnakých uhlov \(|\sphericalangle EBD|=|\sphericalangle FCD|\), keďže trojuholník \(PBC\) je rovnoramenný. Teda potrebujeme dokázať, že \(EBD\) a \(FCD\) sú podobné, aby mali rovnaké všetky uhly. Ak majú byť podobné, tak v akom pomere to bude? Predsa v pomere \(|BD|:|DC|\). To je presne pomer úsečiek, na ktoré delí priamka \(AD\) (čo je os uhla \(BAC\)) úsečku \(BC\). No a to všetci vieme, že os uhla delí protiľahlú stranu v pomere zvyšných dvoch strán trojuholníka. V našom prípade v pomere \[\frac{|BD|}{|DC|}=\frac{|AB|}{|AC|}.\] Chceli by sme ukázať, že aj strany \(BE\), \(CF\) sú v tomto pomere, aby trojuholníky \(DBE\) a \(DCF\) boli podobné.
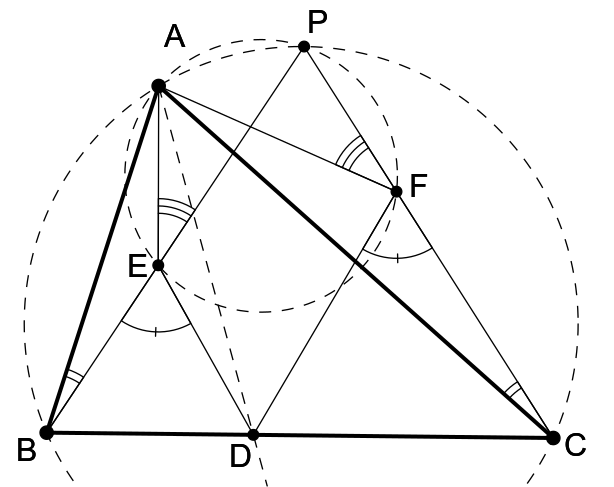
Poďme nájsť nejaké iné podobné trojuholníky, aby sme vedeli vypočítať daný pomer. Keďže \(|AB|<|AC|\), bod \(A\) leží na opísanej kružnici medzi bodmi \(B\), \(P\). Dokážeme, že trojuholníky \(ABE\) a \(ACF\) sú podobné. Platí \(|\sphericalangle ABE|=|\sphericalangle ACF|\), lebo ide o obvodové uhly nad tetivou \(AP\) na opísanej kružnici. Takisto \(|\sphericalangle AEP|=|\sphericalangle AFP|\), lebo sú obvodové na kružnici \(k\), takže sa rovnajú aj ich doplnkové uhly \(|\sphericalangle AEB|=|\sphericalangle AFC|\). Trojuholníky \(ABE\) a \(ACF\) majú rovnaké dva uhly, takže sú podobné. Zapíšme pomer podobnosti. \[\frac{|EB|}{|FC|}=\frac{|AB|}{|AC|}\]
Následne sú podobné aj trojuholníky \(EBD\) a \(FCD\), lebo \(|\sphericalangle EBD|=|\sphericalangle FCD|\) a obe dvojice strán sú v rovnakom pomere: \[\frac{|EB|}{|FC|}=\frac{|AB|}{|AC|}=\frac{|BD|}{|DC|}.\]
Preto \(|\sphericalangle DEB|=|\sphericalangle DFC|\), čo sme chceli dokázať.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.