Zadanie
V tejto úlohe, mal byť nejaký pekný historický príbeh. Žiaľ, Kika stratila svoju historickú knižku o Magalhãesovi, a tak nám neostáva nič iné, iba vám namiesto pekného čítania zadať túto šmakocinku:
Daný je ostrouhlý trojuholník \(ABC\), v ktorom platí \(|AB|<|AC|\). Označme \(O\) stred kružnice opísanej tomuto trojuholníku. Nech \(Q\) je bod taký, že \(OQ\) je priemerom kružnice \(k\) opísanej trojuholníku \(AOC\). Na priamkach \(AQ\) a \(AC\) sú dané body \(M\) a \(N\) tak, že \(AMBN\) je rovnobežník. Dokážte, že priesečník priamok \(MN\) a \(BQ\) leží na kružnici \(k\).
Uhly trojuholníka \(ABC\) budeme značiť \(\alpha,\beta,\gamma\), ako zvyčajne.
Najprv si potrebujeme uvedomiť, čo je bod \(Q\) vlastne zač. Chceme si ukázať, že je to práve bod prieniku dotyčníc ku kružnici opísanej trojuholníku \(ABC\) v bodoch \(A\) resp. \(C\). (Využijeme veľkosti uhlov \(|\sphericalangle AOC|=2 \beta\), \(|\sphericalangle OAC|=90^{\circ}-\beta\).) Platí to, pretože \(|\sphericalangle CAQ|=|\sphericalangle OAQ|-|\sphericalangle OAC|=90^{\circ}-(90^{\circ}-\beta)=\beta\), teda priamka \(AQ\) je naozaj dotyčnica (kvôli vete o úsekovom uhle). Podobne sa toto dá odvodiť aj pre priamku \(CQ\). Tým sme naše tvrdenie o bode \(Q\) ukázali. Z toho ale vyplýva, že priamka \(BQ\) je symediánou z vrcholu \(B\) v trojuholníku \(ABC\). 1.
Našou úlohou je teda ukázať, že priesečník priamky \(MN\) a \(b\)-symediány trojuholníka \(ABC\) (ktorý budeme ďalej označovať \(D\)) leží na kružnici \(AOC\).
Vieme, že priamka \(MN\) prechádza stredom úsečky \(AB\), pretože uhlopriečky rovnobežníka majú spoločný stred. Môžeme si ďalej všimnúť podobnosť trojuholníkov \(ABC\sim ANB\), pretože \(\beta=|\sphericalangle ABC|=|\sphericalangle CAQ| = |\sphericalangle ANB|\), kde tretia rovnosť nastáva kvôli \(BN \parallel AQ\). Táto podobnosť nám ďalej dáva \(|\sphericalangle DBA|=|\sphericalangle MNB|=|\sphericalangle NMA|=|\sphericalangle DMA\)|, kde druhá rovnosť vyplýva zo stredovej symetrie rovnobežníka. Prvá však potrebuje odôvodnenie: \(|\sphericalangle DBA|\) je veľkosť uhla medzi \(b\)-symediánou a stranou \(AB\), čo z definície symediány sa rovná uhlu \(b\)-ťažnice a strany \(BC\). Tento uhol sa však v podobnosti prenášajúcej trojuholník \(ABC\) na \(ANB\) práve prenesie na uhol \(MNB\), tým sme platnosť rovností ukázali.
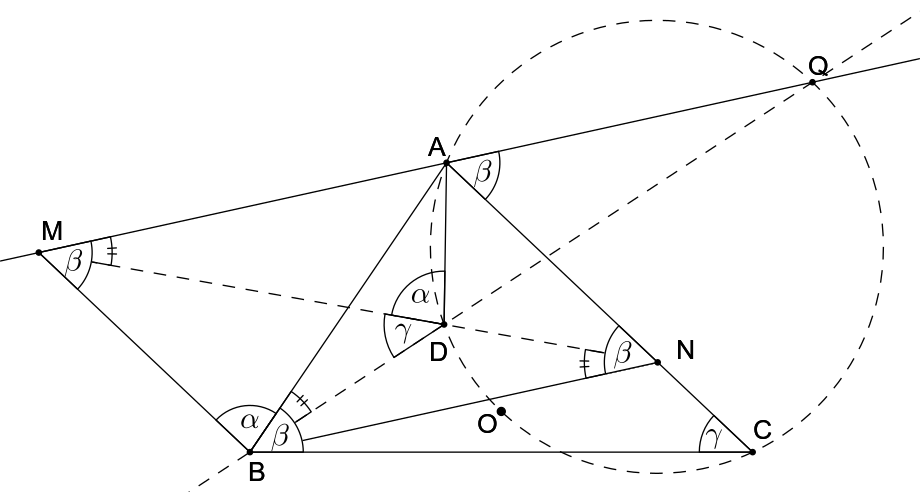
Z týchto rovností vyplýva tetivovosť štvoruholníka \(AMBD\). Ďalej vieme, že \(\beta=|\sphericalangle ANB|=|\sphericalangle BMA|\), teda kvôli tetivovsti \(|\sphericalangle ADB|=180^{\circ}-\beta\) a ďalej \(\alpha=|\sphericalangle BAN|=|\sphericalangle ABM|=|\sphericalangle ADM|\), kde druhá rovnosť platí kvôli \(AC \parallel BM\), a tretia kvôli tetivovosti. Z týchto rovností dostávame \(|\sphericalangle MDB|=|\sphericalangle ADB|-|\sphericalangle ADM|=180^{\circ}-\beta-\alpha=\gamma\), čo ale implikuje \(|\sphericalangle BDN|=180^{\circ}-\gamma\), čo nám spolu s \(|\sphericalangle BCN|=\gamma\) dáva tetivovosť \(BCND\). Z tohto a z hore uvedeného vzťahu \(|\sphericalangle ANB|=\beta\) vyplýva \(180^{\circ}-\beta=|\sphericalangle BNC|=|\sphericalangle BDC|\). Teda okolo bodu \(D\) máme tri uhly \(ADB, BDC, CDA\) spĺňajúce \(360^{\circ}=|\sphericalangle ADB|+|\sphericalangle BDC|+|\sphericalangle CDA| = 180^{\circ}-\beta+180^{\circ}-\beta +|\sphericalangle CDA|\), z čoho vyplýva \(|\sphericalangle CDA|=2\beta =|\sphericalangle COA|\), čo dokazuje tetivovosť štvoruholníka \(CADO\), čo sme chceli ukázať.
O symediánach sa môžete dozvedieť viac napríklad na 50. strane tohto dokumentu: https://prase.cz/archive/36/serial.pdf↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.