4. Klaude Monet Staropraveku vzorové riešenie

Bod \(S\) je stred kružnice opísanej \(\triangle ALO\). To znamená, že body \(A, L\) a \(O\) sú od bodu \(S\) rovnako vzdialené. Stačí nám teda zistiť ktorúkoľvek z dĺžok \(|SA|, |SL|\) alebo \(|SO|\). Keď sme si to tak zhruba \(1000\)-krát nakreslili, tak začneme mať tušenie, že aj dĺžka \(SL\) je \(l\). Tak hor sa to dokázať! Pozrime sa na štvoruholník \(LSAE\). Strany \(EL\) a \(AE\) majú dĺžku \(l\), pretože je to strana štvorca alebo strana rovnostranného trojuholníka, ktorého strana je zhodná so stranou štvorca. Bod \(E\) je teda rovnako vzdialený od bodov \(A\) a \(L\). Aj bod \(S\) je rovnako vzdialený od bodov \(A\) a \(L\). To znamená, že body \(E\) aj \(S\) ležia na osi úsečky \(AL\). Označme si priesečník úsečiek \(LA\) a \(ES\) ako \(P\).

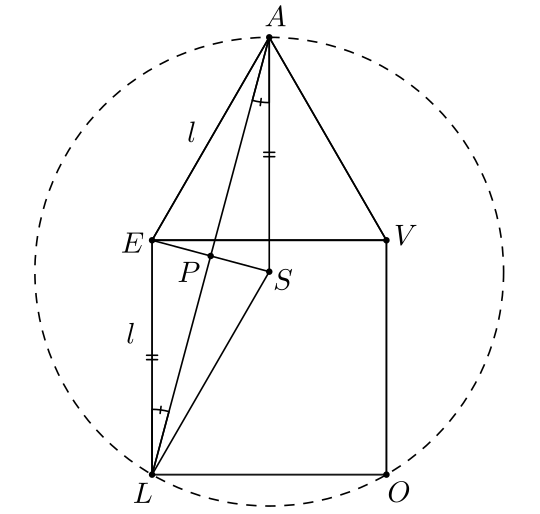
Vieme, že to je súčasne stred úsečky \(AL\), pretože priamka \(ES\) je osou úsečky \(AL\). Teda úsečky \(LP\) a \(AP\) sú rovnako dlhé. Pri bode \(P\) máme \(4\) pravé uhly, lebo \(ES\) je os úsečky. Teda uhol \(APS\) je zhodný s uhlom \(LPE\). Ak by sa nám podarilo dokázať, že aj uhol \(PAS\) je zhodný s uhlom \(PLE\), tak podľa vety \(usu\) sú trojuholníky \(APS\) a \(LPE\) zhodné, a teda dĺžka \(AS\) je zhodná s dĺžkou \(LE\), ktorá je \(l\). Bod \(S\) leží na osi úsečky \(LO\), pretože je rovnako vzdialený od bodov \(L\) a \(O\). Bod \(A\) leží na osi úsečky \(EV\), pretože trojuholník \(AVE\) je rovnostranný a teda \(|EA|=|VA|\). Úsečky \(LO\) a \(VE\) sú protiľahlé strany štvorca. To znamená že ich osi sú totožné. Teda body \(A\) a \(S\) ležia na osi \(LO\). Priamka \(AS\) je kolmá na \(LO\). Priamka \(LE\) je kolmá na \(LO\). Z toho vyplýva, že priamky \(EL\) a \(AS\) sú rovnobežné. Uhly \(PAS\) a \(PLE\) sú striedavé, čiže aj zhodné. Trojuholníky \(APS\) a \(LPE\) sú zhodné. Dĺžka úsečky \(SA\) je \(l\). To znamená, že aj dĺžka strany \(SL\) je \(l\). Pomer dĺžky \(l\) ku dĺžke strany \(|SL|\) je \(1\).

Analytické riešenie

Uložme si body do súradnicovej sústavy ako je na obrázku.

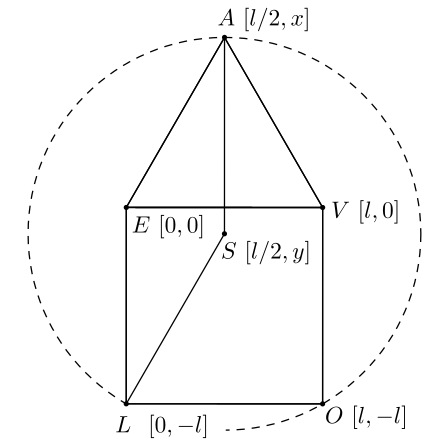
Vieme, že bod \(A\) je rovnako vzdialený od bodov \(E\) a \(V\), a preto je jeho \(x\)-ová súradnica \(l/2\). Vypočítajme \(y\)-ovú súradnicu. Spravíme to pomocou Pytagorovej vety, a síce sa pozrime na pravouhlý trojuholník, ktorý vznikne z rovnostranného trojuholníka \(AVE\), keď ho rozdelíme pomocou osi strany \(EV\). Prepona je dĺžky \(l\), jedna odvesna je \(l/2\) a druhá je \(x\). Platí \(l^2 = (l/2)^2 + x^2\). Z toho vyplýva, že \(x=(\sqrt{3}/2)l\).

Vieme, že bod \(S\) má \(x\)-ovú súradnicu \(l/2\), pretože je rovnako vzdialený od bodov \(L\) a \(O\). Bod \(S\) je rovnako vzdialený aj od bodov \(L\) a \(A\). Vzdialenosť od bodu \(L\) je \(\sqrt{(l/2-0)^2 + (y-(-l))^2}\). Vzdialenosť od bodu \(A\) je \(\sqrt{(l/2-l/2)^2 + (y-(\sqrt{3}/2)l)^2}\). Máme rovnicu \[\sqrt{(l/2-0)^2 + (y-(-l))^2} = \sqrt{(l/2-l/2)^2 + (y-(\sqrt{3}/2)l)^2},\] \[\sqrt{l^2/4 + y^2 + 2yl + l^2} = \sqrt{0^2 + y^2 - 2y(\sqrt{3}/2)l) + (3/4)l^2}.\] Z nej dopočítame \(y=-l/(2\sqrt{3}+4)\). Súradnice bodu \(S\) sú \([l/2, -l/(2\sqrt{3}+4)]\). Teraz už len vypočítame dĺžku \(SL\). Vieme, že dĺžka \(SA\) je rovnaká, a tá sa dá vypočítať asi trošku jednoduchšie. \[|SA|=\sqrt{(l/2-l/2)^2 + \left(-l/(2\sqrt{3}+4)-(\sqrt{3}/2)l \right)^2} = \dfrac{l(1+ \sqrt{3}(\sqrt{3}+2))}{2\sqrt{3}+4}.\] Po troche úprav sa nám podarí získať želaný výsledok, a síce, že \(|SL| = |SA| = l\).