Zadanie
Po tom, ako sa podarilo sušičku úspešne nastaviť, si FKSáci povedali, že takto výkonný stroj musia čo najskôr na niečom otestovať. Čo keby mala sušička príliš veľký výkon? Nemôžu si predsa zničiť svoje veci. Alebo ruky. Sušičku sa nakoniec rozhodli otestovať na najväčšom nepriateľovi FKS – rovnostrannom trojuholníku \(ABC\). FKSáci si teda zobrali svoj kľúč od KMSka a nenápadne jeden ukradli. No a čo myslite, že sa stalo, keď namierili naplno pustenú sušičku na rovnostranný trojuholník \(ABC\)? Rozletel sa na niekoľko ďalších rovnostranných trojuholníkov!
Zoberme si rovnostranný trojuholník \(ABC\). Pre ktoré celé kladné čísla \(n\) sa dá tento rovnostranný trojuholník rozdeliť na \(n\) rovnostranných (nie nutne rovnakých) trojuholníkov?
Riešenie tejto úlohy pozostáva z dvoch častí. V prvom rade potrebujeme ukázať, pre aké \(n\) môžeme rovnostranný trojuholník rozdeliť na \(n\) rovnostranných trojuholníkov. Potrebujeme ale tiež ukázať, prečo to pre iné \(n\) nejde. Mnohé z riešení obsahovali len prvú časť, preto sme ich nemohli ohodnotiť plným počtom bodov.
Vo väčšine vašich riešení sa vyskytli dva spôsoby delenia trojuholníka. Pomocou rozdelenia trojuholníka cez stredné priečky dokážeme počet trojuholníkov zvýšiť o tri. Dôležité je, že toto môžeme spraviť pre každý rovnostranný trojuholník, a teda ak ich máme \(n\), môžeme ich mať aj \(n+3\). To je dôležitý začiatok, pretože ak sa nám podarí nájsť tri za sebou idúce čísla, pre ktoré vieme trojuholník rozdeliť na toľko častí, tak to pôjde aj pre všetky vyššie.
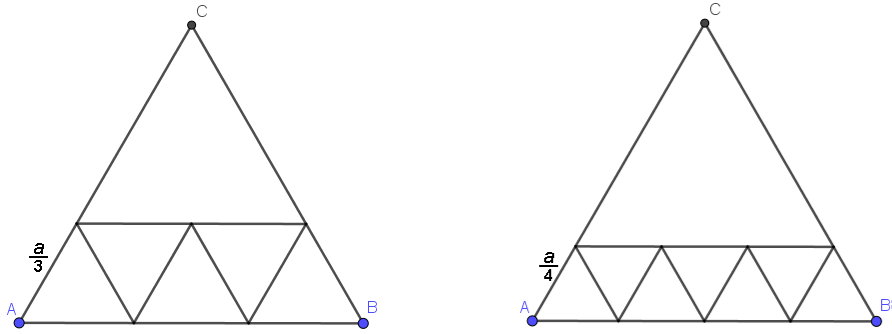
Na to, aby sme takéto tri čísla našli, ste často použili aj druhý, o niečo všeobecnejší postup. Jeho základom je rozdelenie trojuholníka na jeden trojuholník a jeden rovnoramenný lichobežník. To je možné tak, že spravíme rovnobežku s jednou so strán. Ak zvolíme vhodnú vzdialenosť od vrchola, môžeme tento lichobežník potom rozdeliť na nepárny počet trojuholníkov. Takto môžeme dostať riešenie pre \(n = 6\) a \(n = 8\). Na základe predošlého odseku dokážeme vyriešiť úlohu aj pre \(n = 7\). Z toho ale už vyplýva, že pre \(n \ge 6\) to pôjde vždy. Už predtým sme mali riešenie pre \(n = 1\) a \(n = 4\).
Ešte potrebujeme ukázať, že pre \(n = 2\), \(3\) a \(5\) úloha nemá riešenie. Tu je dobré uvedomiť si jeden základný fakt: Každý rovnostranný trojuholník má všetky uhly rovné \(60^{\circ}\). Z toho vyplýva, že vrcholy pôvodného trojuholníka musia byť aj vrcholmi niektorého z rozdelených trojuholníkov a uhol pri nich musí byť rovný \(60^{\circ}\), teda ho nemôžeme nijako deliť.
Pre \(n = 2\) by preto muselo platiť, že v niektorom z dvoch trojuholníkov sú dvoma vrcholmi vrcholy pôvodného trojuholníka. Tieto ale medzi sebou majú stranu, a keďže trojuholníky musia byť rovnostranné, išlo by o celý trojuholník \(ABC\). Teda rozdelenie na dva trojuholníky nie je možné.
Pre \(n = 3\) vychádzame z podobnej myšlienky. Ak by niektorý trojuholník obsahoval dva z troch vrcholov pôvodného, nešlo by o rozdelenie na tri trojuholníky. Preto sa každý z trojice trojuholníkov nachádza pri jednom vrchole. Pre každý trojuholník potom musia byť dve strany súčasťou dvoch strán trojuholníka \(ABC\). Tretia strana je pre každý trojuholník otočená o \(60^\circ\), pretože je rovnobežná so stranou \(ABC\), ktorá v trojuholníku nie je. To ale znamená, že žiadnu zo strán nemajú trojuholníky spoločnú, a preto musí v strede existovať nevyužitý voľný priestor. Rozdelenie na \(3\) trojuholníky teda nie je možné.
Pre \(n = 5\) opäť tri trojuholníky musia byť pri vrcholoch. Priestor, ktorý zostal môže byť buď šesťuholník, ak sa žiadne dva vrcholy malých trojuholníkov nerovnajú, päťuholník, ak sa rovná jeden, štvoruholník, ak dva a trojuholník, ak sa rovnajú všetky. My potrebujeme rozdeliť niektorý z týchto útvarov na dva rovnostranné trojuholníky.
Už sme si ukázali, že rovnostranný trojuholník na dva rovnostranné trojuholníky rozdeliť nevieme. Trojuholník, ktorý sme dostali v predošlom odseku však musí byť rovnostranný, pretože súčty dvoch strán malých trojuholníkov sa vždy musia rovnať dĺžke strany (nazvime túto dĺžku \(a\)) trojuholníka \(ABC\). Vzniká nám teda sústava rovníc \(m+n = n+o = o+m = a\), ktorej riešenie je \(n = o = m\), čo sú strany trojuholníka v strede. Ide teda o rovnostranný trojuholník a ten na dva rozdeliť nevieme.
Ak by útvarom v strede bol štvoruholník, na dva trojuholníky by sme ho mohli rozdeliť jedine uhlopriečkou, ktorú by mali spoločnú, teda by tieto dva trojuholníky museli byť zhodné.Keď spojíme pozdĺž jednej strany dva zhodné rovnostranné trojuholníky, dostaneme rovnobežník. My sme ale dostali lichobežník, ktorého jednu základňu tvoria dva spoločné vrcholy a protiľahlou základňou je časť tretej strany trojuholníka \(ABC\). Teda ani takto to rozdeliť nepôjde.
Ak by útvar v strede bol päťuholník, tak by mal súčet vnútorných uhlov \(540^\circ\). Tieto vnútorné uhly môžeme rozdeliť, no v žiadnom prípade sa súčet uhlov v rozdelenom útvare nezníži. Keďže chceme útvar rozdeliť na dva trojuholníky, potrebujeme, aby mal súčet vnútorných uhlov nanajvýš \(360^\circ\). A to päťuholník nespĺňa. Vlastne ani šesťuholník, takže úloha je vyriešená.
Rovnostranný trojuholník \(ABC\) môžeme rozdeliť na ľubovoľný prirodzený počet \(n\) rovnostranných trojuholníkov okrem \(n = 2\), \(3\) a \(5\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.