Zadanie
Medzitým Fyzikálny ústav Tomáša Suchoríka Slovenskej akadémie vied pripravil experiment s cieľom porovnať dve konkurenčné sušičky valiace sa na náš trh z Ruska. Jedna z nich je Suchoj Supersuch 100, druhá Sucharid SU-35.
Vedci z FUTS SAV získali na experiment \(303\) rôznych ľudských rúk. Každá ruka má určenú úroveň mokrosti, čo je jedno z čísel \(0\), \(1\), \(2\), a veľkosť, čo je jedno z čísel \(0,\ 1,\ \dots,\ 100\). Neexistujú dve ruky, ktoré by mali rovnakú aj mokrosť aj veľkosť. Tieto ruky následne vedci rozdelili medzi sušičky, pričom každej sušičke dali vysušiť \(151\) rúk. Platí, že súčet mokrostí rúk, ktoré má vysušiť Suchoj Supersuch 100 je rovnaký ako súčet mokrostí rúk, ktoré má vysušiť Sucharid SU-35. Rovnako aj súčet veľkostí rúk, ktoré suší Suchoj Supersuch 100 je rovnaký ako súčet veľkostí rúk, ktoré suší Sucharid SU-35. Zostane jedna ruka, ktorú nebude sušiť ani jedna sušička. Akú mokrosť a veľkosť môže mať?
Označme si ruku s veľkosťou \(i\) a mokrosťou \(j\) ako usporiadanú dvojicu \((i, j)\). Všetkých možných dvojíc (veľkosť, mokrosť) je \(101 \cdot 3 = 303\), všetkých rúk je tiež \(303\) a vieme, že žiadna dvojica sa nesmie zopakovať. To znamená, že každá dvojica (veľkosť, mokrosť) sa vyskytne ako ruka práve raz.
Vieme, že súčet mokrostí všetkých rúk okrem vynechanej musí byť párne číslo, aby sme ho vedeli rozdeliť na dve rovnaké časti, podobne aj súčet veľkostí.
Vieme ľahko vypočítať, že súčet mokrostí všetkých rúk je \((0 + 1 + 2) \cdot 101 = 303\). Pretože chceme jednu vynechať a následne zvyšok rozdeliť na dve časti s rovnako veľkým súčtom mokrostí, musí byť mokrosť vynechanej ruky nepárna, a teda \(1\).
Podobne, súčet veľkostí všetkých rúk je \(3 \cdot \frac{100 \cdot 101}{2} = 15150\). Ak chceme jednu ruku vynechať a zvyšok rozdeliť na dve časti s rovnako veľkým súčtom veľkostí, musí mať vynechaná ruka párnu veľkosť, teda vynechaná ruka má veľkosť \(2k\) pre nejaké \(k \in \{0, 1,\dots, 50\}\).
Teraz potrebujeme dokázať, že ak vynecháme ruku \((2k, 1)\), ostatné ruky vieme zakaždým vyhovujúco rozdeliť na \(2\) časti.
Všimnime si, že nám stačí pre každú vynechanú ruku \((2k, 1)\) ukázať také rozloženie, aby v prvej sušičke bol súčet mokrostí rúk \(151\) a súčet veľkostí \[\frac{15150-2k}{2} = 7575 - k.\] Ak sa nám to podarí dosiahnuť a vieme, že súčet veľkostí všetkých rúk okrem vynechanej je \(15150 - 2k\), súčet veľkostí v druhej sušičke bude tiež \(7575 - k\). Preto nám stačí vyberať ruky len do prvej sušičky, do druhej pôjdu všetky ostatné okrem tej vynechanej.
Najprv dajme do prvej sušičky ruku \((1, 1)\) a ruky \((x, 2)\) pre všetky \(26 \leq x \leq 100\).
Ešte tam pridajme ruky \((0,0)\) a \((x, 0)\) pre všetky \(2 \leq x \leq 75\).
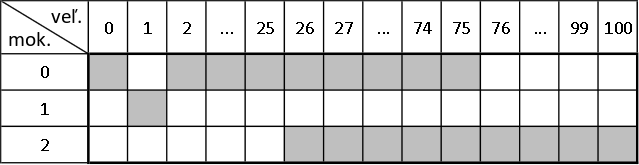
Žiadna z týchto rúk nie je tá, ktorá mala byť vynechaná, pretože je buď nepárnej veľkosti alebo párnej mokrosti. Rovnako si môžeme všimnúť, že počet rúk, ktoré sme pridelili do prvej sušičky, je presne \(151\), čo je práve toľko, koľko chceme.
Spočítajme si teraz súčet mokrostí a veľkostí rúk, ktoré sme práve pridelili prvej sušičke. Súčet mokrostí rúk v prvej sušičke je \(1 + 75 \cdot 2 + 75 \cdot 0 = 151\). Súčet veľkostí rúk v prvej sušičke je \[1 + \frac{(26 + 100) \cdot 75}{2} + \frac{75 \cdot 76}{2} - 1 = 7575.\]
My ale potrebujeme, aby súčet veľkostí rúk v prvej sušičke bol \(7575 - k\).
Ak \(k = 0\), je hotovo. Inak vymeníme ruku \((25 +k, 2)\), ktorá v prvej sušičke určite je, za ruku \((25, 2)\), ktorá tam nie je.
Tým dosiahneme potrebný súčet.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.