Zadanie
V čase vojny sa často aj nemysliteľné stáva skutočnosťou. Bolo tomu tak aj v čase grécko-perzských vojen, kedy Aténčanom pod velením Temistokla prišli na pomoc v ťažení proti Peržanom aj ich úhlavní nepriatelia – Sparťania, pod velením generála Pausania. Samozrejme, že proti sile ich spojených armád nemali Peržania šancu a utrpeli pri Platajach zdrvujúcu porážku. Po vojne je však potrebné víťazstvo nielen dobre osláviť, ale si aj rozdeliť vojnovú korisť. Keďže Peržania po sebe nič nezanechali, ostávalo si už len rozdeliť znovudobyté územie.
Temistokles aj Pausanius boli obaja praktickí muži činu. Preto sa rozhodli rozdeliť si dobyté územie v tvare trojuholníka \(ABC\) čo najkonvenčnejšie. Chceli by ho rozdeliť na dve polovice, s rovnakým obsahom tak, že ho na mape prerežú jedným rezom, ktorý bude rovnobežný so stranou \(AB\) trojuholníka \(ABC\).
K dispozícii však v tábore majú iba pravítko a kružidlo.
Pravítko dokáže zobrať dva body a narysovať priamku vedúcu cez tieto dva body.
Kružidlo dokáže spraviť kružnicu v nejakom bode s polomerom rovným vzdialenosti nejakých dvoch bodov.
Generáli teraz stoja pred ťažkým rozhodnutím rozrezať územie na dve rovnako veľké časti. Pomôžte im nájsť pomocou pravítka a kružidla takú priamku, ktorá je rovnobežná so stranou \(AB\) trojuholníka \(ABC\) a delí ho na dve časti s rovnakým obsahom. 1
Ak ste sa s podobným typom úloh ešte nestretli môže vám pomôcť krátky text na stránke: https://kms.sk/ako_riesit/konstrukcne_ulohy/↩
Spravme najprv všetky potrebné výpočty, nech vieme, čo presne chceme rysovať. Označme si postupne \(E,\, F\) body, v ktorých budú rovnobežkou prerezané úsečky \(AC,\, BC\). Z vety o súhlasných uhloch vidíme, že \(|\sphericalangle ABC|=|\sphericalangle EFC|\) a \(|\sphericalangle BAC| = |\sphericalangle FEC|\). Potom bude trojuholník \(EFC\) podobný trojuholníku \(ABC\) podľa vety \(uu\). Označme \(k\) koeficient podobnosti. Trojuholník \(ABC\) je teda v každom rozmere \(k\)-krát väčší ako \(EFC\). Keďže \(|AB| = k \cdot |EF|\) a v rovnakom pomere sú aj výšky na tieto strany, bude obsah \(ABC\) \(k^2\)-krát väčší ako obsah \(EFC\). Odtiaľ vyplýva \(k = \sqrt{2}\).
Označme pätu výšky trojuholníka \(ABC\) z vrcholu \(C\) ako \(D\). Priamka \(EF\) ju bude pretínať v jednej \(k\)-tine od bodu \(C\), teda vo vzdialenosti \(\frac{1}{\sqrt{2}} |CD| = \frac{\sqrt{2}}{2} |CD|\). Pri rysovaní budeme chcieť nájsť túto výšku a vyznačiť na nej bod v tejto vzdialenosti. Následne už len narysujeme kolmicu. Ukážme si teda priamo daný postup.
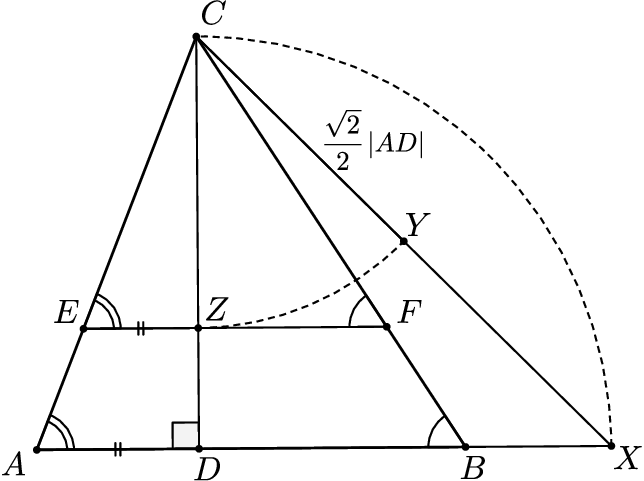
Keďže uhol \(CDA\) má byť pravý, na jeho nájdenie využijeme Tálesovu kružnicu. Nájdeme si stred úsečky \(AC\), označíme ho \(M\), a spravíme kružnicu so stredom \(M\) a polomerom \(|AM|\). Priesečník s \(AB\) bude \(D\).1
Na rozdelenie výšky využijeme vlastnosti štvorca. V ňom je uhlopriečka \(\sqrt{2}\)-krát dlhšia ako strana. Štvorec s dĺžkou strany \(CD\) tak má uhlopriečku dlhú \(\sqrt{2} \cdot |CD|\). My potrebujeme jej polovicu. Do \(D\) zapichneme kružidlo a vzdialenosť \(|CD|\) prenesieme na priamku \(AB\). Dostaneme bod \(X\), pričom \(DX\) a \(CD\) budú susedné strany štvorca. Takže \(CX\) je uhlopriečka a platí \(|CX| = \sqrt{2} \cdot |CD|\). Stred \(CX\) označíme \(Y\) a vzdialenosť \(|CY|\) prenesieme na \(CD\). Vyznačíme bod \(Z\).
Spravíme si kolmicu na \(CD\) cez bod \(Z\). Jeden zo spôsobov je spraviť si na \(CD\) taký bod \(W\), aby \(|DZ| = |ZW|\) a spraviť os úsečky \(WD\).
Kolmica, ktorú sme práve narysovali je priamo hľadaná priamka zo zadania.
Na nájdenie stredu vieme využiť postup pre os úsečky. V krajných bodoch do kružidla naberieme dĺžku úsečky a spravíme kružnice. Spojením ich priesečníkov dostaneme os úsečky, ktorá prechádza jej stredom.↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.