9. Kruhy Mysliteľa Syrakúz vzorové riešenie

Hoci úloha je zaradená až na deviatu pozíciu, jej riešenie môže byť veľmi jednoduché a intuitívne (hoci fungujú aj menej intuitívne a zložitejšie riešenia, takže ak by ste mali smolu a nenakreslili si do obrázka kľúčové čiary, stále by ste neboli stratení). Riešenie sa skladá z dvoch fáz. V prvej fáze sa pokúsime zistiť niečo viac o konfigurácii vytvorenej bodmi \(K\) a \(N\) a v druhej fáze použijeme zistené informácie na doklepnutie dotyku žiadaných kružníc.

V prvej časti, keď sa hráme s príkladom a snažíme sa čosi si všimnúť, tak budeme mať šťastie, ak si do obrázka nakreslíme osi uhlov \(BAC\) a \(BCA\). Takéto dokreslenie vyzerá fajn už predtým, ako vieme, že sa nám bude hodiť. Jednak nám osi týchto uhlov pomôžu nájsť stredy žiadaných vpísaných kružníc, dvak sa nám môže javiť zaujímavé, že na týchto osiach zároveň leží aj stred kružnice vpísanej samotnému trojuholníku \(ABC\).

Keď už tieto priamky máme nakreslené, môžeme si všimnúť (a aj to urobíme!), že nakoľko trojuholníky \(ACN\) a \(ACK\) sú rovnoramenné so základňami \(AN\) a \(CK\), tak zrovna tieto osi uhlov \(BAC\) a \(BCA\) sú v týchto trojuholníkoch aj výškami. To ale znamená, že sú výškami aj v trojuholníku \(AOC\). V tomto trojuholníku je ale výškou aj priamka \(OM\), a teda tieto tri priamky sa pretínajú v jednom bode, ktorým je stred vpísanej kružnice v trojuholníku \(ABC\). To ale znamená, že \(M\) je bodom dotyku kružnice vpísanej trojuholníku \(ABC\) a strany \(AC\). Týmto zistením je prvá fáza úspešne ukončená.

V druhej fáze sa vieme zbaviť značnej časti príkladu. Stačí nám už totiž iba dokázať, že majúc základný trojuholník \(ABC\) a bod \(M\) predefinovaný ako dotyk trojuholníka s jemu vpísanou kružnicou, tak kružnice vpísané \(AMB\) a \(CMB\) sa dotýkajú. Táto fáza je založená na známom a jednoduchom tvrdení o dĺžkach úsekov medzi bodom dotyku vpísanej kružnice a vrcholom trojuholníka. Spomínané tvrdenie vyjadruje dĺžky týchto úsekov pomocou dĺžok strán trojuholníka (a okrem samotného vyjadrenia z neho aj vyplýva, že dĺžky úsekov z jedného vrchola sa rovnajú). ¹

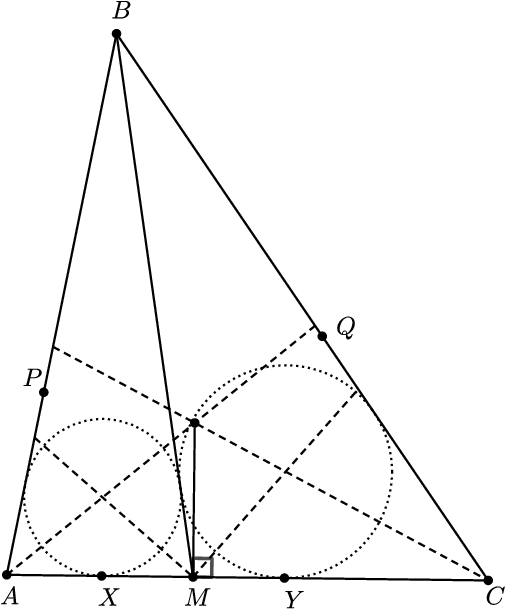
Všimnime si najskôr, že na to, aby sa nám kružnice dotýkali, musí byť vzdialenosť od bodu \(M\) do bodov dotyku týchto kružníc so spoločnou stranou \(MB\) rovnaká. Tieto vzdialenosti si vieme vďaka známej vlastnosti preniesť na stranu \(AC\). Označme si preto \(X\) a \(Y\) postupne bod dotyku kružnice vpísanej trojuholníku \(AMB\) so stranou \(AC\) a bod dotyku kružnice vpísanej trojuholníku \(CMB\) so stranou \(AC\). Chceme ukázať rovnosť \(|XM|=|MY|\).

Na dôkaz tejto rovnosti využijeme spomínaný vzorec, pomocou ktorého môžeme oboje dĺžky vyjadriť pomocou dĺžok strán v trojuholníkoch \(AMB\) a \(CMB\). Tento vzorec aplikovaný na stranu \(XM\) má nasledovný tvar: \(|XM|=\frac{1}{2}(|MA|+|MB|-|AB|)\) a podobne \(|YM|=\frac{1}{2}(|MC|+|MB|-|CB|)\). Ak dáme tieto dve vyjadrenia do rovnosti, tak po jednoduchých úpravách nám zostane overiť platnosť: \(|AB|-|MA|=|CB|-|MC|\) (tu došlo ešte aj k výmene znamienok na oboch stranách rovnice). Táto rovnosť ide ukázať buď opätovným využitím rovnakého vzorca, tentoraz aplikovaného na trojuholník \(ABC\) a jeho vpísanú kružnicu, alebo aj nasledovne. Označme ešte \(P\) a \(Q\) body dotyku vpísanej kružnice trojuholníku \(ABC\) so stranami \(AB\) a \(CB\). Potom vieme, že \(|MA|=|AP|\) a \(|MC|=|CQ|\), čím vieme našu rovnosť upraviť na \(|AB|-|AP|=|CB|-|CQ|\). To je ale ekvivalentné \(|BP|=|BQ|\), čo samozrejme platí, nakoľko \(B\) môžeme vnímať ako priesečník dotyčníc ku kružnici vpísanej \(ABC\). (Navyše rovnakú rovnosť sme už v úlohe využili niekoľkokrát. Ak ste si to neuvedomili, prečítajte si tento odstavec ešte raz.)