Zadanie
Dante pokrýval so svojou firmou okrajovú časť ekonomického záujmu. Mal za úlohu riešiť problémy, ktoré sa občas v meste vyskytli. Matematické problémy. Aj napriek nepočetnej cieľovej skupine sa mu darilo, pretože jeho zákazníci boli zámožní a dobre mu platili. Napríklad taký admirál Ulysses S. bol celkom grand. To znamená, že dobre platil. Nerád však za muníciu, preto si zavolal Danteho agentúru, aby mu vyriešila tento problém:
Na mori – pozri obrázok – sa nachádza na neznámom mieste loď tvaru T-čka – ako na obrázku – pričom však môže byť ľubovoľne otočená. „Na koľko najmenej políčok potrebujem vystreliť,“ pýtal sa admirál Ulysses S., „aby som s istotou trafil loď v mori bez ohľadu na to, kde sa nachádza? A poriadne mi aj zdôvodnite, že na menej výstrelov mi to nie vždy vyjde, nebudem tu predsa plytvať muníciou!“
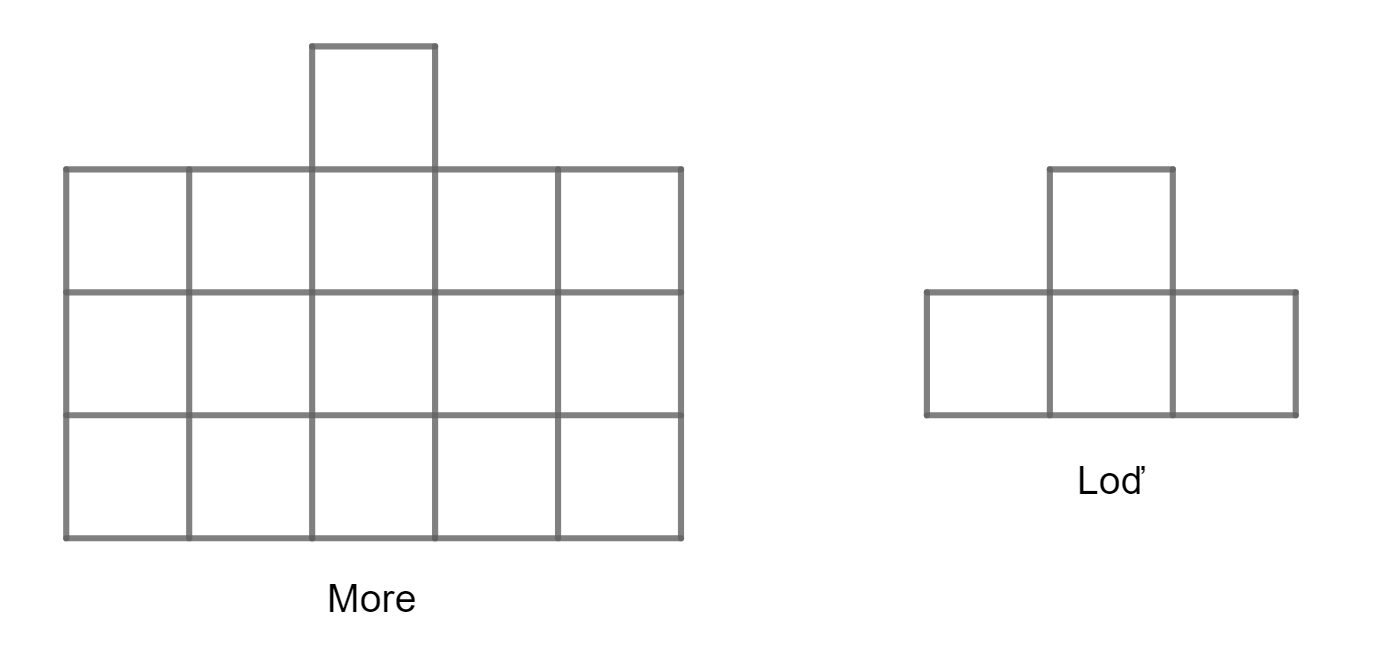
Máme zistiť na koľko najmenej políčok musíme vystreliť, aby sme loď zasiahli bez ohľadu na jej polohu. Poďme sa pozrieť na to, aké unikátne pozície môže loď zaberať, teda také, ktoré sa neprekrývajú. Keďže naša plocha má \(16\) políčok a loď zaberá \(4\), teda takýchto pozícií môže byť najviac \(4\).
Začnime v ľavom dolnom rohu. Na to aby sa časť loď nachádzala v rohu musí byť plochá strana lode popri kraji mora. Máme na výber buď horizontálne alebo vertikálne. Ale vertikálne nám nevyhovuje, lebo si odrežeme dve políčka, použijeme horizontálnu (červená loď na obrázku). Ak zrkadlovo zoberieme takúto pozíciu na druhej strane, jednoznačne dostaneme aj tretiu aj štvrtú, ktoré sa nachádzajú medzi nimi. Dostaneme takéto rozdelenie:
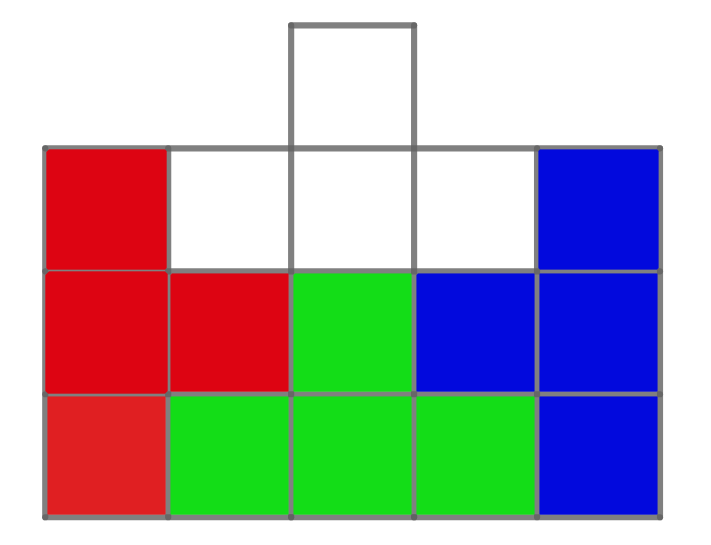
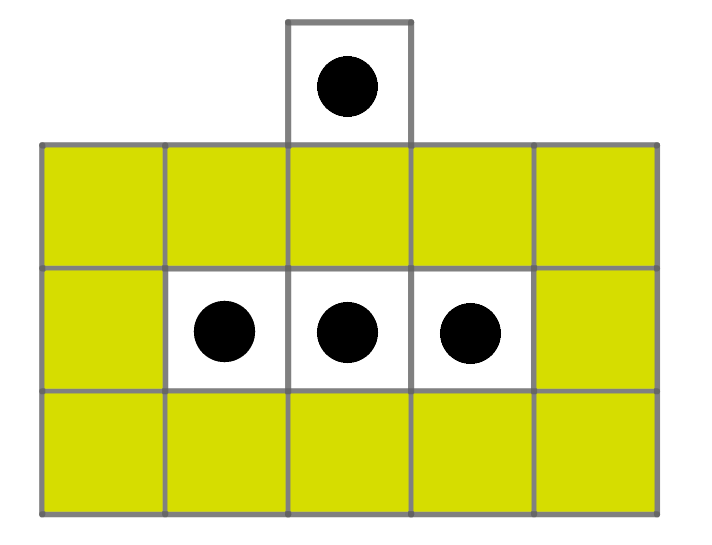
Pri tomto rozdelení vieme, že do každej farby musí padnúť minimálne jedna strela, ak chceme mať istotu, že trafíme loď. Teda potrebujeme minimálne štyri výstrely. Ale tá strela nemôže padnúť hocikam, ak chceme trafiť na istotu ľubovoľnú loď. Každá loď je presne daná svojim špicom. Ak vystrelíme do špicu každej našej zóny, tak ostanú nezasiahnuté len pozície, kam sa nezmestí celá loď (prinajlepšom len loď bez špicu), teda loď určite zasiahneme.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.