1. Koniec Matfyzného Štúdia vzorové riešenie

Všetky strany šesťuholníka majú rovnakú dĺžku \(a\). Rozdeľme si šesťuholník na \(6\) zhodných rovnostranných trojuholníkov, ktoré majú spoločný vrchol \(O\) v strede šesťuholníka, tak ako na obrázku vľavo. (Rozmyslite si ako dokázať, že tieto trojuholníky sú rovnostranné, len pomocou definície, že šesťuholník má rovnaké strany aj uhly. Tu to budeme považovať za známy a ľahko nahliadnuteľný fakt.) Trojuholník \(GED\) má uhly \(GED\) aj \(GDE\) veľkosti \(180^\circ-120^\circ=60^\circ\), takže je tiež rovnostranný, so stranou dĺžky \(|ED|=a\).

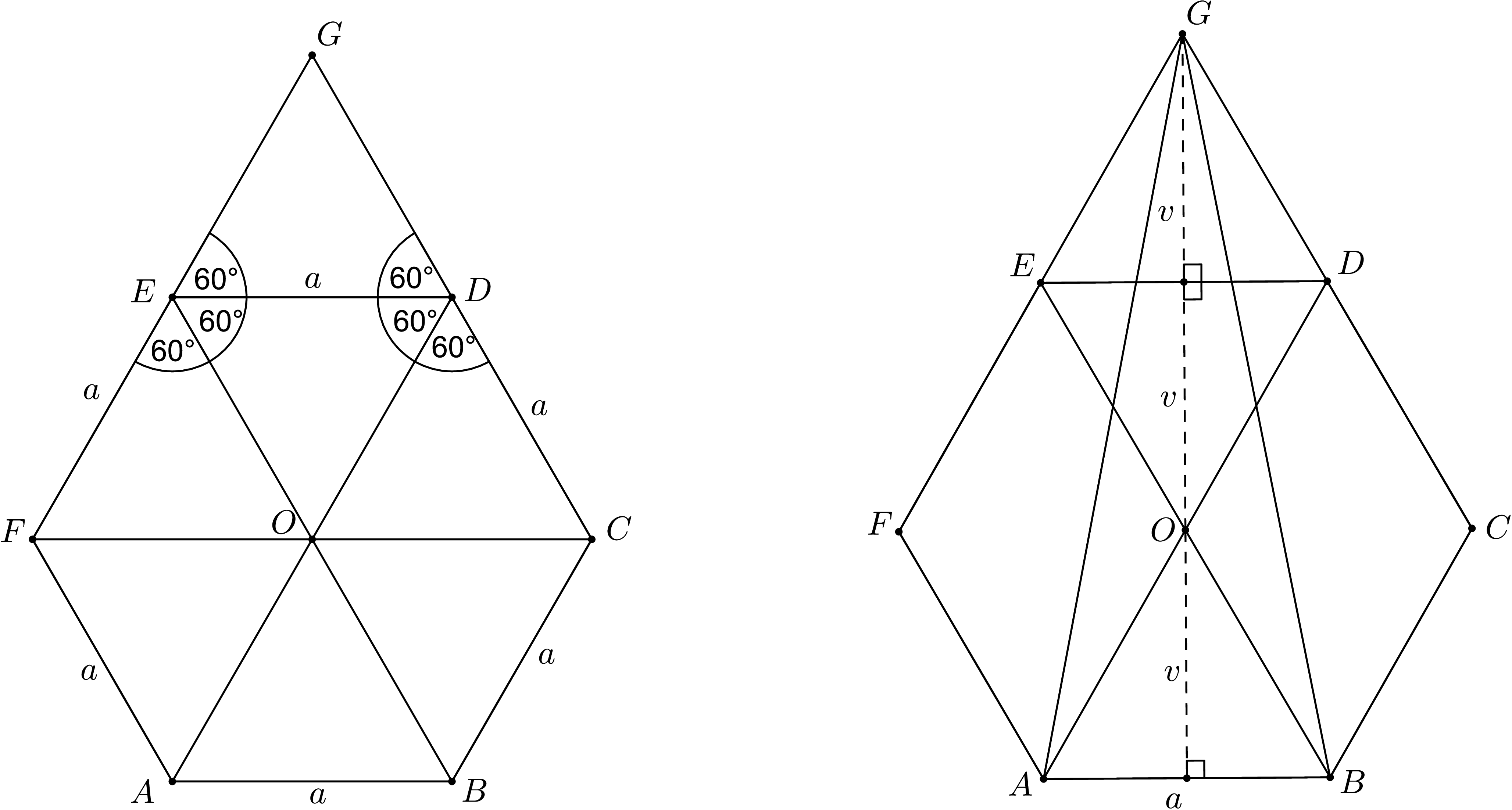
Na obrázku vpravo máme tri rovnostranné trojuholníky \(ABO\), \(EDO\) a \(EDG\), ktoré majú rovnobežné základne \(AB\) a \(ED\). Výšky týchto trojuholníkov budú ležať na jednej priamke, konkrétne na priamke \(OG\). Platí to, lebo výšky v trojuholníkoch \(EDO\) a \(EDG\) majú spoločný bod v strede strany \(ED\), keďže ide o rovnostranné trojuholníky a všetky tri výšky sú rovnobežné, lebo sú kolmé na rovnobežné základne. Všetky tri výšky majú rovnakú dĺžku \(v\), keďže ide o zhodné trojuholníky.

Vidíme, že trojuholník \(ABG\) má základňu \(a\) a výšku \(3v\). Obsah trojuholníka \(ABO\) je šestina obsahu celého šesťuholníka, \(S=\frac{1}{6}\) a zároveň \(S=\frac{1}{2}av\). Teraz by sme mohli vypočítať pomocou Pytagorovej vety, že v rovnostrannom trojuholníku platí \[v=\frac{\sqrt{3}}{2}a,\qquad S=\frac{\sqrt{3}}{4}a^2,\] a dorátať presnú dĺžku \(a\) a \(v\), ale my to spravíme šikovnejšie.

Keďže trojuholník \(ABG\) má rovnakú základňu a \(3\)-krát väčšiu výšku ako \(ABO\), tak musí mať \(3\)-krát väčší obsah. \[S_{ABG}=\frac{a(3v)}{2}=3\frac{av}{2}=3S=3\cdot \frac{1}{6}=\frac{1}{2}\]

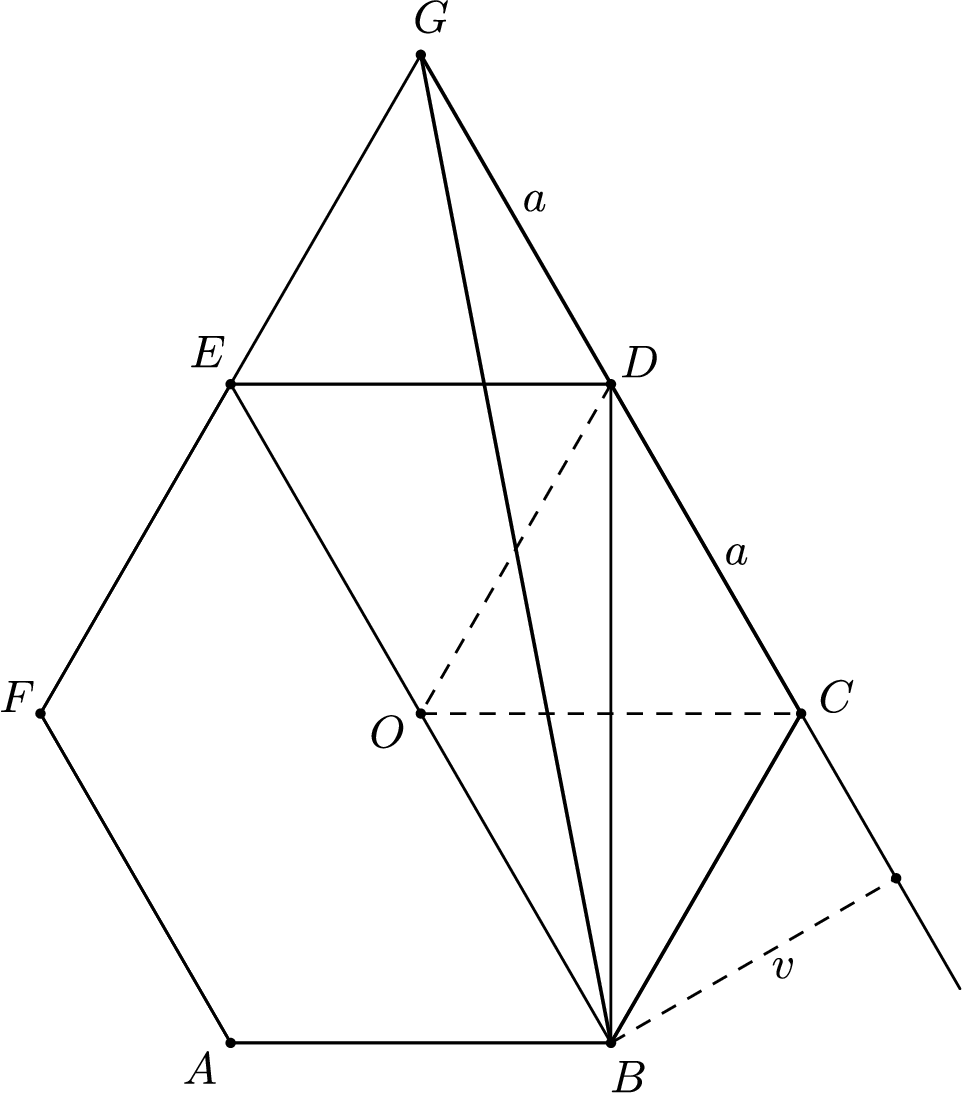
Ostáva nám trojuholník \(GCB\), ktorý má základňu \(|GC|=|GD|+|DC|=2a\). Potrebujeme ešte výšku na túto základňu. Stačí si uvedomiť, že úsečka \(OB\) je rovnobežná s \(GC\), lebo \(|\sphericalangle OBC|+|\sphericalangle BCD|=60^\circ+120^\circ=180^\circ\), takže sú rovnobežné. Preto vzdialenosť bodu \(B\) od priamky \(GC\) je rovnaká ako vzdialenosť bodu \(O\) od priamky \(GC\). Táto vzdialenosť je výška v trojuholníku \(CDO\), čo je \(v\). Výška trojuholníka \(BCG\) je teda tiež \(v\). Trojuholník \(GCB\) má \(2\)-krát väčšiu základňu a rovnakú výšku ako trojuholník \(CDO\), takže má \(2\)-krát väčší obsah, konkrétne \(2 \cdot \frac{1}{6}=\frac{1}{3}.\)

Poznámka. Chceli by sme ešte objasniť bodovanie, pretože pomerne veľa riešiteľom sme museli strhnúť body za nedostatočné zdôvodnenie faktov a pozorovaní, ktoré sa využívali v tejto úlohe. Vyžadovali sme poriadny matematický dôkaz vašich tvrdení, pretože len na základe pozorovania z obrázku si nemôžeme byť na \(100\%\) istý, že to tak skutočne je. Bodovanie teda bolo: 1b – pozorovanie, že trojuholník \(EDG\) je rovnostranný s dĺžkou strany \(a\), 1b – dôkaz tohto tvrdenia, 1b – výška trojuholníka \(ABG\) je \(3v\), 2b – dôkaz, 1b – správna hodnota obsahu \(ABG\), ďalej ste viacerí postupovali tak, že \(BCG\) a \(AFG\) sú zhodné trojuholníky, takže 1b – uvedomenie si zhodnosti trojuholníkov \(BCG\) a \(AFG\), 1b – dôkaz, že sú zhodné, 1b – hodnota obsahu \(BCG\).