Zadanie
V druhý deň svojho pobytu sa Kubko vybral do Osaky navštíviť ten povestný hrad, ktorý zohrával dôležitú rolu pri zjednotení Japonska v šestnástom storočí. Hneď na prvý pohľad ho upútali prekrásne sakurové záhrady črtajúce sa pod hradbami mohutného hradu, ako aj rovnostranné vlajky klanu Tojotomi. Práve tieto vlajky nás inšpirovali k ďalšej úlohe. Veríme, že sa vám bude páčiť.
Je daný rovnostranný trojuholník \(ABC\). Na strane \(AB\) leží bod \(D\), rôzny od bodov \(A,B\). Na polpriamke opačnej k polpriamke \(AC\) leží bod \(E\) tak, že \(|BD| = |AE|\). Dokážte, že \(|DE| = |DC|\).
Ako prvé je dobré uvedomiť si, čo znamená tvrdenie, ktoré máme dokázať. Rovnosť \(|DE|=|DC|\) znamená, že bod \(D\) je rovnako vzdialený od bodov \(E\), \(C\). Množina takýchto bodov je práve os úsečky \(EC\). Je to známy fakt, ale idea jeho dôkazu nám ďalej pomôže v riešení: Ak päta kolmice z bodu \(D\) na priamku \(EC\) je bod \(F\), tak z Pytagorových viet pre trojuholníky \(CFD\) a \(EFD\) dostávame \(|CF|^2+|FD|^2=|CD|^2=|ED|^2=|EF|^2+|FD|^2\Leftrightarrow |CF|^2=|EF|^2\). Teda daný bod \(D\) je rovnako vzdialený od bodov \(E\), \(C\) práve vtedy, keď leží na kolmici na priamku \(EC\) prechádzajúcej stredom úsečky \(EC\).
Teda našou úlohou je ukázať, že \(D\) leží na osi úsečky \(EC\). Ako sme uviedli pred chvíľou, pre dôkaz tohto nám stačí ukázať, že \(|EF|=|CF|\), kde \(F\) je päta kolmice z \(D\) na \(EC\). Tak poďme si toto ukázať.
Nech dĺžka strany rovnostranného trojuholníka je \(a\) a \(|BD|=d\). Potom si môžeme ľahko vypočítať \(|EC|=a+d\), \(|AD|=a-d\). Teraz to, čo potrebujeme ukázať, je vlastne \(|CF|=(a+d)/2\).
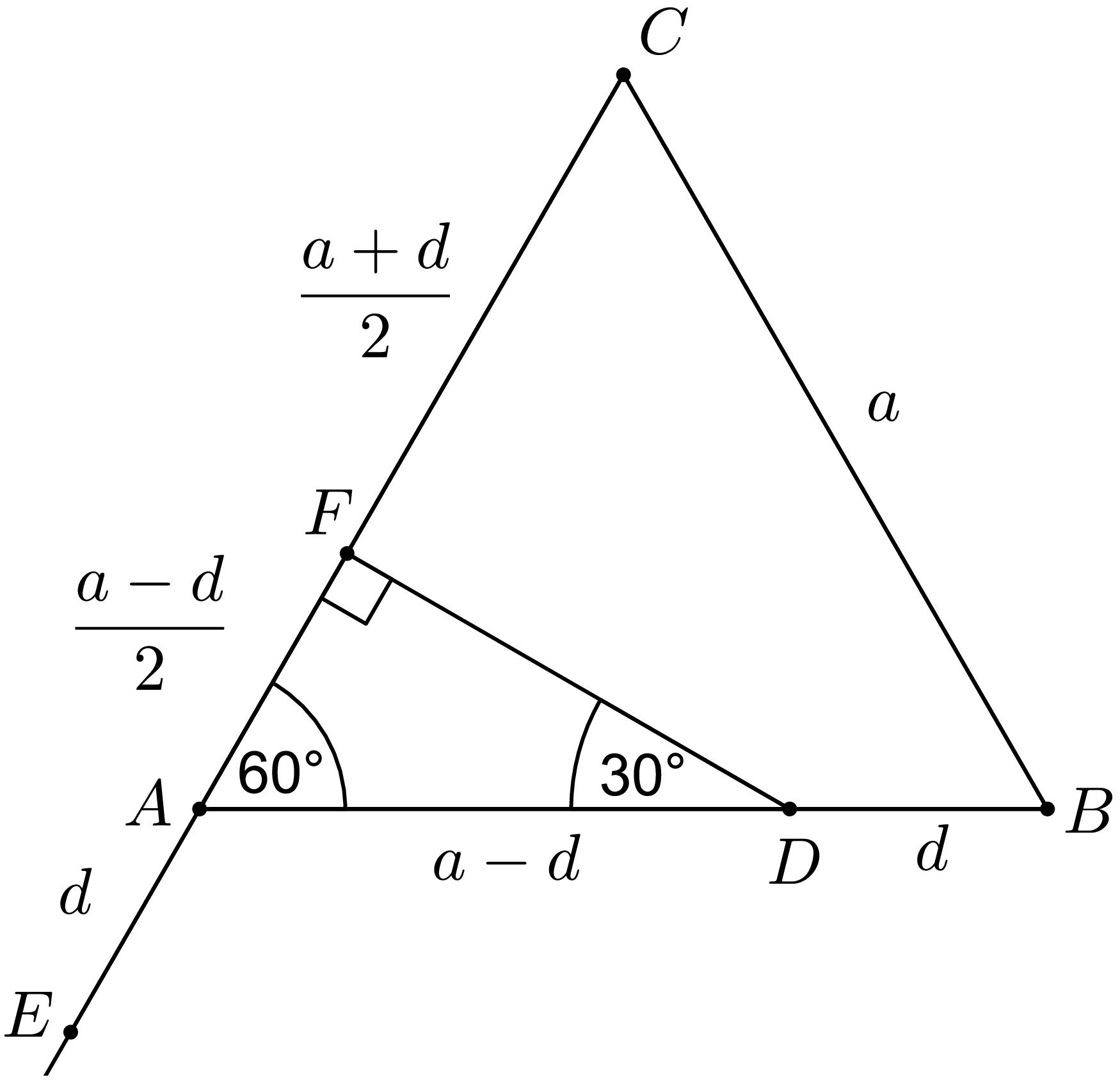
Poďme sa teraz pozrieť na trojuholník \(AFD\). Je to pravouhlý trojuholník s pravým uhlom pri vrchole \(F\) a uhlom veľkosti \(60^{\circ}\) pri vrchole \(A\). Má teda uhly \(30^{\circ}\), \(60^{\circ}\), \(90^{\circ}\), a to znamená, že dĺžka prepony \(AD\) a odvesny \(AF\) sú v pomere \(2:1\). Krátky dôkaz tohto tvrdenia je, že ak premietneme trojuholník \(AFD\) cez priamku \(DF\), tak dostaneme rovnostranný trojuholník \(DAA_1\), teda \(2|AF|=|AA_1|=|AD|\) alebo pre pokročilejších riešiteľov vychádza to z faktu \(\sin(30^{\circ})=\frac 12\). Teda kvôli rovnosti \(|AD|=a-d\) platí \(|AF|=(a-d)/2\). Teda nám vychádza \[|AC|=|AF|+|FC|\Leftrightarrow |CF|=a-\frac{a-d}{2}=\frac{a+d}{2}.\] A práve toto sme si chceli ukázať, pretože, ako sme ukázali vyššie, je to ekvivalentné so zadaním úlohy. Tým sme dôkaz dokončili.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.