Zadanie
Bolo štvrtého januára, keď sme dorazili ku Bránam Abstrakcie. Teda, buď bolo štvrtého januára, alebo štyritisíceho dodekatóbra, keďže náš kalendár podľahol Abstrakcii ako prvý, a okrem toho sa ani nedalo hovoriť o Bránach – skôr o Nenápadných Dvierkach V Stene Za Ohybom Rieky, Ledva Vysokých Pre Urasteného Školáka. Ani sme sa nenamáhali rozložiť stany, keďže sme vedeli, čo sa s niečím tak zložitým stane po vystavení Abstrakcii, a rovno sme sa pokúsili Dvere otvoriť. Na to potreboval Matrodej Lambzduch uplatniť svoj Konkretizátor, žiaľ, prístroj mu pred očami začal obrastať dokonalými geometrickými útvarmi a Lambzduch musel narýchlo zisťovať, kde končí Konkretizátor a kde začína akési euklidovské čudo.
V lichobežníku \(ABCD\), kde \(AB \parallel CD\), platí \(|AB| = 2\cdot|CD|\). Označme \(K, L\) postupne stredy strán \(BC, CD\). Vypočítajte obsah trojuholníka \(AKL\), ak obsah \(ABCD\) je \(12\).
Obsah lichobežníka vieme vypočítať ako \[\frac{(|AB|+|CD|) \cdot v}{2},\] kde \(v\) je jeho výška. Zo zadania vieme, že \(|AB| = 2|CD|\), a že obsah \(ABCD\) je \(12\). Preto musí platiť: \[\frac{(3|CD|) \cdot v}{2} = 12,\] teda \(\mathbf{|CD| \cdot v = 8}\).
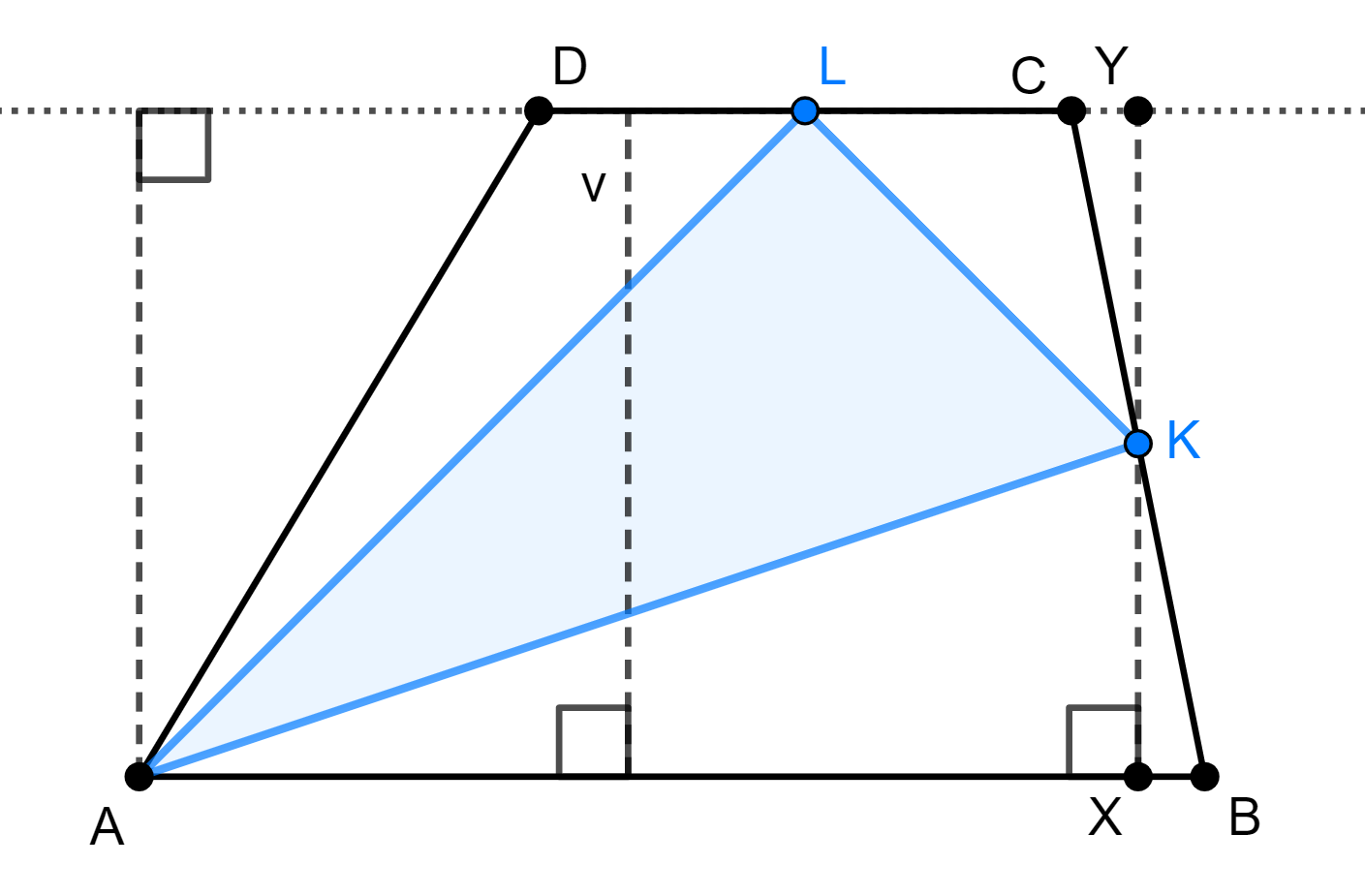
O obsahu samotného trojuholníka \(AKL\) toho zatiaľ nevieme veľa povedať, ale môžeme sa skúsiť pozrieť na trojuholníky \(LDA\), \(ABK\) a \(KCL\).
Obsah trojuholníka \(LDA\) je \(\frac{|LD|\cdot v}{2}\), keďže výška tohto trojuholníka na stranu \(LD\) je tiež výškou lichobežníka \(ABCD\), a teda jej dĺžka je \(v\). Keďže bod \(L\) leží v strede strany \(CD\), tak platí, že \(|LD| = \frac{|CD|}{2}\), preto obsah trojuholníka \(LDA\) je \[\frac{\frac{|CD|}{2} \cdot v}{2}.\] Keďže už vieme, že \(|CD|\cdot v = 8\), tak potom \[\frac{\frac{|CD|}{2} \cdot v}{2} = \frac{8}{4}=2,\] teda obsah trojuholníka \(\mathbf{LDA}\) je \(\mathbf{2}\).
Keď si zoberieme pomocnú úsečku \(XY\), ktorá tvorí výšku lichobežníka \(ABCD\) a prechádza bodom \(K\), tak zároveň úsečka \(XK\) tvorí výšku trojuholníka \(ABK\) na stranu \(AB\) a úsečka \(YK\) tvorí výšku trojuholníka \(KCL\) na stranu \(CL\). Ukážeme si, že obe tieto úsečky majú dĺžku \(\frac{v}{2}\).
Keďže \(XY\) je výškou lichobežníka \(ABCD\), tak \(|XY| = v\). Platí aj, že \(|\sphericalangle BXK| = |\sphericalangle CYK|\) (pravé uhly), \(|\sphericalangle BKX| = |\sphericalangle CKY|\) (vrcholové uhly), a teda aj \(|\sphericalangle XBK| = |\sphericalangle YCK|\). Okrem tohto ešte vieme, že bod \(K\) leží v strede strany \(BC\), teda \(|BK| = |CK|\). Preto sú trojuholníky \(BXK\) a \(CYK\) zhodné, a teda \(|XK| = |YK| = \frac{v}{2}\). S týmito informáciami už jednoducho dopočítame aj obsahy trojuholníkov \(ABK\) a \(KCL\).
Obsah trojuholníka \(\mathbf{ABK}\) môžeme vypočítať ako \[\frac{|AB|\cdot |XK|}{2} = \frac{2|CD|\cdot \frac{v}{2}}{2} = \frac{|CD| \cdot v}{2} \mathbf{= 4},\] keďže \(|CD|\cdot v = 8\).
Vieme, že bod \(L\) leží v strede strany \(CD\), teda \(|CL| = \frac{|CD|}{2}\), preto obsah trojuholníka \(\mathbf{KCL}\) zas môžeme vypočítať ako \[\frac{|CL|\cdot |YK|}{2} = \frac{\frac{|CD|}{2} \cdot \frac{v}{2}}{2} = \frac{|CD| \cdot v}{8} \mathbf{= 1},\] keďže \(|CD|\cdot v = 8\).
Keď už poznáme obsahy trojuholníkov \(LDA\), \(ABK\) a \(KCL\), tak obsah trojuholníka \(AKL\) ľahko dopočítame, ak od obsahu celého lichobežníka odpočítame obsahy týchto troch trojuholníkov, teda obsah trojuholníka \(\mathbf{AKL}\) je \(\mathbf{12-2-4-1 = 5}\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.