3. KaPor Medzipolia Spája vzorové riešenie

Na narysovanie rovnostranného trojuholníka by sme ideálne chceli poznať dĺžku jeho strany. My však máme informáciu o jeho obsahu. Na začiatok sa teda pokúsime vyjadriť podmienku zo zadania pomocou strany trojuholníka.

Majme teda rovnostranný trojuholník so stranou \(a\). Jeho obsah bude \(\frac{1}{2} a \cdot v\), kde \(v\) je výška tohto trojuholníka. Keďže je však rovnostranný, jeho výška je zároveň ťažnicou. Dostávame teda pravouhlý trojuholník s odvesnami \(\frac{1}{2}a,\, v\) a preponou \(a\). Potom podľa Pytagorovej vety \[v^2 = a^2 - \frac{1}{4}a^2 = \frac{3}{4}a^2,\] \[v = \frac{\sqrt{3}}{2}a.\] Obsah teraz už ľahko vyjadríme ako \[S = \frac{\sqrt{3}}{4}a^2.\]

Teraz prepíšeme podmienku zo zadania pomocou strán. Strany trojuholníkov s obsahom \(S_1\) a \(S_2\) budú postupne \(a_1\) a \(a_2\), stranu trojuholníka, ktorý chceme skonštruovať označíme \(a_3\). Podmienka teda hovorí \[\frac{\sqrt{3}}{4}a_1^2 + \frac{\sqrt{3}}{4}a_2^2 = \frac{\sqrt{3}}{4}a_3^2,\] \[a_1^2 + a_2^2 = a_3^2.\] Pri úprave sme celú rovnicu vydelili číslom \(\frac{\sqrt{3}}{4}\). Strany trojuholníkov teda spĺňajú podmienku Pytagorovej vety. Na narysovanie strany \(a_3\) nám stačí skonštruovať pravouhlý trojuholník s odvesnami \(a_1,\, a_2\). Pustime sa do toho.

Na začiatok si pripomeňme veci, ktoré vieme robiť, a ktoré sa nám zídu. Samozrejme vieme rysovať kružnice, priamkou spojiť dva body, ale aj prenášať dĺžky úsečiek a rysovať kolmice cez nejaký bod.

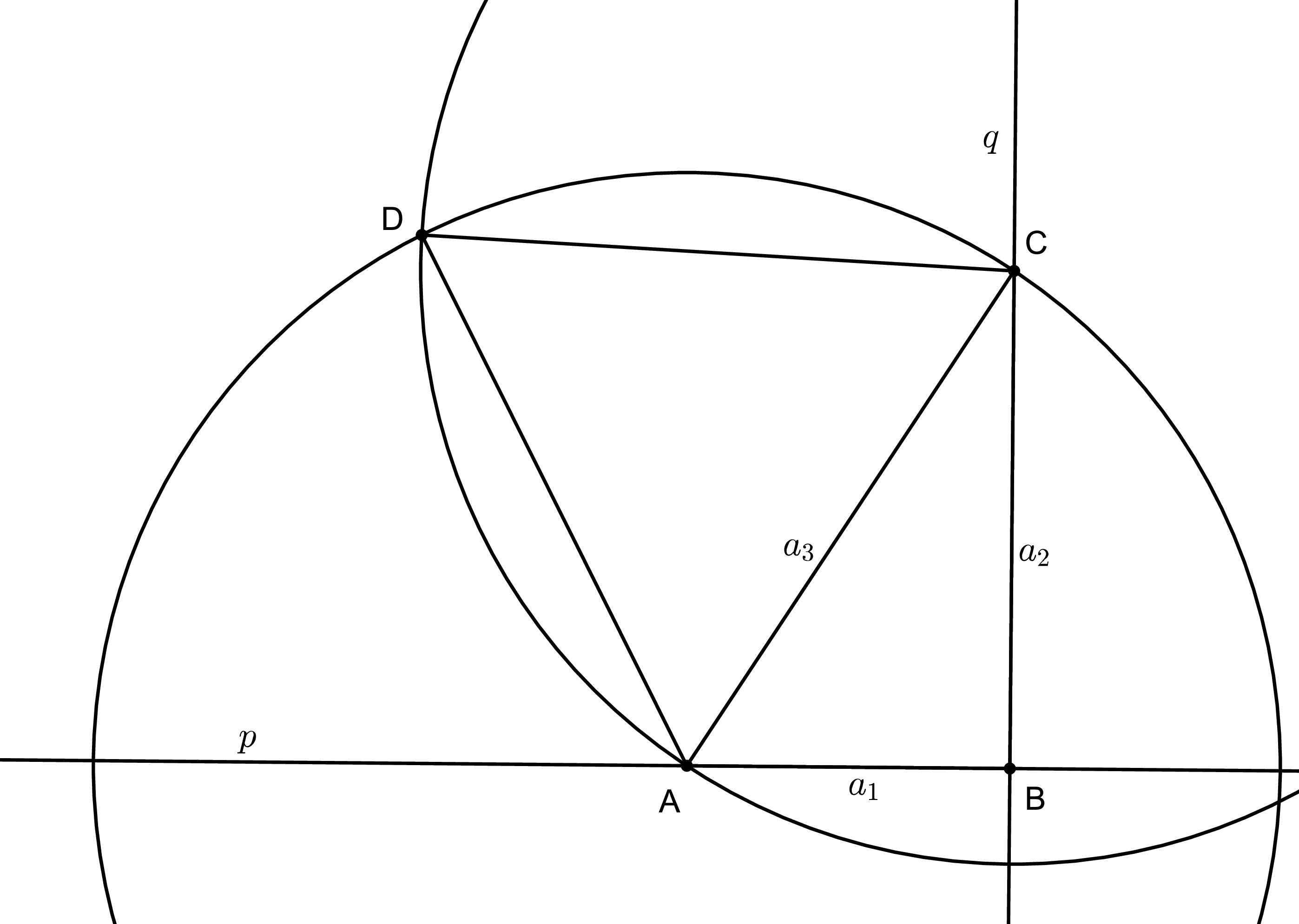
Ako prvé si teda spravme priamku \(p\) a prenesme na ňu dĺžku \(a_1\) - úsečka \(AB\). Teraz spravíme kolmicu na \(p\) cez bod \(B\) (priamka \(q\)). Na ňu prenesieme dĺžku \(a_2\) (úsečka \(BC\)) a nový bod \(C\) spojíme s bodom \(A\). Teraz sme dostali dĺžku \(a_3\) (úsečka \(AC\)). Na nájdenie zvyšného bodu trojuholníka so stranou \(a_3\) spravíme kružnice z krajných bodov úsečky \(AC\) s polomerom \(a_3\). Ich priesečník (bod \(D\)) bude zvyšným bodom hľadaného trojuholníka s obsahom \(S_1+S_2\). A máme hotovo.