Zadanie
Deti našli kalkulačku. Na začiatku naťukajú do kalkulačky číslo \(1\). V každom kroku si náhodne vyberú jedno z čísel \(3\), \(5\), \(8\), \(9\) (každé s rovnakou pravdepodobnosťou) a vynásobia ním číslo v kalkulačke. Tento krok potom opakujú, kým sa nedostanú k číslu, ktoré po delení \(13\) dáva zvyšok \(10\) alebo \(12\). Tarzanko sa stavil, že tento proces skončí na zvyšku \(10\), Janka si zas vybrala zvyšok \(12\). S akou pravdepodobnosťou vyhrá Tarzanko stávku1?
Kalkulačka nemá obmedzený počet cifier, teda dokáže zobraziť ľubovoľne veľké číslo.↩︎
Najprv urobíme niekoľko zaujímavých pozorovaní.
Nezaujíma nás konkrétne číslo na kalkulačke, iba jeho zvyšok po delení \(13\).
Nezaujímajú nás čísla, ktoré boli na kalkulačke v minulosti.1.
Nech \(p_{i}, 1 \leq i \leq 12\) je pravdepodobnosť, že ak sa práve teraz na kalkulačke nachádza číslo so zvyškom \(i\), Tarzanko niekedy v budúcnosti vyhrá. Našou úlohou je nájsť hodnotu \(p_{1}.\)
Zrejme \[p_{12} = 0,\quad p_{10} = 1.\] Nasledujúcim spôsobom vieme vyjadriť pravdepodobnosť \(p_i\) pomocou pravdepodobností čísel, ktoré sa na kalkulačka môžu objaviť v ďalšom kroku. Keď na kalkulačke je číslo \(i\), v nasledujúcom ťahu sa na kalkulačke môžu objaviť čísla \((3i, 5i, 8i, 9i)\), každé s pravdepodobnosťou jedna štvrtina. To, že Tarzanko vyhrá, sa môže stať jedným z nasledujúcich štyroch spôsobov: (ďalšie číslo na kalkulačke bude \(3i\) a Tarzanko vyhrá, ďalšie číslo na kalkulačke bude \(5i\) a Tarzanko vyhrá, …). Celková pravdepodobnosť \(p_i\) výhry Tarzanka je súčet pravdepodobností týchto štyroch udalostí. Ich pravdepodobnosti sú \[\left(\frac{1}{4}p_{3i},\ \frac{1}{4}p_{5i},\ \frac{1}{4}p_{8i},\ \frac{1}{4}p_{9i}\right).\]
Napríklad dostaneme
\[p_{1} = \frac{1}{4}(p_{3} + p_{5} + p_{8} + p_{9}).\]
Podobne \[p_{2} = \frac{1}{4}(p_{6} + p_{10} + p_{3} + p_{5})\] a analogicky vieme napísať rovnicu pre každé \(i, 1 \leq i \leq 12.\)
Tým dostávame sústavu \(10\) rovníc o \(10\) neznámych, ktorú stačí vyriešiť.
Následne zistíme \(p_{1} = \frac{21}{46} \approx 0.457\).
Bonus
Ešte si ukážeme ako šikovným spôsobom bolo možné znížiť počet neznámych. Hru zo zadania si možno predstaviť ako dvojrozmernú tabuľku na obrázku.
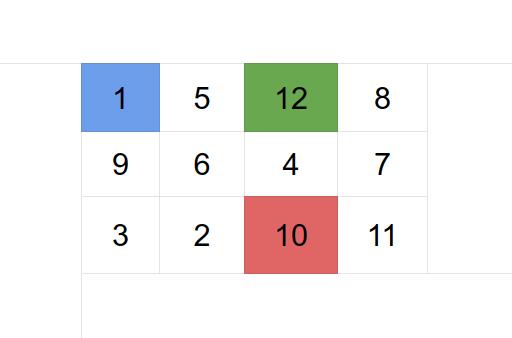
na začiatku hry sa nachádzame v ľavom hornom rohu
násobenie číslom \(3\) znamená krok smerom hore
násobenie číslom \(5\) znamená krok smerom vpravo
násobenie číslom \(8\) znamená krok smerom vľavo
násobenie číslom \(9\) znamená krok smerom dole
ak by sme mali urobiť krok mimo tabuľky, objavíme sa na opačnom konci tabuľky (ak sa nachádzame na čísle \(1\) a pôjdeme dohora, objavíme sa na čísle \(3\))
ak sa dostaneme na políčko s číslom \(10\) vyhral Tarzanko, ak na políčko s číslom \(12\) vyhrala Janka
Ďalej budeme políčka označovať iba číslami.
Pozorovania:
Rozhodujúce pozície \(10, 12\) sú symetricky uložené vzhľadom na každú z pozícií označených číslami \(9,\ 6,\ 4,\ 7\). To znamená \(p_{9} = p_{6} = p_{4} = p_{7} = \frac{1}{2}.\)
Pozícia rozhodujúcich políčok je voči \(1, 3\) zrkadlovo otočená (\(10\) má rovnakú pozíciu voči \(3\) ako \(12\) voči \(1\) a naopak). To znamená \(p_{1} = 1 - p_{3}\).
Podobné pozorovanie možno urobiť aj s dvojicami \((5, 2),\ (8, 11),\) teda \(p_{5} = 1 - p_{2},\ p_{8} = 1 - p_{11}\).
Týmto spôsobom je možné znížiť počet neznámych na \(3\) a stačí vyriešiť sústavu troch rovníc.
Procesy s touto vlastnosťou sa nazývajú Markovove, viac sem: https://en.wikipedia.org/wiki/Markov_chain↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.