Zadanie
Mišovia ši objednali pečené kuracie štehná š ryžou a kompótom. Tie ša však už minuli, tak ši Mišovia objednali pomaly pečené bravčové karé. To ša pečie tak pomaly, až ši Mišovia začali krátiť čaš hraním ša šo šervítkami.
Šervítok je \(n^2\), kde \(n > 1\) je prirodzené číšlo, a každá má tvar rovnoštranného trojuholníka šo štranou dĺžky \(1\). Navyše má každá z nich jednu z \(k\) farieb, kde \(1 < k < n^2\). Z každej farby je rovnako veľa šervítok. Mišovia z nich poškladali veľký rovnoštranný trojuholník šo štranou dĺžky \(n\). Napr. pre \(n=4\) by veľký trojuholník vyzeral takto:
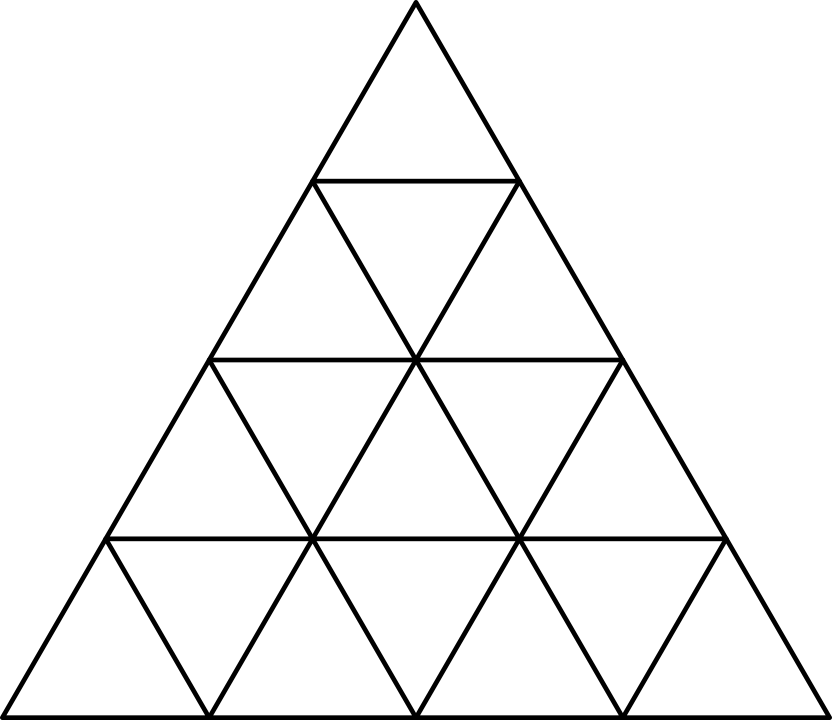
Keď boli hotoví, zištili, že nech ho ľubovoľne otočia (v rovine, kde trojuholník leží, teda bez zrkadlového preklopenia), pričom bude pokrývať tú ištú oblašť ako pôvodne, zafarbenie trojuholníka bude vyzerať štále rovnako. Určte všetky ušporiadané dvojice číšel \((n,\ k)\), pre ktoré ša taký trojuholník poškladať dá.
Zo zadania vieme, že počet servítok \(s\) je rovnaký pre každú z \(k\) farieb, teda musí platiť, že \(k \cdot s = n^2\), teda \(k \mid n^2\).
Všetky rotácie pravidelného trojuholníka v rovine (okolo ťažiska) sú práve tri otočenia \(\rho\): o \(120^\circ\), \(240^\circ\) a \(360^\circ = id\) čo sa nazýva aj identita, lebo nám to transformuje náš trojuholník do pôvodného stavu.
Poďme konštruovať náš trojuholník nasledovne. Keďže vieme, že trojuholník má vyzerať po každom otočení rovnako, tak vlastne môžeme poskladať jednu jeho tretinu, ktorou otočením o naše rotácie \(\rho\) dostaneme celý trojuholník, viď obrázok. Lenže máme dva typy trojuholníkov. Také ktoré majú \(3t\) častí, s tými nemáme problém, a také, ktoré majú \(3t +1\) častí.
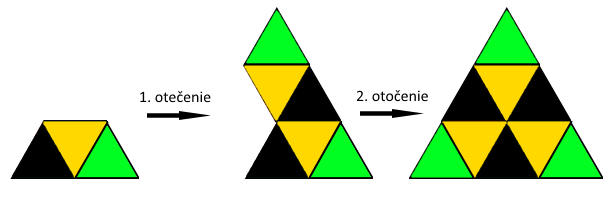
Lebo keď si rozdelíme všetky prirodzené čísla \(n\) podľa zvyškov po delení \(3\), teda zvyšky \(0\), \(1\) a \(2\), tak dostaneme, že \(n^2\) môže mať zvyšky len \(0\), \(1\): \[\begin{aligned} 0^2 = 0, && 1^2 = 1, && 2^2 = 4 \equiv 1. \end{aligned}\]
Ak \(n^2\) má zvyšok \(1\) po delení \(3\), vyfarbime \(x\) políčok (pre nejaké \(x\)) v jednej tretine jednou vybranou farbou, potom v ostatných tretinách musíme tiež vyfarbiť prislúchajúce políčka rovnako, a teda celkovo vyfarbených políčok bude \(3x\). Stredové políčko musí tiež byť zafarbené nejakou farbou menom \(\varphi\). Stredové políčko je jediné, ktoré sa zobrazí samo na seba, takže počet servítok farby \(\varphi\) bude \(3m+1\) (pre \(m \in \mathbb{N}\)), čo nie je deliteľné \(3\), takže sa to nemôže rovnať \(3x\). Máme dve farby s rôznymi počtami políčok, čo nemôže nastať, takže \(n\) musí byť deliteľné \(3\).
V našej počiatočnej tretine máme teraz presne \(\frac{n^2}{3}\) častí. Keďže počet servítok \(s\) je rovnaký v celom trojuholníku tak aj v jednej tretine, takže \(k\mid\frac{n^2}{3}\).
Naopak ak sú splnené podmienky \(3\) delí \(n\), \(n, k > 1\) a \(k\) delí \(\frac{n^2}{3}\), tak vieme trojuholník zafarbiť tak, aby vyzeral rovnako po každej rotácii. Spravíme to tak, že počiatočnú tretinu zafarbíme ľubovoľne tak, že v nej bude rovnako veľa políčok z každej farby a zvyšné dve tretiny zafarbíme príslušne podľa rotácií prvej tretiny. Teda takéto trojuholníky vieme vytvoriť pre také usporiadané dvojice \((n,k)\), kde platí, že \(3\mid n\), \(n, k > 1\) a \(k\mid\frac{n^2}{3}\). Príklady: \((3,3)\), \((6,3)\), \((6,4)\), \((6,6)\), \((6,12)\). To sa dá čarovne zapísať ako nižšie uvedená množina, no neľakajte sa jej, je to len iný zápis.
\[\left\{(n,k);\ n,k \in \mathbb{N},\ 3 \mid n ,\ n, k > 1,\ k\mid\frac{n^2}{3} \right\}\]
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.