Zadanie
Keďže Krtko zdolal skúšku ľavou zadnou, tak mu kráľ potajme hodil do vrecka príklad, ktorým sa už dlho trápil. Keď sa Krtko ospravedlnil, že sa pôjde prejsť do záhrady, rukou vo vrecku našmátral dáky papierik. Avšak nebol to žiaden zamilovaný odkaz, ale matematický príklad!
Máme danú priamku \(p\) a úsečku \(AB\), ktoré sa pretínajú v bode \(P\) rôznom od bodov \(A,B\). Navyše vzdialenosť bodu \(A\) od priamky \(p\) je dvakrát väčšia ako vzdialenosť bodu \(B\) od priamky \(p\). Zostrojte1 na priamke \(p\) body \(X\) a \(Y\) tak, aby bol trojuholník \(AXY\) rovnoramenný so základňou \(AY\) a zároveň aby priamka \(BX\) bola osou uhla \(AXY\).
Ak ste sa s podobným typom úloh ešte nestretli, môže vám pomôcť krátky text na stránke: https://kms.sk/ako_riesit/konstrukcne_ulohy/.↩︎
Chceme zostrojiť rovnoramenný trojuholník, o ktorom vieme, že os uhla \(AXY\) prechádza cez bod \(B\). Vieme, že množina bodov rovnako vzdialených od dvoch rôznych bodov je priamka, konkrétne os úsečky. Ďalej si môžeme všimnúť, že v rovnoramennom trojuholníku je táto os základne totožná s osou uhla oproti základni.
Konštrukcia: Spravíme kružnicu so stredom v bode \(B\) a s polomerom \(|AB|\). Tam, kde sa nám pretne s priamkou \(p\), dostaneme dva body, označme ich \(Y_1\) a \(Y_2\). Tieto teraz s spojíme s bodom \(A\) a s bodom \(B\). Dostávame dva rovnoramenné trojuholníky \(ABY_1\) a \(ABY_2\). Nech BUNV \(Y=Y_1\) (pre druhý z bodov je pokračovanie analogické).
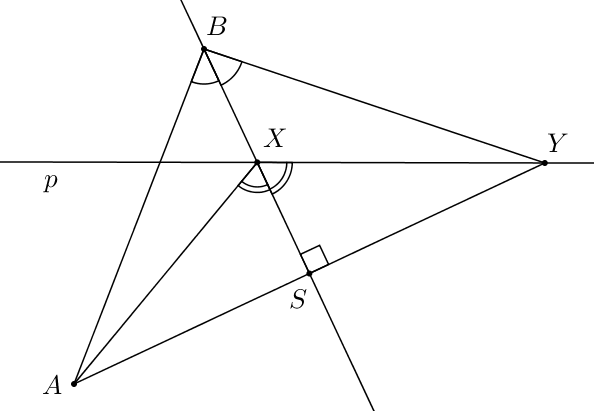
Teraz zostrojme os uhla \(ABY\). Táto os nám kolmo pretne základňu \(AY\) v jej strede, označme \(S\), a pretne sa aj s priamkou \(p\), označme \(X\). Môžeme si skontrolovať, že to naozaj je ten náš hľadaný bod \(X\). Keď spojíme \(A\) s \(X\), dostávame dva trojuholníky, \(AXS\) a \(XYS\), ktoré majú spoločnú jednu stranu \(XS\), rovnaký (pravý) uhol pri vrchole \(S\) a veľkosť úsečiek \(AS\) a \(SY\) je rovnaká, teda tieto trojuholníky sú zhodné. Nakoniec trojuholník \(AXY\) je rovnoramenný a priamka \(BX\) je osou strany \(AY\), a teda aj osou uhla \(AXY\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.