Zadanie
Pávovi sa zapáčila Krtkova čiapka, až ju uchmatol a odletel na neďaleký balkón. To Krtko však nemohol nechať tak, keďže to bola jeho obľúbená čiapka. Začal teda liezť na balkón po brečtane. Ako sa snažil prehupnúť cez zábradlie, zbadal Artušovu manželku Ginevru ako sa bozkáva s Lancelotom. To ho úplne vykoľajilo, až sa mu pošmykli ruky a zrúbal sa na zem. Hlava sa mu zakrútila až tak, že videl poletovať rovnice.
Nájdite všetky hodnoty reálneho parametra \(p\), pre ktorý má rovnica \[\bigg|\Big|20\left|x\right|-x^2\Big|-p\bigg|=21\] práve \(12\) rôznych koreňov.
V tejto úlohe si vcelku pekne vystačíme s geometrickou predstavou. Najprv si vieme všimnúť, že ak by parameter \( p \) bol mimo absolútnej hodnoty, tak by zvyšok funkcie posúval iba pozdĺž \( y \)-ovej osi – jednoducho by sme k funkcii prirátavali konštantu. Absolútna hodnota by to hádam nemusela veľmi zmeniť, tak poďme do úlohy s tým, že parameter sa dorieši nakoniec.
Ako by vyzerala naša funkcia bez parametra \( p \)?
Tak funkcia je potom vo forme: \[\bigg|\Big|20\cdot|x|- x^2\Big|\bigg| = \Big|20\cdot|x|- x^2\Big|.\] Je na nej úplne zlaté, že párna. Takže sa rovnako správa k záporným a kladným číslam. To vidíme, ak do nej napríklad dosadíme \( -x \): \[\Big|20\cdot|-x|- (-x)^2\Big| = \Big|20\cdot|x|- (x)^2\Big|.\] Vďaka tomu nám stačí pozerať sa iba na \( x \) kladné a správanie sa na záporných číslach dostaneme symetriou podľa \( y \)-ovej osi. Na nezáporných číslach nám vnútorná absolútna hodnota nič nerobí (však na to sme to robili), a teda dostávame už pekne sa mračiacu konkávnu parabolu: \[|20\cdot x - x^2| = |x\cdot(20-x)|.\]

Tak naša parabola má priesečníky s \( x \)-ovou osou v bodoch \( x = 20 \) a \( x = 0 \). Tiež si teraz vieme vypočítať, kde je a akú má hodnotu vo vrchole – parabola je symetrická aspoň na intervale \(\) to platí aj pre našu. Potom teda je jej vrchol v strede medzi priesečníkmi a nadobúdame v ňom hodnotu \(|10\cdot(20-10)| = 100\). Super, tak máme dobrú predstavu, ako vyzerá naša parabola na kladnom definičnom obore. Celá je ešte v absolútnej hodnote, tak záporné funkčné hodnoty zobrazme do kladnej polroviny podľa osi \( x \). Tým dostávame červenú krivku na obrázku vyššie (všimnite si, ako sa záporné hodnoty paraboly znázornené svetlou červenou preklopili cez \( x \)-ovú os do kladných). Nakoniec záporné čísla dokončíme vďaka parite našej funkcie a dostávame nasledujúci obrázok:
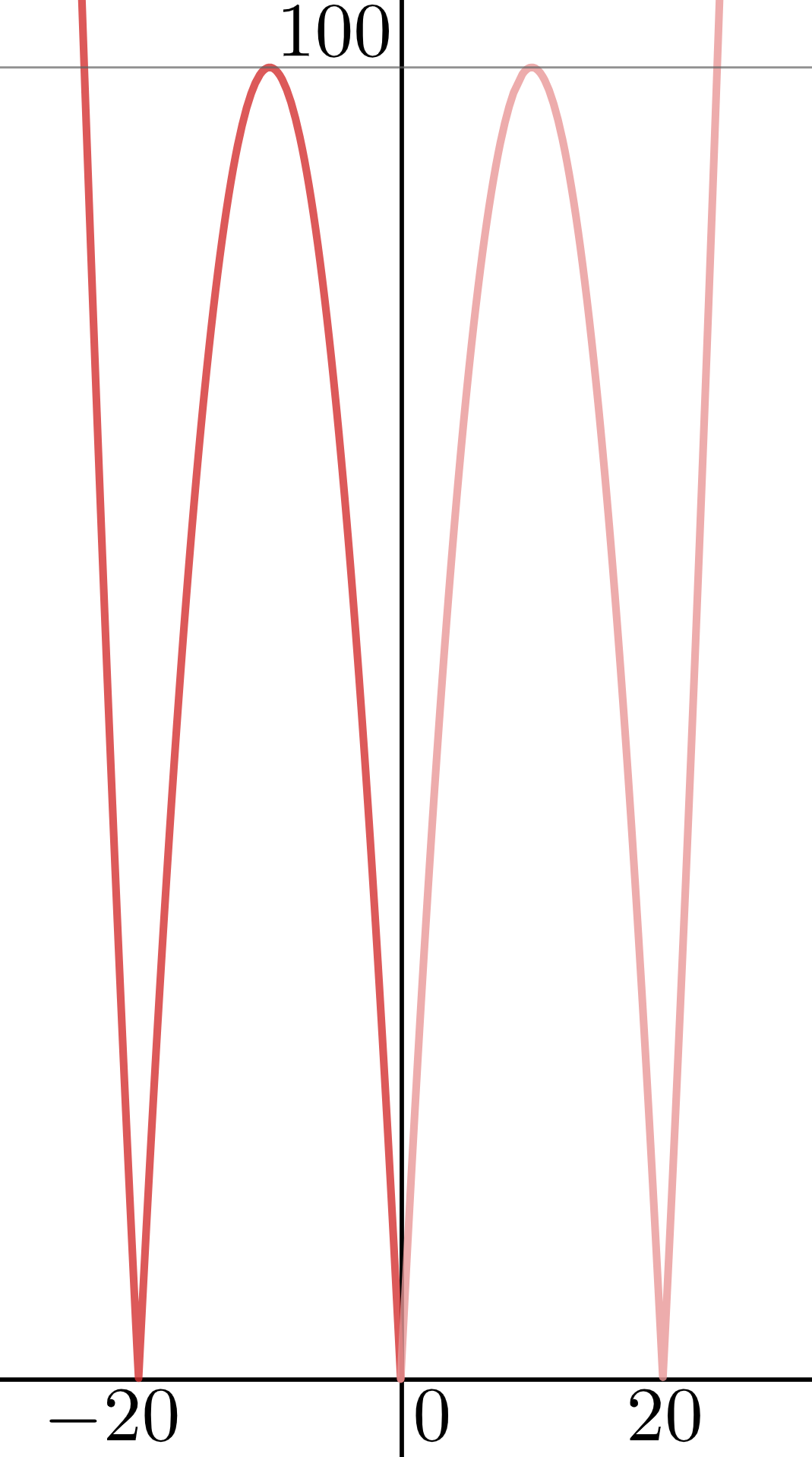
Tak a teraz je najvyšší čas sa pozrieť do zadania a zistiť, čo od nás vlastne chce – aký má byť parameter, aby rovnica \[\bigg|\Big|20\cdot|x|- x^2\Big|-p\bigg| = 21\] mala práve \( 12 \) koreňov? To však neznamená nič iné, ako to, že naša funkcia má mať \( 12 \) priesečníkov s konštantnou čiarou \( y = 21 \). Teraz ako je, tak má s každou konštantou maximálne \( 6 \) priesečníkov. Avšak, mágia príde s parametrom. Ako postupne meníme hodnotu parametra, tak funkcia sa nám posúva hore a dole pozdĺž osi \( y \) a následne sa nám záporné hodnoty preklápajú na kladné.
Uvedomme, si že na zistenie počtu priesečníkov s hodnotou \( 21 \) nám stačí zistiť počet priesečníkov funkcie bez absolútnej hodnoty s hodnotami \( 21 \) a \( -21 \). Jednoducho každý priesečník s \( -21 \) sa nám zobrazí na priesečník, ktorý nás zaujíma (\( 21 \)). Potom však parameter naozaj nerobí nič iné ako to, že funkciu posúva nižšie a vyššie. Naša funkcia bez vonkajšej absolútnej hodnoty nadobúda každú hodnotu maximálne \( 6 \)-krát, a teda jedna šestica bude musieť pretnúť \( 21 \) a druhá \( -21 \). Takže potrebujeme, aby \[100 - p > 21,\] lebo potrebujeme, aby bol vrchol paraboly nad hodnotou \( 21 \) a zároveň \[0 - p < -21,\] aby najmenšia hodnota na parabole pretla \( -21 \).
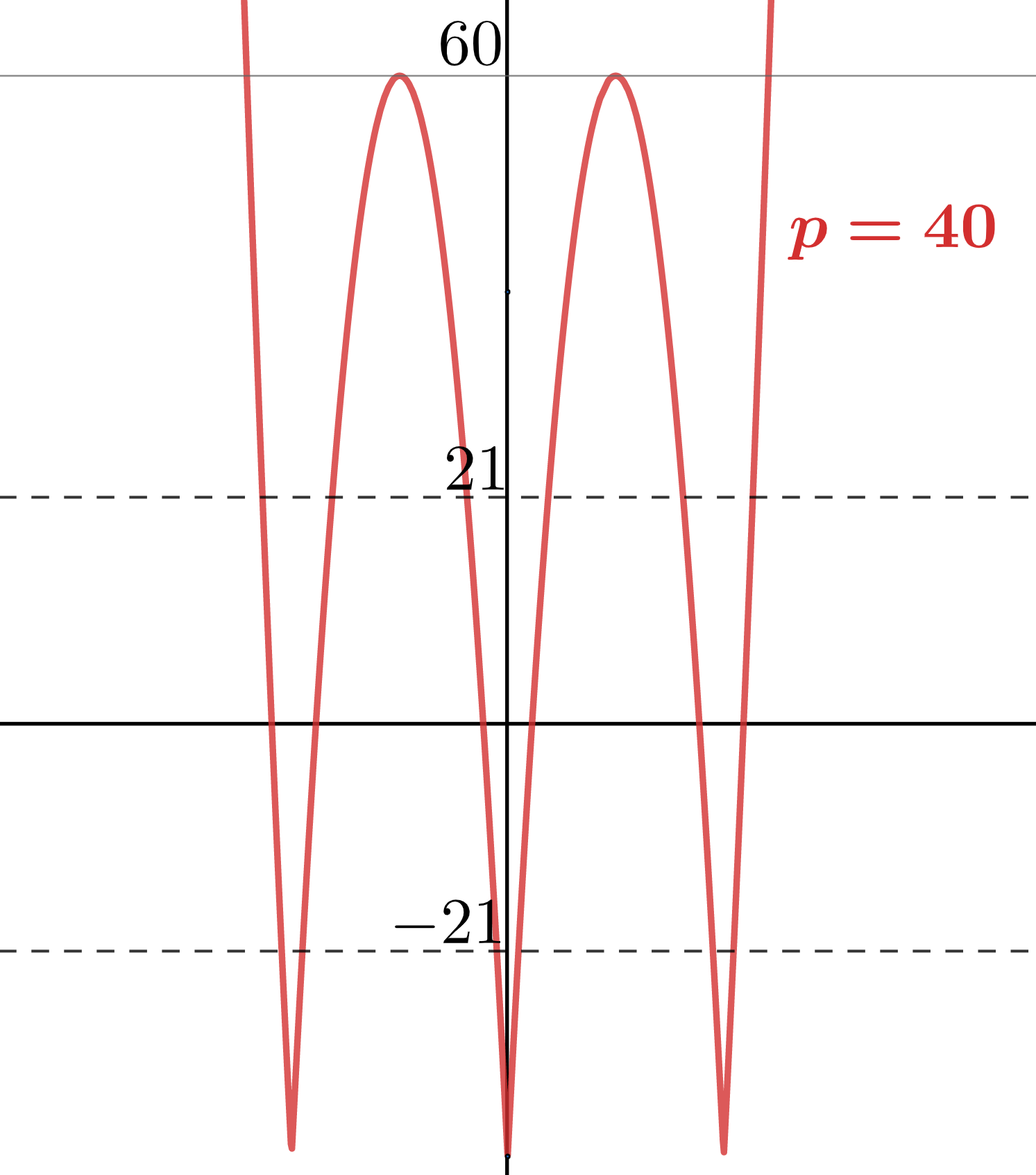
A teda \( p \in(21,79) \).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.