Zadanie
Keď sa preberie, vidí Ginevru a Lancelota, ktorí sa nad ním skláňajú. Ginevra sa podujme mu vysvetľovať, že kujú spolu pikle. Na čo sa Krtko ohradí, že on s tým nechce mať nič spoločné, avšak Lancelot ho nepočúva a zavrie ho do kumbálu na metly. Tu si Krtko smutne povzdychne, že azda mu sú metly súdené. Všimne si však vitrážové okno, na ktorom je množstvo trojuholníkov.
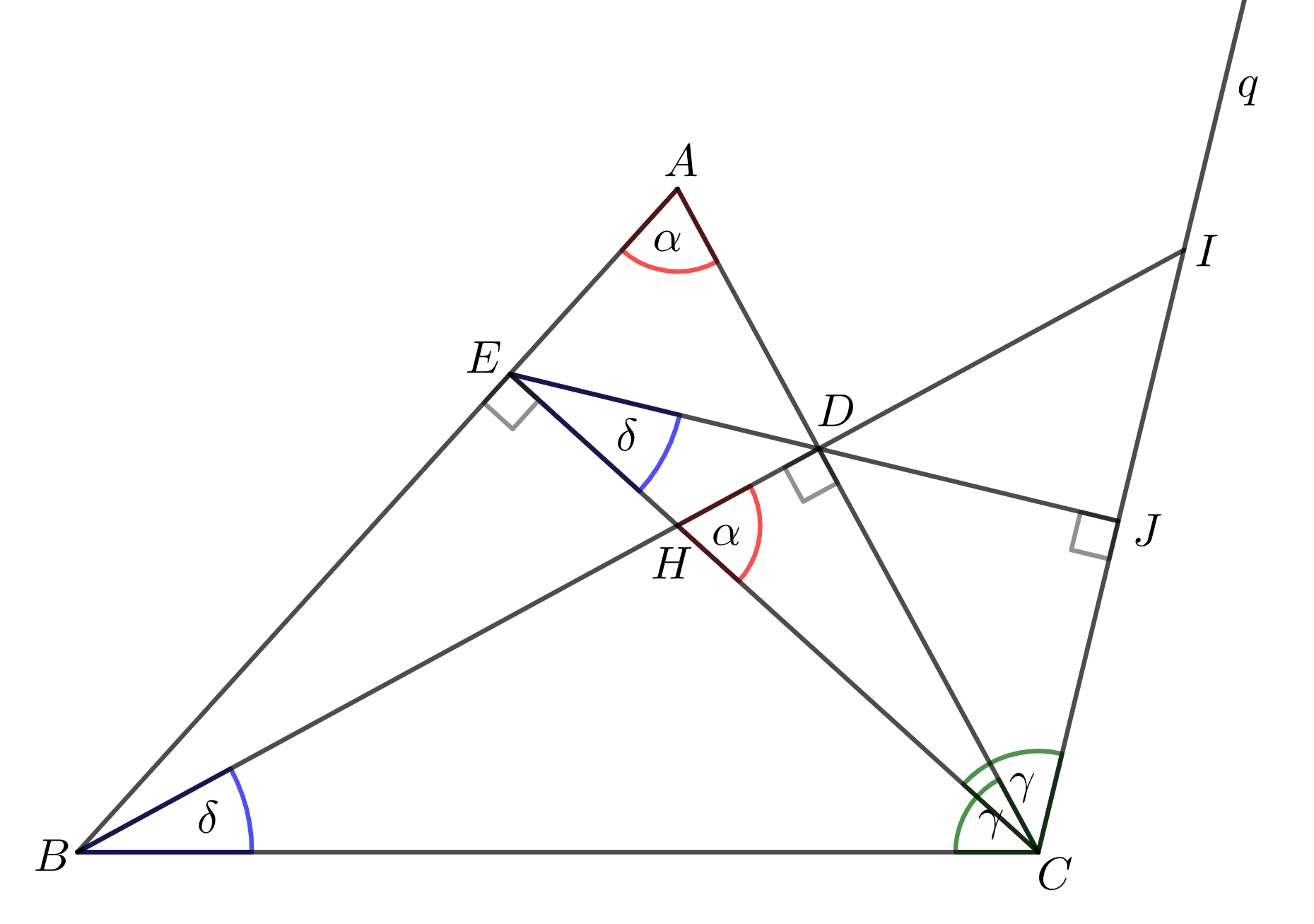
V ostrouhlom trojuholníku \(ABC\) označme \(D,\, E\) postupne päty výšok z vrcholov \(B,\, C\) a priesečník týchto výšok označme \(H\). Nech \(q\) je kolmica z vrcholu \(C\) na priamku \(DE\) a \(I\) je priesečník \(q\) s priamkou \(BD\). Dokážte, že trojuholníky \(HIC\) a \(ABC\) sú podobné.
Načrtnime si situáciu zo zadania a označme si priesečník priamky \(q\) a priamky \(DE\) ako \(J\).
Trojuholníky \(AEC\) a \(HDC\) sú podobné, keďže majú jeden pravý uhol a jeden spoločný uhol \(ACE=DCH\). Tým pádom aj uhly \(EAC\) a \(CHD\) sú rovnako veľké. \[|\sphericalangle EAC|=|\sphericalangle CHD|=\alpha\]
Štvoruholník \(BCDE\) je tetivový, nakoľko uhly \(BDC\) a \(BEC\) sú oba pravé a ležia nad rovnakou tetivou \(BC\). Tým pádom aj uhly \(CED\) a \(CBD\) majú rovnakú veľkosť, nakoľko ležia nad rovnakou tetivou \(CD\). \[|\sphericalangle CED|=|\sphericalangle CBD|=\delta\]
Trojuholníky \(BCD\) a \(ECJ\) sú podobné, nakoľko oba majú jeden uhol pravý a jeden veľkosti \(\delta\). Z toho vyplýva, že uhly \(BCD\) a \(ECJ\) sú tiež rovnako veľké. \[|\sphericalangle BCD|=|\sphericalangle ECJ|=\gamma\]
Posledne už vieme dokázať, že trojuholníky \(HIC\) a \(ABC\) sú podobné, nakoľko oba majú dva uhly rovnakej veľkosti. \[|\sphericalangle CHI|=|\sphericalangle BAC|=\alpha\qquad|\sphericalangle ICH|=|\sphericalangle ACB|=\gamma\]
Komentár
Na rovnosť uhlov \(CED\) a \(CBD\) je možné prísť aj bez použitia tetivových štvoruholníkov. Stačí si za pomoci vrcholových uhlov pri vrchole \(H\) všimnúť, že trojuholníky \(EBH\) a \(DCH\) sú podobné, keďže majú dva uhly rovnakej veľkosti. Tým pádom sú pomery strán \(EH\) a \(DH\) rovné pomeru strán \(BH\) a \(CH\).
Následne vieme o trojuholníkoch \(BCH\) a \(EDH\) povedať, že sú podobné, pretože majú jeden vrcholový uhol rovnakej veľkosti a pomery dvoch strán sú rovné. Tým pádom dostávame hľadanú rovnosť uhlov \(CED\) a \(CBD\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.