4. Kúpim Myši Syr $\left(\kappa \le 5\right)$ vzorové riešenie

Aby sme ukázali, že trojuholníky \(MY\check S\) a \(SYR\) sú podobné, potrebujeme najprv ukázať, že majú rovnaké vnútorné uhly. Očakávame, že \(|\sphericalangle YRS|=|\sphericalangle Y\check SM|\), \(|\sphericalangle RSY|=|\sphericalangle \check SMY|\) a \(|\sphericalangle SYR|=|\sphericalangle MY\check S|\).

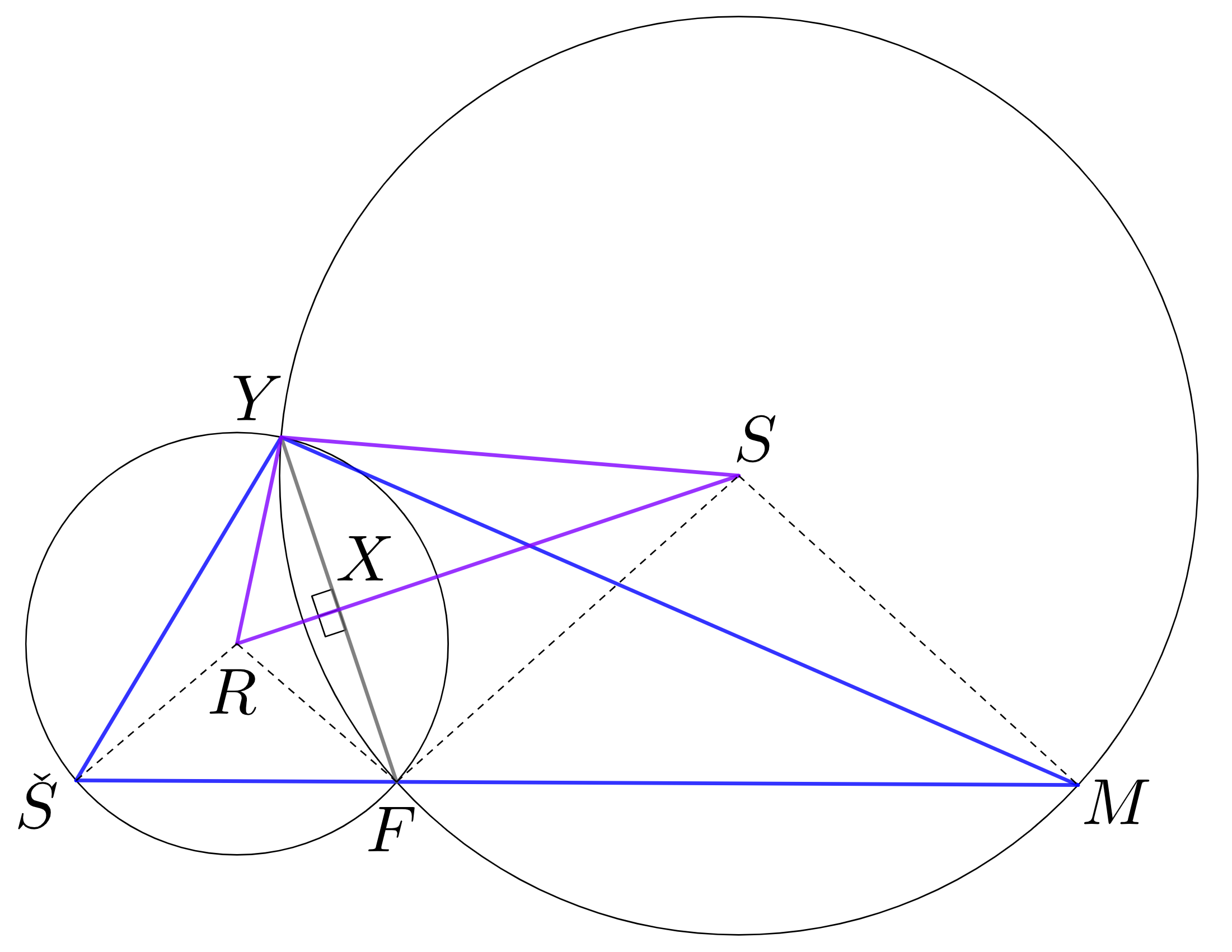
Na začiatok si spojme \(Y\) a \(F\), ktoré tvoria jedinú spoločnú tetivu oboch kružníc, ktorá je zároveň kolmá na spojnicu stredov kružníc \(RS\). To vieme pretože stred opísanej kružnice leží na osiach strán, zároveň oba stredy musia ležať na osi \(YF\), teda ich spojnica leží na osi \(YF\). Ich priesečník si označíme ako bod \(X\). Skúsme sa teraz pozrieť na trojuholník \(FY\check S\) a ukázať z neho \(|\sphericalangle YRS|=|\sphericalangle Y\check SM|\).

Spojíme si všetky vrcholy trojuholníka \(\check SFY\) so stredom kružnice \(R\).

Trojuholníky \(Y\check SR\), \(\check SFR\), \(FYR\) sú všetky rovnoramenné, teda aj ich uhly pri základni budú rovnaké. Z trojuholníka \(YRX\) vyplýva \[\begin{align} 90^\circ + \textcolor[RGB]{0, 255, 255}{\sphericalangle} + \textcolor[RGB]{000, 255, 000}{\sphericalangle} &= 180^\circ,\\ \textcolor[RGB]{0, 255, 255}{\sphericalangle} + \textcolor[RGB]{000, 255, 000}{\sphericalangle} &= 90^\circ,\\ \textcolor[RGB]{0, 255, 255}{\sphericalangle} &= 90^\circ - \textcolor[RGB]{000, 255, 000}{\sphericalangle}.\end{align}\] Z trojuholníka \(\check SFY\) vieme, že \[2\textcolor[RGB]{255, 000, 000}{\sphericalangle} + 2\textcolor[RGB]{000, 000, 255}{\sphericalangle} + 2\textcolor[RGB]{000, 255, 000}{\sphericalangle} = 180^\circ,\] čo môžeme vykrátiť dvomi a dostaneme \[\begin{align} \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 000, 255}{\sphericalangle} + \textcolor[RGB]{000, 255, 000}{\sphericalangle} &= 90^\circ,\\ \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 000, 255}{\sphericalangle} &= 90^\circ - \textcolor[RGB]{000, 255, 000}{\sphericalangle}.\end{align}\] Spojením s predchádzajúcou rovnicou dostaneme \[\begin{align} \textcolor[RGB]{0, 255, 255}{\sphericalangle} &= 90^\circ - \textcolor[RGB]{000, 255, 000}{\sphericalangle} = \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 000, 255}{\sphericalangle},\\ \textcolor[RGB]{0, 255, 255}{\sphericalangle} &= \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 000, 255}{\sphericalangle}.\end{align}\] Ukázali sme teda, že platí rovnosť \(|\sphericalangle YRS|=|\sphericalangle Y\check SM|\).

To, že uhol, pod ktorým sa na tetivu pozeráme zo stredu je dvojnásobkom toho, pod ktorým sa na ňu pozeráme z nejakého bodu na kružnici, je však celkom silná a často používaná vlastnosť. Ide o takzvaný stredový a obvodový uhol. Skúsme sa teda na to pozrieť z tohto uhla. Môžeme si všimnúť, že \(\sphericalangle Y\check SF\) je obvodový ku \(\sphericalangle YRF\), a teda platí rovnosť \(|\sphericalangle YRF|=2|\sphericalangle Y\check SF|\).

Zároveň vieme, že \(RX\) je os \(\sphericalangle YRF\), keďže trojuholník \(RFY\) je rovnoramenný (\(|RY|=|RF|\), keďže sú to polomery). Potom ale vieme, že \(RS\) nám delí \(\sphericalangle YRF\) na polovicu, a teda platí rovnosť \(|\sphericalangle YRF|=2|\sphericalangle YRX|\).

Ak spojím tieto dve rovnosti dohromady, dostávam \(2|\sphericalangle YRX|=2|\sphericalangle Y\check SF|\), čo viem upraviť na \(|\sphericalangle Y\check SF|=|\sphericalangle YRX|\), čo je ekvivalentné s rovnosťou \(|\sphericalangle YRS|=|\sphericalangle Y\check SM|\).

Analogicky, i keď trochu inak sa pokúsime ukázať rovnosť \(|\sphericalangle RSY|=|\sphericalangle \check SMY|\).

Znovu si spojíme všetky vrcholy trojuholníka \(FMY\) so stredom kružnice \(S\).

Trojuholníky \(YMS\), \(YFS\), \(FMS\) sú všetky rovnoramenné, teda aj ich uhly pri základni budú rovnaké. Z trojuholníka \(YXS\) vyplýva \[\begin{align} 90^\circ + \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{0, 255, 255}{\sphericalangle} &= 180^\circ,\\ \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{0, 255, 255}{\sphericalangle} &= 90^\circ,\\ \textcolor[RGB]{0, 255, 255}{\sphericalangle} &= 90^\circ - \textcolor[RGB]{255, 000, 000}{\sphericalangle}. \end{align}\] Z trojuholníka \(\check YFM\) vieme, že \[\begin{align} (\textcolor[RGB]{255, 000, 000}{\sphericalangle} - \textcolor[RGB]{000, 000, 255}{\sphericalangle}) + (\textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 255, 000}{\sphericalangle}) + (\textcolor[RGB]{000, 255, 000}{\sphericalangle} - \textcolor[RGB]{000, 000, 255}{\sphericalangle}) &= 180^\circ,\\ 2\textcolor[RGB]{255, 000, 000}{\sphericalangle} + 2\textcolor[RGB]{000, 255, 000}{\sphericalangle} - 2\textcolor[RGB]{000, 000, 255}{\sphericalangle} &= 90^\circ, \end{align}\] čo môžeme vykrátiť dvomi a dostaneme \[\begin{align} \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 255, 000}{\sphericalangle} - \textcolor[RGB]{000, 000, 255}{\sphericalangle} &= 90^\circ,\\ \textcolor[RGB]{000, 255, 000}{\sphericalangle} - \textcolor[RGB]{000, 000, 255}{\sphericalangle} &= 90^\circ - \textcolor[RGB]{255, 000, 000}{\sphericalangle}.\end{align}\] Spojením s predchádzajúcou rovnicou dostaneme \[\begin{align} \textcolor[RGB]{000, 255, 000}{\sphericalangle} - \textcolor[RGB]{000, 000, 255}{\sphericalangle} &= 90^\circ - \textcolor[RGB]{255, 000, 000}{\sphericalangle} = \textcolor[RGB]{0, 255, 255}{\sphericalangle},\\ \textcolor[RGB]{000, 255, 000}{\sphericalangle} - \textcolor[RGB]{000, 000, 255}{\sphericalangle} &= \textcolor[RGB]{0, 255, 255}{\sphericalangle}.\end{align}\] Ukázali sme teda, že platí rovnosť \(|\sphericalangle RSY|=|\sphericalangle \check SMY|\).

Alebo sme si všimli, že \(\sphericalangle FMY\) je obvodový ku stredovému \(\sphericalangle FSY\) a analogicky vyvodili rovnosť \(|\sphericalangle YSX|=|\sphericalangle YMF|\), ktorá je ekvivalentná s rovnosťou \(|\sphericalangle RSY|=|\sphericalangle \check SMY|\).

Ukázali sme rovnosť dvoch vnútorných uhlov trojuholníkov \(MY\check S\) a \(SYR\). Z vety \(uu\) o podobnosti trojuholníkov vyplýva, že trojuholníky \(MY\check S\) a \(SYR\) sú podobné.

Avšak podobnosť trojuholníkov \(MY\check S\) a \(SYR\) sme nemuseli dokazovať práve cez rovnosti \(|\sphericalangle YRS|=|\sphericalangle Y\check SM|\), \(|\sphericalangle RSY|=|\sphericalangle \check SMY|\) – jednu z nich sme mohli nahradiť rovnosťou \(|\sphericalangle SYR|=|\sphericalangle MY\check S|\). Skúsme sa teraz na ňu pozrieť.

Môžeme si všimnúť, že \(\sphericalangle \check SFY\) je obvodový ku stredovému \(\sphericalangle \check SRY\), a teda platí rovnosť \(|\sphericalangle \check SRY|=2|\sphericalangle \check SFY|\). Rovnako aj \(\sphericalangle YFM\) je obvodový ku \(360^\circ - \sphericalangle YSM\), a teda platí rovnosť \(360^\circ -|\sphericalangle YSM|=2|\sphericalangle YFM|\).

Vieme, že \[\begin{align} \textcolor[RGB]{255, 000, 000}{\sphericalangle} + \textcolor[RGB]{000, 255, 000}{\sphericalangle} &= 180^\circ,\\ 2\textcolor[RGB]{255, 000, 000}{\sphericalangle} + 2\textcolor[RGB]{000, 255, 000}{\sphericalangle} &= 360^\circ,\\ 2\textcolor[RGB]{000, 255, 000}{\sphericalangle} &= 360^\circ - 2\textcolor[RGB]{255, 000, 000}{\sphericalangle},\\ |\sphericalangle YSM| &= 360^\circ - 2\textcolor[RGB]{255, 000, 000}{\sphericalangle},\\ |\sphericalangle YSM| &= 2\textcolor[RGB]{000, 255, 000}{\sphericalangle}.\end{align}\] Keďže sú oba trojuholníky \(YSM\) a \(YR\check S\) rovnoramenné s rovnakým uhlom oproti základni, tak budú mať rovnaké uhly aj pri základni, takže \(|\sphericalangle \check SYR|=|\sphericalangle MYS|\), z čoho vyplýva \(|\sphericalangle SYR|=|\sphericalangle RYM|+|\sphericalangle MYS|=|\sphericalangle \check SYR|+|\sphericalangle RYM|=|\sphericalangle MY\check S|\).

Teraz sa ostáva ešte zamyslieť ako by vyzeralo riešenie, ak by sme si bod \(F\) umiestnili niekde inde. Ak by sa \(F\) posunulo bližšie k \(\check S\), tak by sa mohlo stať, že by \(R\) ležalo mimo trojuholníka \(\check SMY\) a \(S\) vo vnútri alebo pod \(M\check S\). Ešte vieme \(F\) posunúť bližšie ku \(M\), v takom prípade by \(S\) ležalo mimo trojuholníka \(\check SMY\) a \(R\) pod \(M\check S\). V takomto prípade by postup riešenia vyzeral analogicky ku našej konfigurácií (resp. by sme vymenili metódy postupu pre jednotlivé uhly, keďže uhly sa nám preklopia na doplnok do \(180^\circ\) resp. \(360^\circ\)). Ak by sme \(F\) umiestnili do päty výšky na stranu \(\check SM\), tak by body \(R\), \(S\) postupe ležali na stranách \(\check SY\), \(MY\) a \(RS\) by bolo rovnobežné s \(\check SM\). Jednalo by sa teda o triviálny prípad. Ešte na konfiguráciu môže mať vplyv pôvodný trojuholník \(MY \check S\), avšak aj tu budeme postupovať analogicky, keďže sa nám len preklopia niektoré uhly.