2. Krásne Máme Servítky $\left(\kappa \le 2\right)$ vzorové riešenie

Zadanie

Keď sa David osprchoval, išiel sa so svojou partiou naraňajkovať do najbližšej Blagovgradskej jedálne. Kým čakali na svoje jedlo, Nina si všimla, že na stole stojí jedna modrá a jedna zelená váza, pričom obe majú štvorcovú podstavu. Taktiež boli na stole dve servítky zložené do zhodných rovnoramenných pravouhlých trojuholníkov. Jednotlivé vázy sa dali na tieto servítky položiť tak, ako na obrázku 1. Ďalej Nina zistila, že podstava väčšej vázy má stranu dlhú \(\SI{21}{\centi\metre}\). Vedeli by ste z toho zistiť, ako veľkú stranu mala podstava menšej vázy?

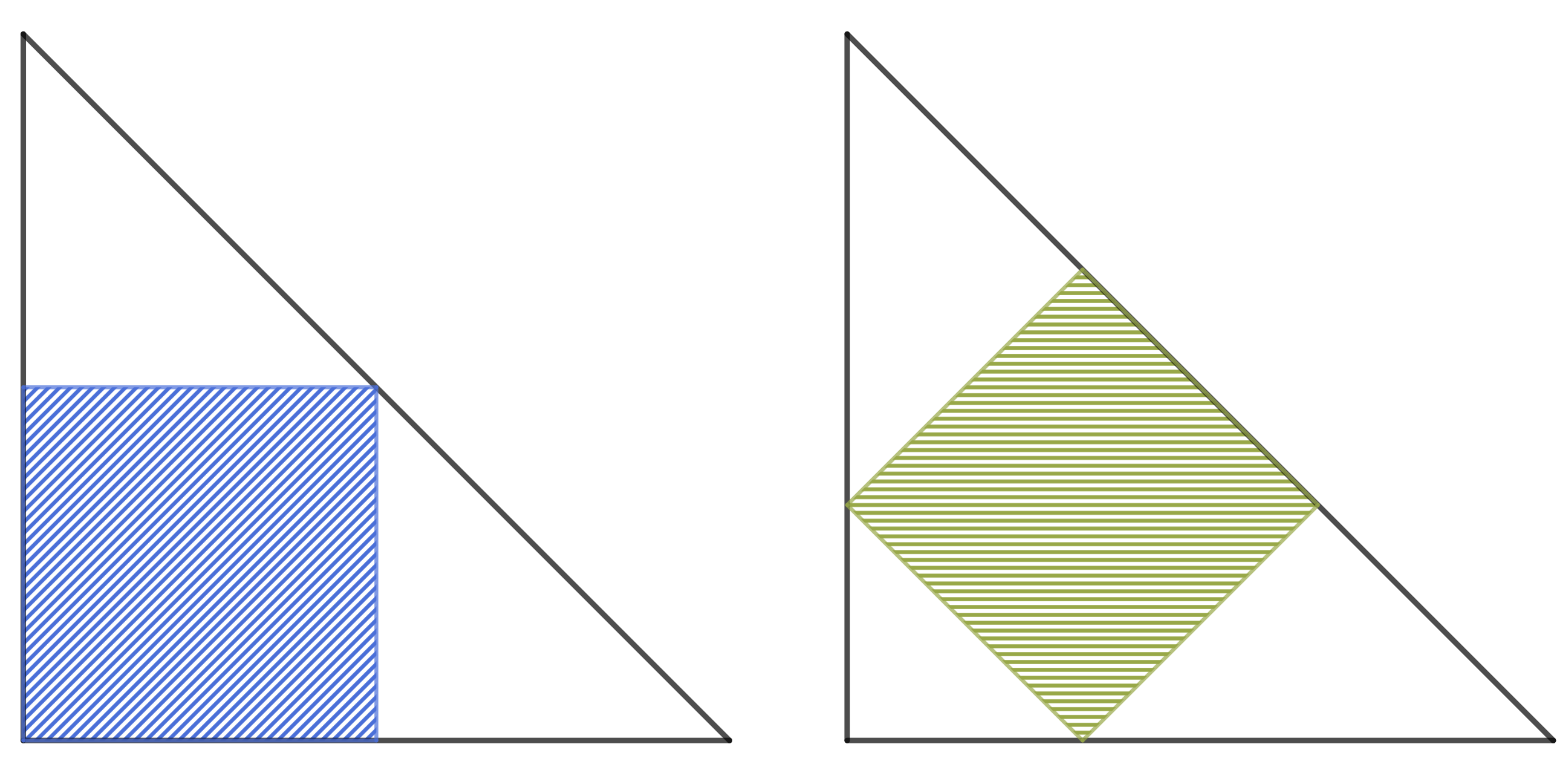
Nazvime si našu trojuholníkovú servítku ako \(ABC\) a dĺžku jej strany \(AB\) označme ako \(a\), modrú vázu ako \(W_1X_1Y_1Z_1\) a zelenú vázu ako \(W_2X_2Y_2Z_2\).

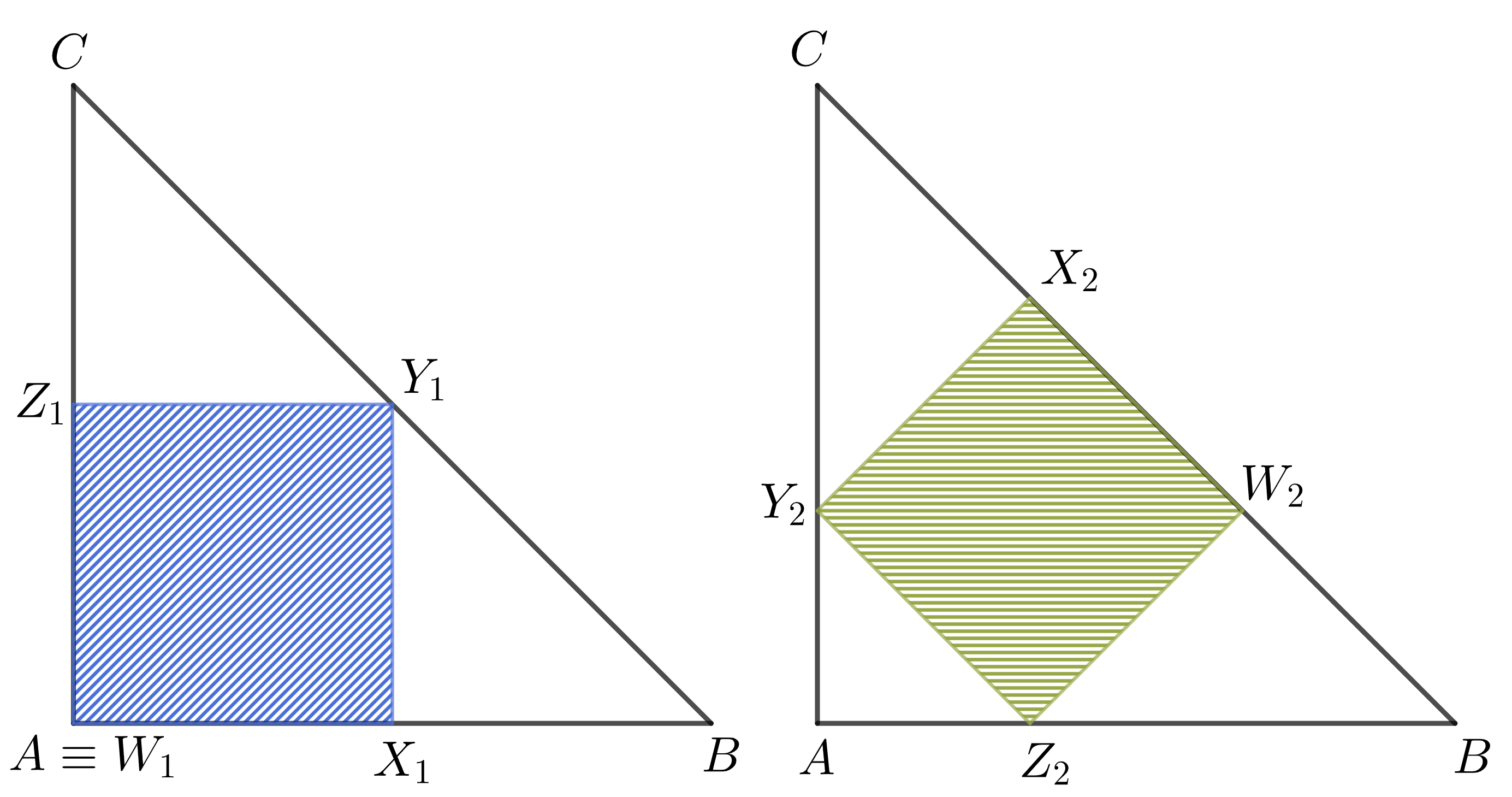
Na začiatok sa pozrime na modrú vázu. Keďže \(\sphericalangle ABC\) a \(\sphericalangle X_1BY_1\) je ten istý uhol a \(|\sphericalangle BAC|=|\sphericalangle BX_1Y_1|=90^\circ\), tak trojuholníky \(\triangle ABC\) a \(\triangle X_1BY_1\) sú podobné. Preto aj trojuholník \(\triangle X_1BY_1\) je rovnoramenný, čiže \(|BX_1|=|X_1Y_1|\). O váze ale vieme, že je štvorcová, čiže \(|AX_1|=|W_1X_1|=|X_1Y_1|\). Dokopy z toho dostávame, že \(|AX_1|=|X_1Y_1|=|BX_1|\), a teda, že \(X_1\) je stredom úsečky \(AB\). Potom už ale jasne vidíme, že strana modrého štvorca je \(m=\frac a2\).

Teraz sa povenujme zelenej váze. Keďže \(\sphericalangle ABC\) a \(\sphericalangle W_2BZ_2\) je ten istý uhol a \(|\sphericalangle BAC|=|\sphericalangle BW_2Z_2|=90^\circ\), tak trojuholníky \(\triangle ABC\) a \(\triangle W_2BZ_2\) sú podobné. To ale znamená aj, že trojuholník \(\triangle W_2BZ_2\) je rovnoramenný, čiže \(|BW_2|=|W_2Z_2|\). Rovnakým postupom na opačnom konci trojuholníka \(ABC\) sa vieme presvedčiť, že \(|CX_2|=|X_2Y_2|\). Z toho, že váza je štvorec, ďalej vieme \(|W_2Z_2|=|W_2X_2|=|X_2Y_2|\). Teraz však môžeme použiť naše rovnoramenné trojuholníky, z čoho dostaneme, že \(|BW_2|=|W_2X_2|=|CX_2|\), čiže \(W_2,X_2\) nám úsečku \(BC\) rozdeľujú na tretiny. Aká je však jej dĺžka? Úsečka \(BC\) je preponou v pravouhlom rovnoramennom trojuholníku \(ABC\) s dĺžkou odvesny \(a\). Môžeme teda použiť Pytagorovu vetu, z ktorej dostaneme \[|BC|^2=|AB|^2+|AC|^2=a^2+a^2=2a^2\implies|BC|=\sqrt{2a^2}=\sqrt2a.\] Nuž a keďže \(W_2X_2\) tvorí tretinu úsečky \(BC\), tak strana zeleného štvorca je \(z=\frac{\sqrt2}{3}a\).

Stále však nevieme, ktorá z váz má dlhšiu stranu. Zistíme to tak, že si ich dáme do nerovnosti, v ktorej nepoznáme znamienko, a tú budeme ekvivalentnými úpravami upravovať až do momentu, kedy to budeme vedieť určiť.

\[\begin{align} m&\stackrel{?}{\lessgtr}z,\\ \frac a2&\stackrel{?}{\lessgtr}\frac{\sqrt2}{3}a,\tag*{$\big/\ \div a$}\\ \frac12&\stackrel{?}{\lessgtr}\frac{\sqrt2}3,\tag*{$\big/\ ^2$}\\ \frac14&\stackrel{?}{\lessgtr}\frac29,\tag*{$\big/\ \cdot36$}\\ 9&>8.\end{align}\] Tu ešte treba zdôrazniť, že umocnenie je ekvivalentnou úpravou preto, že obe strany nerovnosti sú kladné. Ak by niektorá z nich bola záporná, umocnenie nám jej platnosť vie pokaziť (napr. z \(-3<2\) by sme dostali \(9<4\), čo očividne neplatí).

Dostali sme teda, že modrá váza je väčšia. Preto platí \(\SI{21}{\centi\metre}=m=\frac a2\), z čoho máme, že \(a=\SI{42}{\centi\metre}\). Strana menšej vázy je potom ale \(z=\frac{\sqrt2}{3}a=\frac{\sqrt2}{3}\cdot\SI{42}{\centi\metre}=14\sqrt2\ \si{\centi\metre}\).

Poznámka

Viacerí z vás ste automaticky prehlásili, že modrá váza je väčšia ako zelená (resp. že modrá váza má stranu dlhú ako \(\SI{21}{\centi\metre}\)) bez toho, aby ste to zdôvodnili. V zadaní však toto nijak zaručené nebolo. To, že ako prvá bola v zadaní spomenutá väčšia váza a na obrázku bola prvá (t. j. naľavo) modrá váza, ešte neznamená, že modrá musí byť väčšia. Pokojne sme ten obrázok mohli dať aj naopak. Potom by asi oveľa väčšiemu počtu z Vás vyšiel nesprávny výsledok.

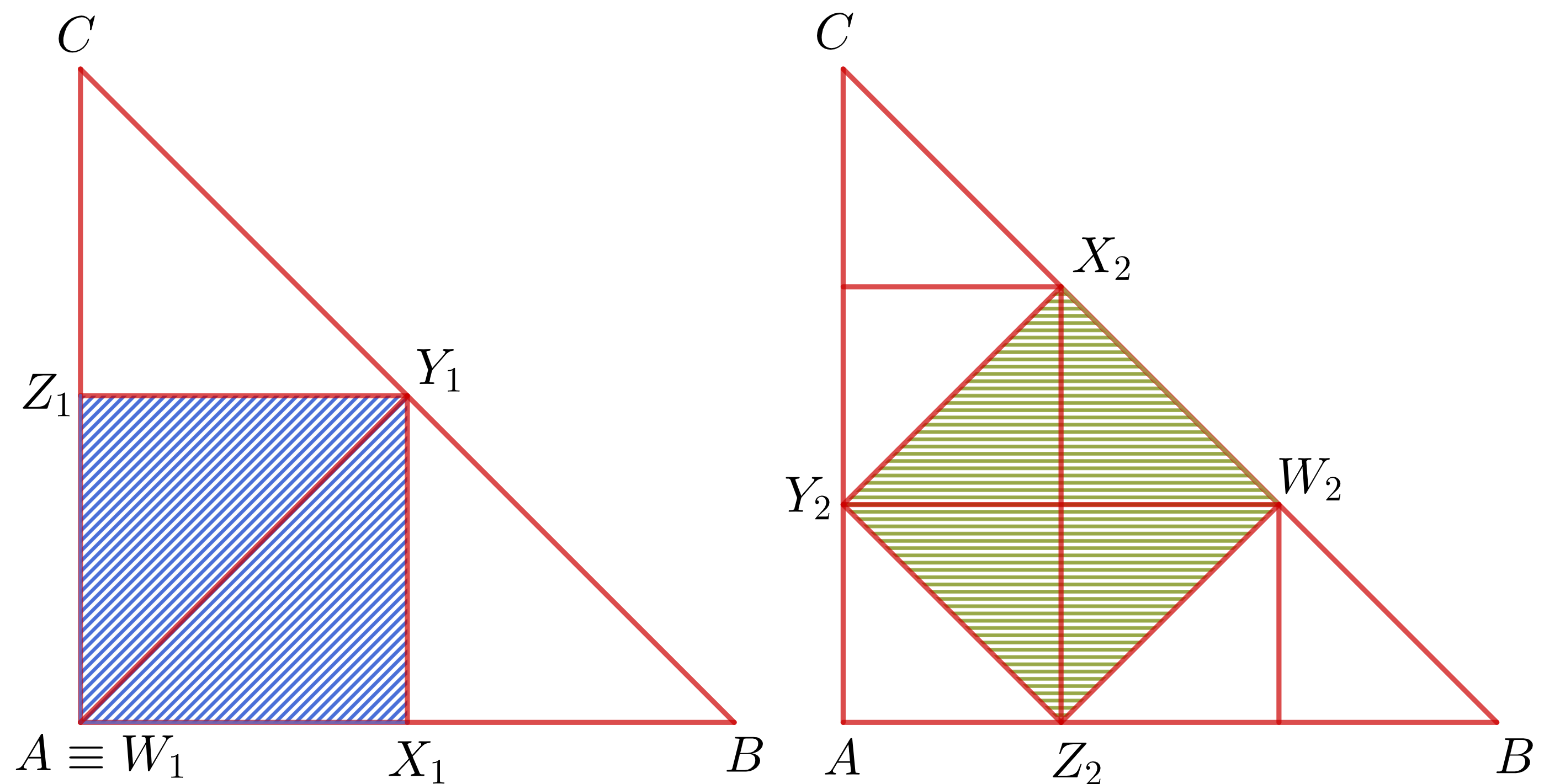
Ešte by som rád spomenul iný postup, ako ukázať, že modrá váza je väčšia. Tento postup použili niektoré z riešení a prišiel mi zaujímavý. Vezmeme si servítku a rozdelíme si ju na menšie trojuholníky ako na obrázku 1. Potom vidíme, že modrá váza tvorí \(\frac24=\frac12\) obsahu servítky a zelená zas \(\frac49\) obsahu servítky. Keďže ale \(\frac12>\frac49\), modrá váza je väčšia.