Zadanie
Po ceste z internátov na univerzitu sa Slovákom (prekvapivo?) podarilo stratiť. Keďže ulice Blagordu sa hemžia nebezpečnými mačkami a psami, chcel sa slovenský tím čo najskôr dostať do bezpečia. Miestny Blagordčan im však dal iba hmlisté inštrukcie. Namiesto priamej cesty ich poslal do päty kolmice na kostolnú cestu a odtiaľ \(18\) krokov doľava a potom \(24\) doprava. Chudáci Slováci museli vyriešiť jednu úlohu ešte pred samotným súťažným dňom, aby sa ho vôbec mohli zúčastniť.
V trojuholníku \(ABC\) označme ako \(D\) pätu výšky na stranu \(AB\). Nech \(M\) je stred strany \(AC\) a \(N\) je stred úsečky \(BD\). Vieme, že \(|AB|=24\) a \(|CD|=18\). Určte \(|MN|\).
V tejto úlohe bolo asi najťažšie začať. Zadané máme dĺžky dvoch úsečiek, ktoré sú na seba kolmé. Avšak máme zistiť dĺžku úsečky, ktorá s nimi na prvý pohľad až tak nesúvisí. Vieme však, že jej krajné body sú stredy nejakých úsečiek. Práve tieto stredy by nás mohli naviesť na použitie stredných priečok.
Dokreslíme si teda stred strany \(BC\), označme ho \(O\). Potom úsečka \(MO\) je stredná priečka v trojuholníku \(ABC\) a úsečka \(NO\) je stredná priečka v trojuholníku \(BDC\). O stredných priečkach je známe, že sú rovnobežné s príslušnou stranou trojuholníka a majú polovičnú dĺžku. Ľahko teda dopočítame, že \(|MO|=12\) a \(|NO|=9\). Navyše, priamky \(AB\) a \(DC\) sú na seba kolmé, a preto sú aj priamky \(MO\) a \(NO\) na seba kolmé. Premyslite si, že to ozaj platí, keď máme zadaný akýkoľvek trojuholník \(ABC\) (špeciálne ak je to tupouhlý trojuholník s tupým uhlom pri vrchole \(A\) alebo \(B\)).
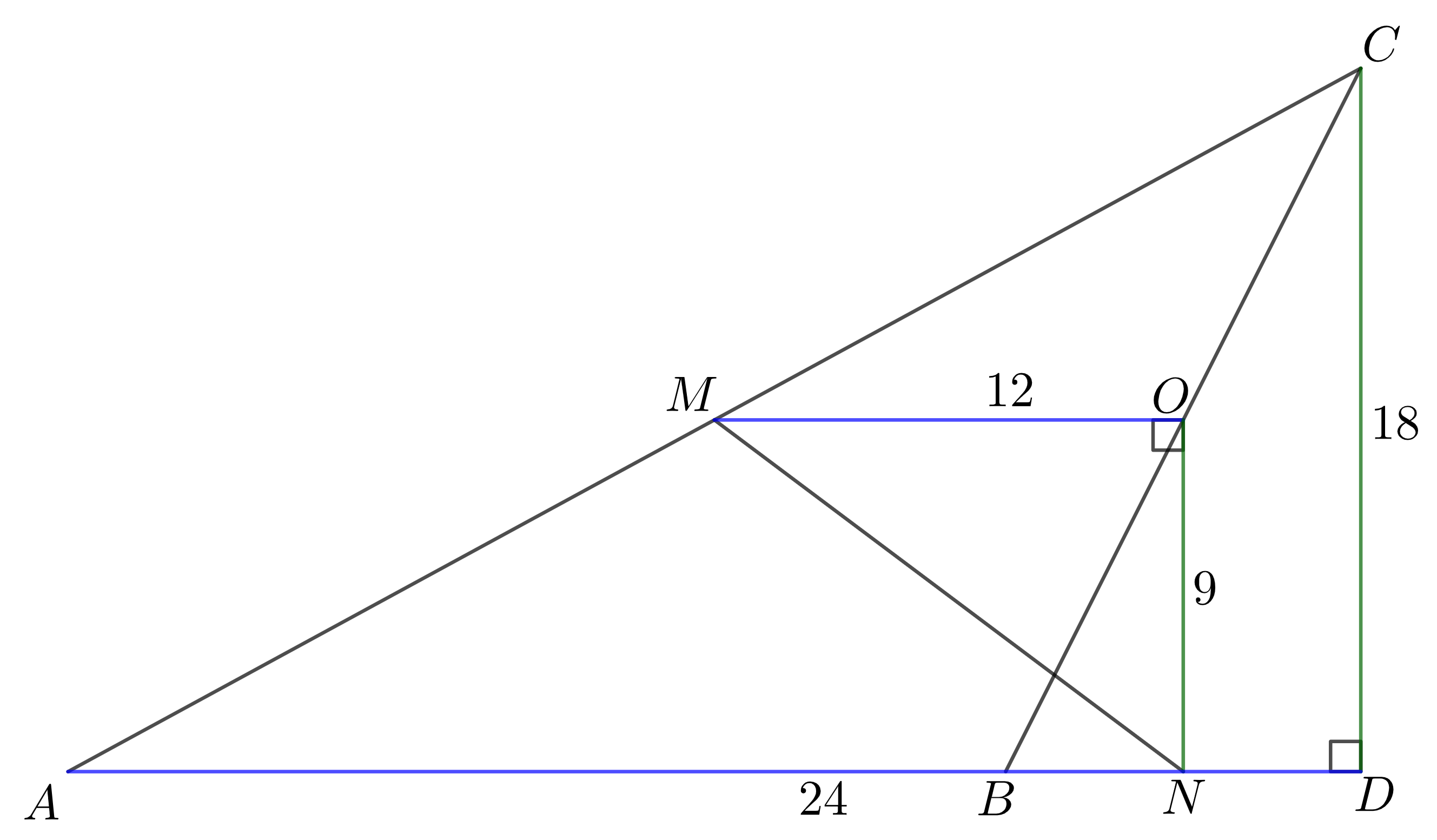
Teraz si už len stačí všimnúť, že trojuholník \(MNO\) je pravouhlý, pričom poznáme dĺžky jeho odvesien. Z Pytagorovej vety potom dostaneme, že strana \(MN\) má dĺžku \(15\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.