Zadanie
Keď sa po prehliadke Bordu Slováci vrátili na internát, rozhodli sa, že si zahrajú spoločenské hry. Vyšli teda na chodbu a sadli si na kružnicu okolo stola. Potom si však všimli, že okolo stola na druhom konci chodby tiež na kružnici sedí nejaká skupinka. Rozhodli sa teda riadiť slovami klasika „Čím viac, team viac“ a kružnice spojili. Majo si všimol, že nech na kružnici sedel kdekoľvek, vždy bolo ich skóre priemerné. Nešlo mu však do hlavy, prečo je to tak.
Kružnice \(k,\, l\) sa pretínajú v bodoch \(P \neq Q\). Na kružnici \(k\) si zvoľme bod \(M\). Priamky \(MP,\, MQ\) pretínajú kružnicu \(l\) postupne v bodoch \(B,\, C\) rôznych od \(P,\, Q\). Označme \(X\) priesečník priamok \(BQ\) a \(CP\). Dokážte, že to, či \(X\) leží na kružnici \(k\), nezávisí od voľby bodu \(M\) (tzn. je to dané iba polohou kružníc \(k,\ l\)). V prípade, že \(X\) leží na kružnici \(k\), dokážte navyše, že \(BC\) je priemerom \(l\).
Predtým, ako začneme úlohu riešiť, sa najprv musíme pozrieť na to, aké rôzne konfigurácie bodov z úlohy môžu nastať, lebo v rôznych konfiguráciach sa môžu odôvodnenia platnosti tvrdení líšiť.
Pre jednoduchosť odkazovania si označme oblúk \(PQ\) kružnice \(k\) ležiaci vnútri kruhu ohraničeného kružnicou \(l\) ako vnútorný oblúk \(PQ_k\) a oblúk \(PQ\) kružnice \(k\) neležiaci vnútri kruhu ohraničeného kružnicou \(l\) ako vonkajší oblúk \(PQ_k\). Podobne si rozdelíme aj oblúk \(PQ\) kružnice \(l\) ako vnútorný oblúk \(PQ_l\) (ležiaci vnútri kruhu ohraničeného kružnicou \(k\)) a ako vonkajší oblúk \(PQ_l\) (neležiaci vnútri kruhu ohraničeného kružnicou \(k\)).
Body \(P\) a \(Q\) sú fixne dané pre každú polohu kružníc \(k\) a \(l\), a teda sa nám stačí zaoberať polohami ostatných bodov. Keďže bod \(M\) ovplyvňuje polohu všetkých ostatných bodov (vynímajúc body \(P,Q\)), tak sa nám stačí pozrieť na prípad, keď \(M\) leží na vnútornom oblúku \(PQ_k\), a na prípad, keď \(M\) leží na vnútornom oblúku \(PQ_k\).
Ak \(M\) leží na vonkajšom oblúku \(PQ_k\), tak môžu nastať tri prípady:
body \(B,C\) ležia obidva na vonkajšom oblúku \(PQ_l\),
body \(B,C\) ležia obidva na vnútornom oblúku \(PQ_l\),
jeden z bodov \(B,C\) leží na vnútornom oblúku \(PQ_l\) a druhý leží na vonkajšom oblúku \(PQ_l\) (pričom je jedno, ktorý z týchto dvoch bodov leží na vnútornom a ktorý na vonkajšom – tieto dve situácie sú symetrické, a teda sa nám stačí zaoberať len jednou z nich).
Iné prípady v tejto možnosti nemôžu nastať, lebo body \(B,C\) sú zo zadania rôzne od bodov \(P,Q\).
Ak \(M\) leží na vnútornom oblúku \(PQ_k\), tak body \(B,C\) musia nutne ležať na vonkajšom oblúku \(PQ_l\). Je to preto, lebo v tomto prípade bod \(M\) leží vnútri kruhu ohraničeného kružnicou \(l\), a teda polpriamka \(MQ\), ktorá vychádza z vnútorného bodu kruhu, pretína kružnicu najviac jedenkrát (a to práve v bode \(Q\)) a polpriamka \(QM\), ktorá vychádza z bodu na kružnici \(l\), leží celá v polrovine určenej priamkou \(PQ\), ktorá obsahuje vonkajší oblúk \(PQ_l\), a teda kružnicu \(l\) nevie preťať v bode ležiacom v druhej polrovine určenej priamkou \(PQ\) (tá polrovina, ktorá obsahuje vnútorný oblúk \(PQ_l\)), a teda musí kružnicu \(l\) preťať na vonkajšom oblúku \(PQ_l\). Podobne je to s priesečníkmi polpriamok \(PM\) a \(MP\) s kružnicou \(l\).
Musíme teda preriešiť \(4\) rôzne prípady polohy bodov \(M,B,C\).
Predtým, než sa pozrieme na jednotlivé prípady, si zavedieme ešte jedno označenie. Pre danú konfiguráciu kružníc \(k,l\) má tetiva \(PQ\) v obidvoch kružniciach fixnú dĺžku. Preto aj obvodové uhly v kružniciach \(k,l\) nad tetivou \(PQ\) budú mať fixnú veľkosť. Pre kružnicu \(k\) a jej vonkajší oblúk \(PQ_k\) si označíme obvodový uhol k tetive \(PQ\) ako \(\alpha\). Podobne pre kružnicu \(l\) a jej vonkajší oblúk \(PQ_l\) si označíme obvodový uhol k tetive \(PQ\) ako \(\beta\).
Teraz sa už môžeme pustiť do rozoberania jednotlivých konfigurácií.
1. konfigurácia - bod \(M\) leží na vonkajšom oblúku \(PQ_k\), body \(B,C\) ležia obidva na vonkajšom oblúku \(PQ_l\)
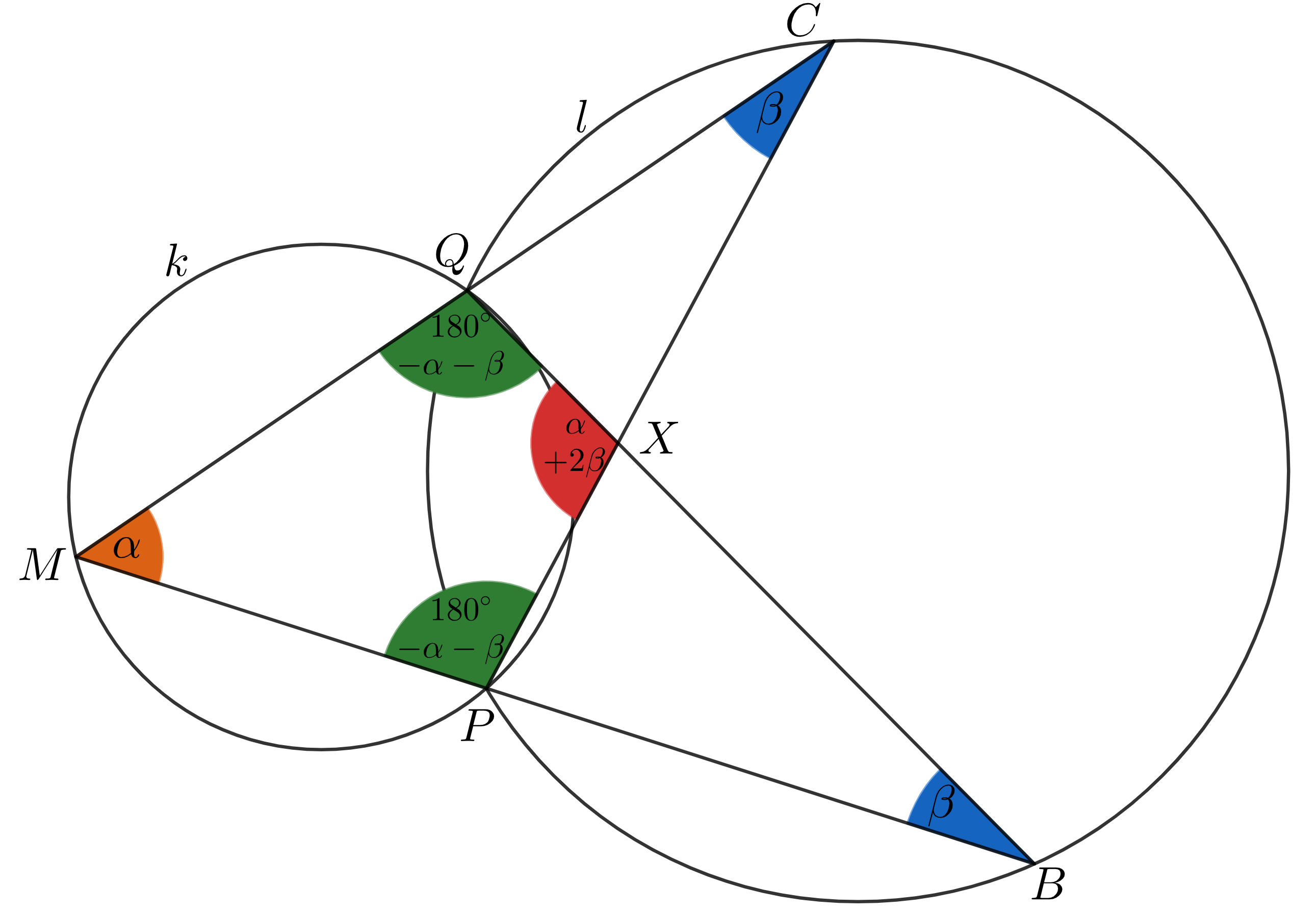
Uhol \(PMQ\) má veľkosť \(\alpha\), lebo je to obvodový uhol nad tetivou \(PQ\) v kružnici \(k\) a bod \(M\) leží na vonkajšom oblúku \(PQ_k\). Ďalej vieme, že \(|\measuredangle PCQ|=|\measuredangle PBQ|=\beta\), lebo je to obvodový uhol nad tetivou \(PQ\) v kružnici \(l\) a body \(B,C\) ležia na vonkajšom oblúku \(PQ_l\). Zo súčtu veľkostí vnútorných uhlov trojuholníka \(MQB\) vieme, že \[|\measuredangle MQB|=180^{\circ}-|\measuredangle QMB|-|\measuredangle QBM|=180^{\circ}-|\measuredangle QMP|-|\measuredangle QBP|=180^{\circ}-\alpha-\beta.\] Podobne zo súčtu veľkostí vnútorných uhlov trojuholníka \(MPC\) vieme, že \[|\measuredangle MPC|=180^{\circ}-|\measuredangle PMC|-|\measuredangle PCM|=180^{\circ}-|\measuredangle PMQ|-|\measuredangle PCQ|=180^{\circ}-\alpha-\beta.\] Zo súčtu vnútorných uhlov v štvoruholníku \(MPXQ\) dostávame, že \[\begin{align} |\measuredangle QXP|&=360^{\circ}-|\measuredangle XQM|-|\measuredangle QMP|-|\measuredangle MPX|=360^{\circ}-|\measuredangle BQM|-|\measuredangle QMP|-|\measuredangle MPC|=\\&=360^{\circ}-(180^{\circ}-\alpha-\beta)-\alpha-(180^{\circ}-\alpha-\beta)=\alpha+2\beta. \end{align}\] Získavame, že \(|\measuredangle QXP|=\alpha+2\beta\), čo je hodnota, ktorá nie je závislá na polohe bodu \(M\), ale len na polohe kružníc \(k,l\). Tým sme dokázali prvú časť zadania pre možnosť túto konfiguráciu.
Predpokladajme teda, že bod \(X\) leží na kružnici \(k\). Potom je štvoruholník \(MPXQ\) tetivový, a teda \(|\measuredangle MQX|+|\measuredangle MPX|=180^{\circ}\). Z toho vyplýva, že: \[\begin{align} 180^{\circ}-\alpha-\beta+180^{\circ}-\alpha-\beta&=180^{\circ},\\ 180^{\circ}&=2\cdot(\alpha+\beta),\\ 90^{\circ}&=\alpha+\beta. \end{align}\] Keďže uhol \(\measuredangle MQX\) je susedný uhol s uhlom \(\measuredangle XQC\), tak dostávame, že platí \(|\measuredangle BQC|=|\measuredangle XQC|=180^{\circ}-(180^{\circ}-\alpha-\beta)=\alpha+\beta=90^\circ\). Uhol \(\measuredangle BQC\) je teda pravý, z čoho vyplýva, že tetiva \(BC\), nad ktorou je tento uhol obvodovým uhlom, je priemer kružnice \(l\). Tým sme dokázali pre túto konfiguráciu aj druhú časť zadania.
2. konfigurácia - bod \(M\) leží na vonkajšom oblúku \(PQ_k\), body \(B,C\) ležia obidva na vnútornom oblúku \(PQ_l\)
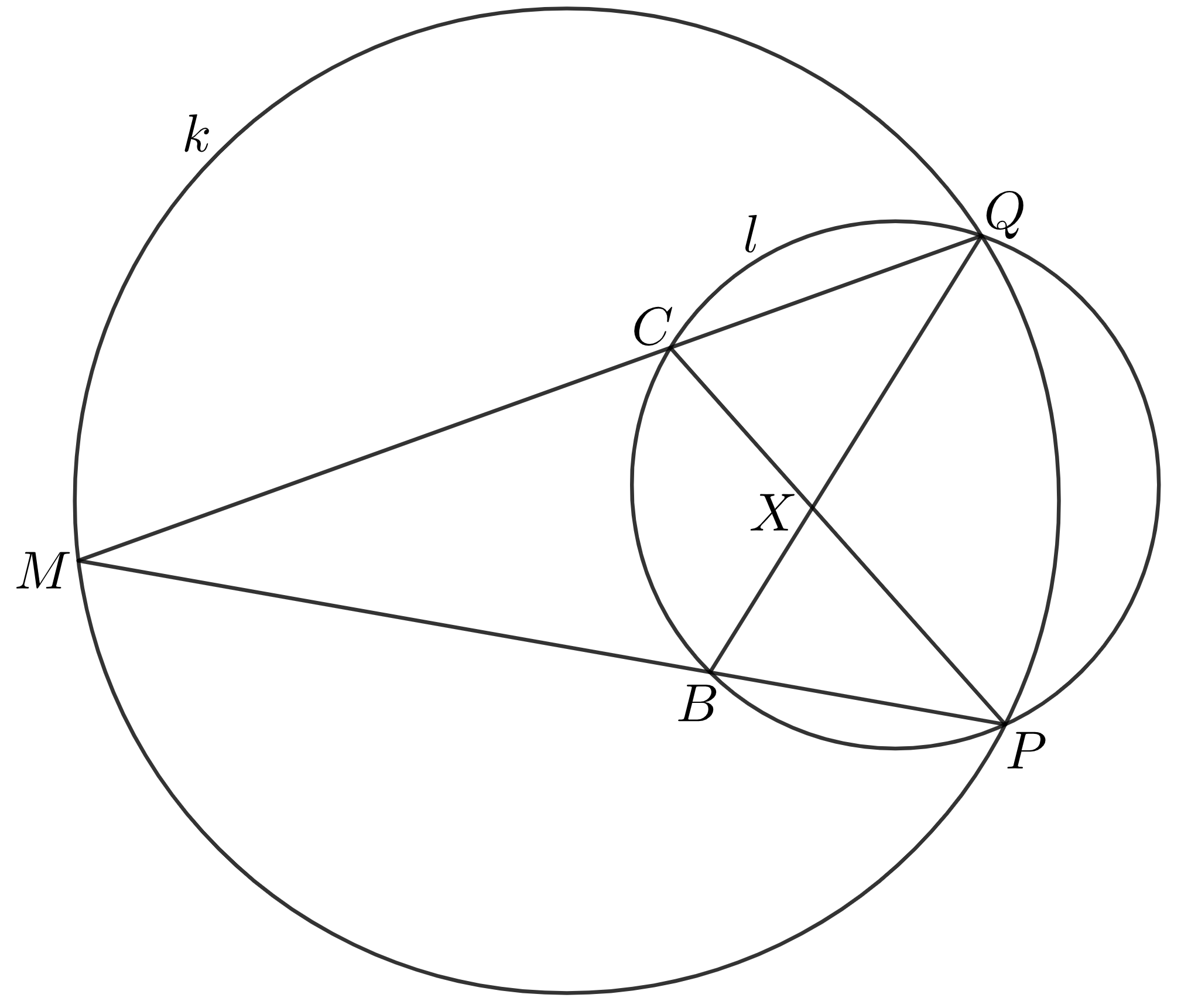
V tomto prípade sa nikdy nemôže stať, že by bod \(X\) ležal na kružnici \(k\). Je to preto, lebo bod \(X\) bude ležať v polrovine určenej priamkou \(QP\), ktorá obsahuje bod \(M\), a teda by bod \(X\) mohol ležať na kružnici \(k\) len vtedy, ak by ležal na vonkajšom oblúku \(PQ_k\). To však nie je možné, keďže poradie bodov \(Q,C,B,P\) na kružnici \(l\) je presne takéto, kvôli tomu, že body \(C,Q\) ležia v jednej polrovine určenej osou uhla \(QMP\) a body \(B,P\) ležia v druhej polrovine určenej touto osou, a zároveň body \(B,C\) ležia na vnútornom oblúku \(PQ_l\). Preto body \(Q,C,B,P\) tvoria štvoruholník v tomto poradí a bod \(X\) leží na priesečníku jeho uhlopriečok. Tento priesečník uhlopriečok musí byť vnútri štvoruholníka, lebo tento štvoruholník je konvexný, a keďže \(X\) leží vnútri tohto štvoruholníka, tak leží aj vnútri kruhu ohraničeného kružnicou \(l\). Tým pádom nevie ležať na vonkajšom oblúku \(PQ_k\), lebo ten bol definovaný ako ten oblúk \(k\), ktorý neleží vnútri kruhu ohraničeného kružnicou \(l\).
3. konfigurácia - bod \(M\) leží na vonkajšom oblúku \(PQ_k\), bod \(B\) leží na vonkajšom oblúku \(PQ_l\) a bod \(C\) leží na vnútornom oblúku \(PQ_l\)
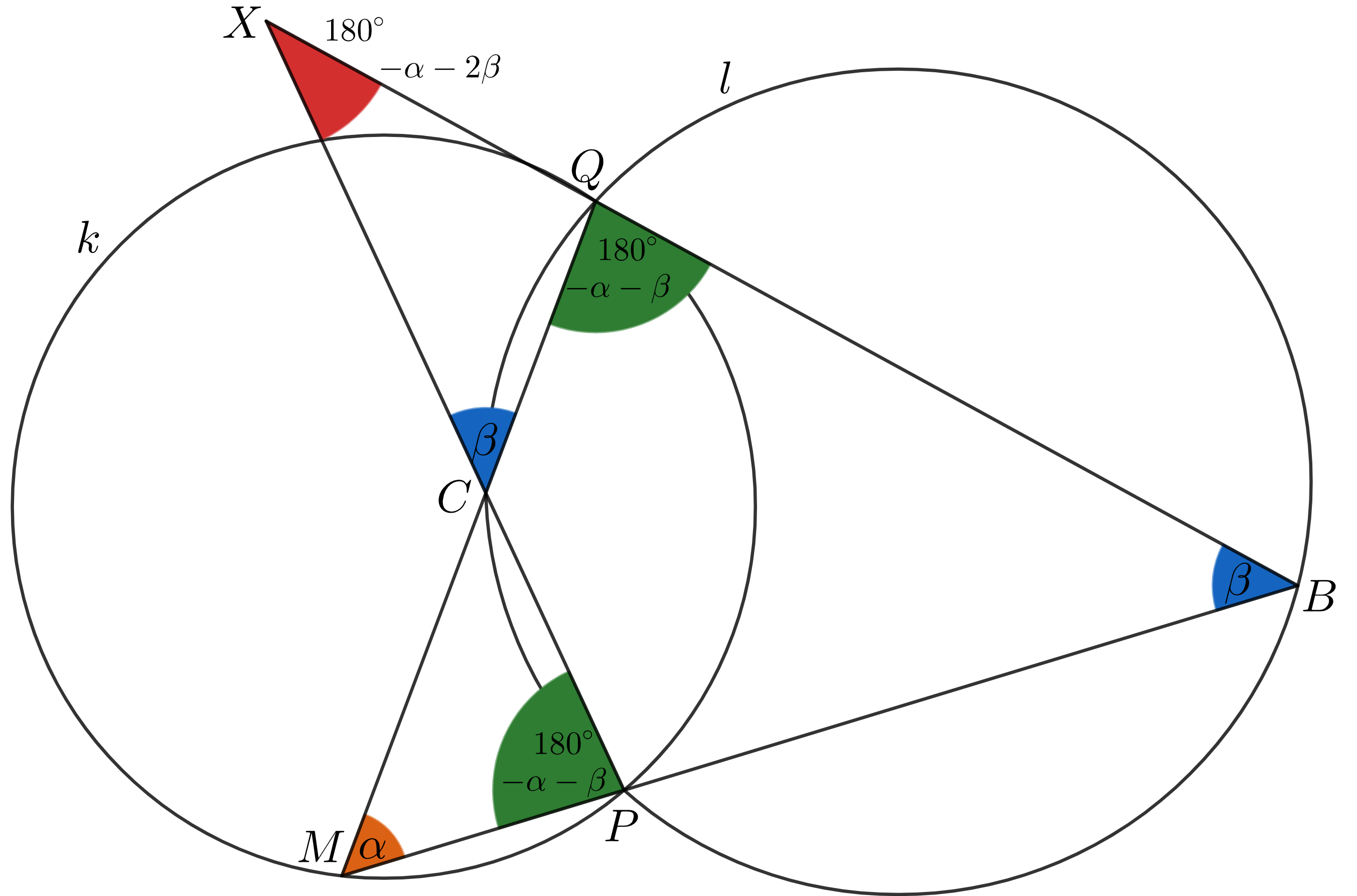
Uhol \(PMQ\) má veľkosť \(\alpha\), lebo je to obvodový uhol nad tetivou \(PQ\) v kružnici \(k\) a bod \(M\) leží na vonkajšom oblúku \(PQ_k\). Ďalej vieme, že \(|\measuredangle PCQ|=180^{\circ}-\beta\) a \(|\measuredangle PBQ|=\beta\), lebo sú to obvodové uhly nad tetivou \(PQ\) v kružnici \(l\), bod \(B\) leží na vonkajšom oblúku \(PQ_l\) a bod \(C\) leží na vnútornom oblúku \(PQ_l\). Zo súčtu veľkostí vnútorných uhlov trojuholníka \(MQB\) vieme, že \[|\measuredangle MQB|=180^{\circ}-|\measuredangle QMB|-|\measuredangle QBM|=180^{\circ}-|\measuredangle QMP|-|\measuredangle QBP|=180^{\circ}-\alpha-\beta.\] Podobne zo súčtu veľkostí vnútorných uhlov trojuholníka \(MPC\) vieme, že \[|\measuredangle MPC|=180^{\circ}-|\measuredangle PMC|-|\measuredangle PCM|=180^{\circ}-|\measuredangle PMQ|-(180^{\circ}-|\measuredangle PCQ|)=180^{\circ}-\alpha-\beta.\] Zo súčtu vnútorných uhlov v trojuholníku \(XCQ\) dostávame, že \[\begin{align} |\measuredangle QXC|&=180^{\circ}-|\measuredangle XQC|-|\measuredangle XCQ|=180^{\circ}-(180^{\circ}-|\measuredangle BQM|)-|\measuredangle PCM|=\\&=180^{\circ}-(180^{\circ}-(180^{\circ}-\alpha-\beta))-\beta)=180^{\circ}-\alpha-2\beta. \end{align}\] Získavame, že \(|\measuredangle QXP|=180^{\circ}-\alpha-2\beta\), čo je hodnota, ktorá nie je závislá na polohe bodu \(M\), ale len na polohe kružníc \(k,l\). Tým sme dokázali prvú časť zadania pre túto konfiguráciu.
Predpokladajme teda, že bod \(X\) leží na kružnici \(k\). Potom je štvoruholník \(MPQX\) tetivový, a teda \(|\measuredangle PMQ|=|\measuredangle PXQ|\), lebo sú to obvodové uhly nad jednou tetivou. Z toho vyplýva, že: \[\begin{align} \alpha&=180^{\circ}-\alpha-2\beta,\\ 2\cdot(\alpha+\beta)&=180^{\circ},\\ \alpha+\beta&=90^{\circ}. \end{align}\] Keďže uhol \(\measuredangle MQX\) je susedný uhol s uhlom \(\measuredangle MQB\), tak dostávame, že platí \(|\measuredangle BQM|=|\measuredangle BQC|=180^{\circ}-\alpha-\beta=90^{\circ}\). A teda je uhol \(\measuredangle BQC\) pravý, z čoho vyplýva, že tetiva \(BC\), nad ktorou je tento uhol obvodovým uhlom, je priemer kružnice \(l\). Tým sme dokázali pre túto konfiguráciu aj druhú časť zadania.
4. konfigurácia - bod \(M\) leží na vnútornom oblúku \(PQ_k\), body \(B,C\) ležia obidva na vonkajšom oblúku \(PQ_l\)
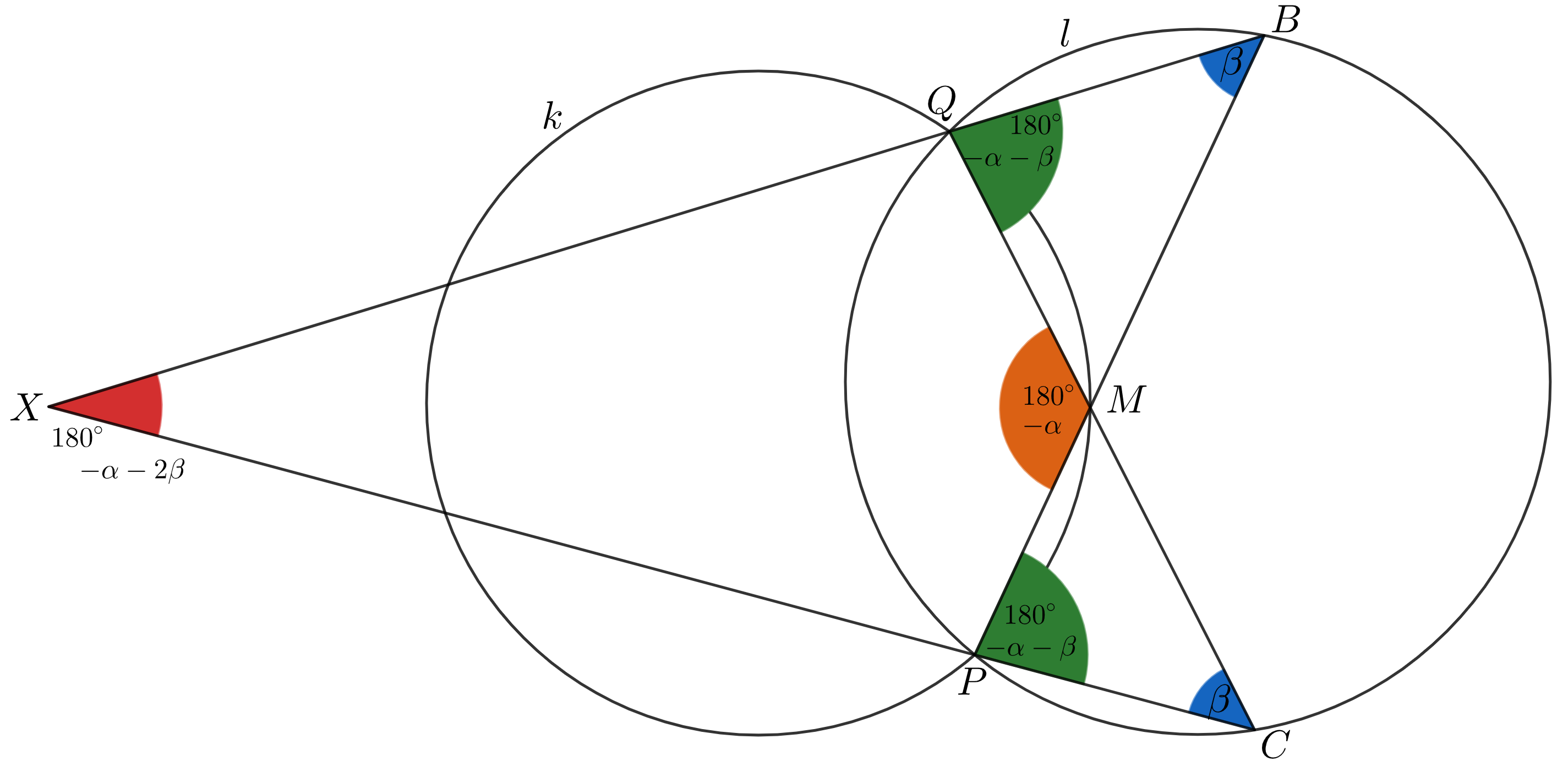
Uhol \(PMQ\) má veľkosť \(180^{\circ}-\alpha\), lebo je to obvodový uhol nad tetivou \(PQ\) v kružnici \(k\) a bod \(M\) leží na vnútornom oblúku \(PQ_k\). Ďalej vieme, že \(|\measuredangle PCQ|=|\measuredangle PBQ|=\beta\), lebo je to obvodový uhol nad tetivou \(PQ\) v kružnici \(l\) a body \(B,C\) ležia na vonkajšom oblúku \(PQ_l\). Zo súčtu veľkostí vnútorných uhlov trojuholníka \(MQB\) vieme, že \[|\measuredangle MQB|=180^{\circ}-|\measuredangle QMB|-|\measuredangle QBM|=180^{\circ}-|\measuredangle QMP|-|\measuredangle QBP|=180^{\circ}-\alpha-\beta.\] Podobne zo súčtu veľkostí vnútorných uhlov trojuholníka \(MPC\) vieme, že \[|\measuredangle MPC|=180^{\circ}-|\measuredangle PMC|-|\measuredangle PCM|=180^{\circ}-|\measuredangle PMQ|-|\measuredangle PCQ|=180^{\circ}-\alpha-\beta.\] Zo súčtu vnútorných uhlov v štvoruholníku \(MPXQ\) dostávame, že \[\begin{align} |\measuredangle QXP|&=360^{\circ}-|\measuredangle XQM|-|\measuredangle QMP|-|\measuredangle MPX|=360^{\circ}-(180^{\circ}-|\measuredangle BQM|)-|\measuredangle QMP|-(180^{\circ}-|\measuredangle MPC|)=\\&=360^{\circ}-(\alpha+\beta)-(180^{\circ}-\alpha)-(\alpha+\beta)=180^{\circ}-\alpha-2\beta. \end{align}\] Získavame, že \(|\measuredangle QXP|=180^{\circ}-\alpha-2\beta\), čo je hodnota, ktorá nie je závislá na polohe bodu \(M\), ale len na polohe kružníc \(k,l\). Tým sme aj pre túto konfiguráciu dokázali prvú časť zadania.
Predpokladajme teda, že bod \(X\) leží na kružnici \(k\). Potom je štvoruholník \(MPXQ\) tetivový, a teda \(|\measuredangle MQX|+|\measuredangle MPX|=180^{\circ}\). Z toho vyplýva, že: \[\begin{align} \alpha+\beta+\alpha+\beta&=180^{\circ},\\ 2\cdot(\alpha+\beta)&=180^{\circ},\\ \alpha+\beta&=90^{\circ}. \end{align}\] Keďže uhol \(\measuredangle MQX\) je susedný uhol s uhlom \(\measuredangle MQB\), tak dostávame, že platí \(|\measuredangle MQB|=|\measuredangle BQC|=180^{\circ}-(\alpha+\beta)=180^{\circ}-\alpha-\beta\). A teda je uhol \(\measuredangle BQC\) pravý, z čoho vyplýva, že tetiva \(BC\), nad ktorou je tento uhol obvodovým uhlom, je priemer kružnice \(l\). Tým sme dokázali pre túto konfiguráciu aj druhú časť zadania.
Vyššie sme pre všetky konfigurácie dokázali vlastnosti zo zadania, a teda sme vyriešili celú úlohu.
Alternatívne sa dala úloha riešiť za pomoci orientovaných uhlov, čo by nám umožnilo vyhnúť sa rozpisovaniu všetkých konfigurácií.
Poznámka
Viacerí z vás ste si správne všimli, že priamky \(QB\) a \(PC\) môžu byť v posledných dvoch konfiguráciách (pre \(\alpha+2\beta=180^\circ\)) rovnobežné, a teda nám nevzniká bod \(X\). V zadaní sme však zabudli napísať, že týmto okrajovým prípadom sa nemáte venovať, keďže v nich skúmané tvrdenie vlastne vôbec nedávalo zmysel. Za chybu sa ospravedlňujeme.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.