Zadanie
Kaju už ale nudí stáť na mieste. Začala teda tlačiť všetkých vedúcich smerom vybratým Marekovou vysnívanou kockou.
Kaja tlačila vedúcich po kružnici \(k\) s priemerom \(AB\). Ďalej je na \(k\) daná tetiva \(PQ\) so stredom \(R\). Nech \(S\), \(T\) sú päty kolmíc na \(AB\) postupne z \(P\), \(Q\). Predpokladajme, že body \(R\), \(S\), \(T\) sú rôzne a neležia na jednej priamke. Dokážte, že trojuholník \(RST\) je rovnostranný práve vtedy, keď \(2\cdot |PQ| = |AB|\).
Najprv si nakreslíme obrázok podľa zadania. Mimo bodov, ktoré máme dané, si vyznačíme aj priesečník priamok \(AB\) a \(PQ\), ktorý nazveme \(F\). Prípad keď \(AB \parallel PQ\), a teda bod \(F\) nevznikne, to poriešime nakoniec. Teraz sa pozrieme na obrázok a príde nám taký asymetrický.
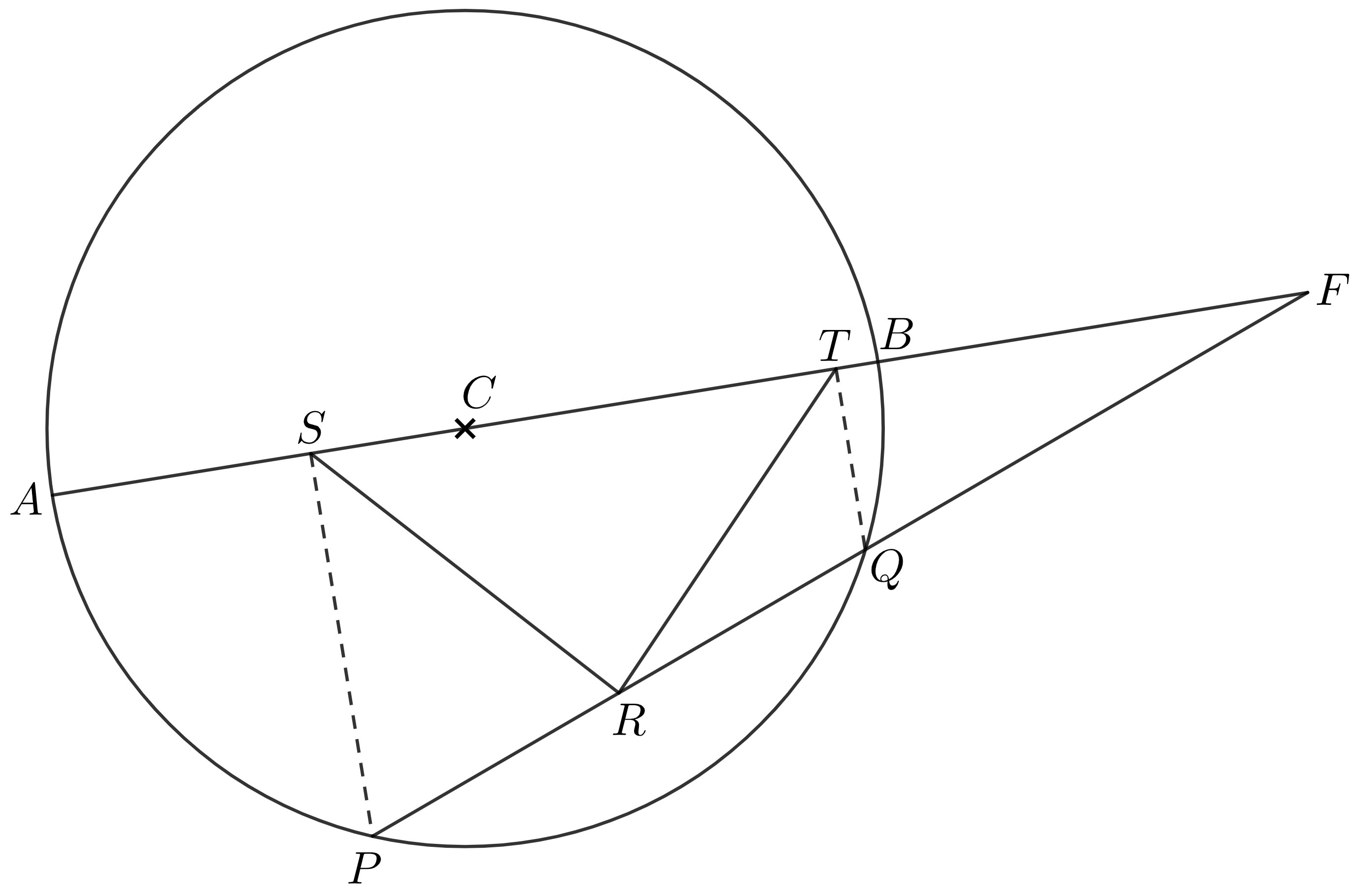
Priestor má dve polroviny a my využívame iba jednu. Tak si povieme, že aj v tej druhej by sa hodilo niečo mať a celú úlohu zosymetríme podľa priamky \(AB\). Možno to ešte neviete, no práve sme vyhrali.
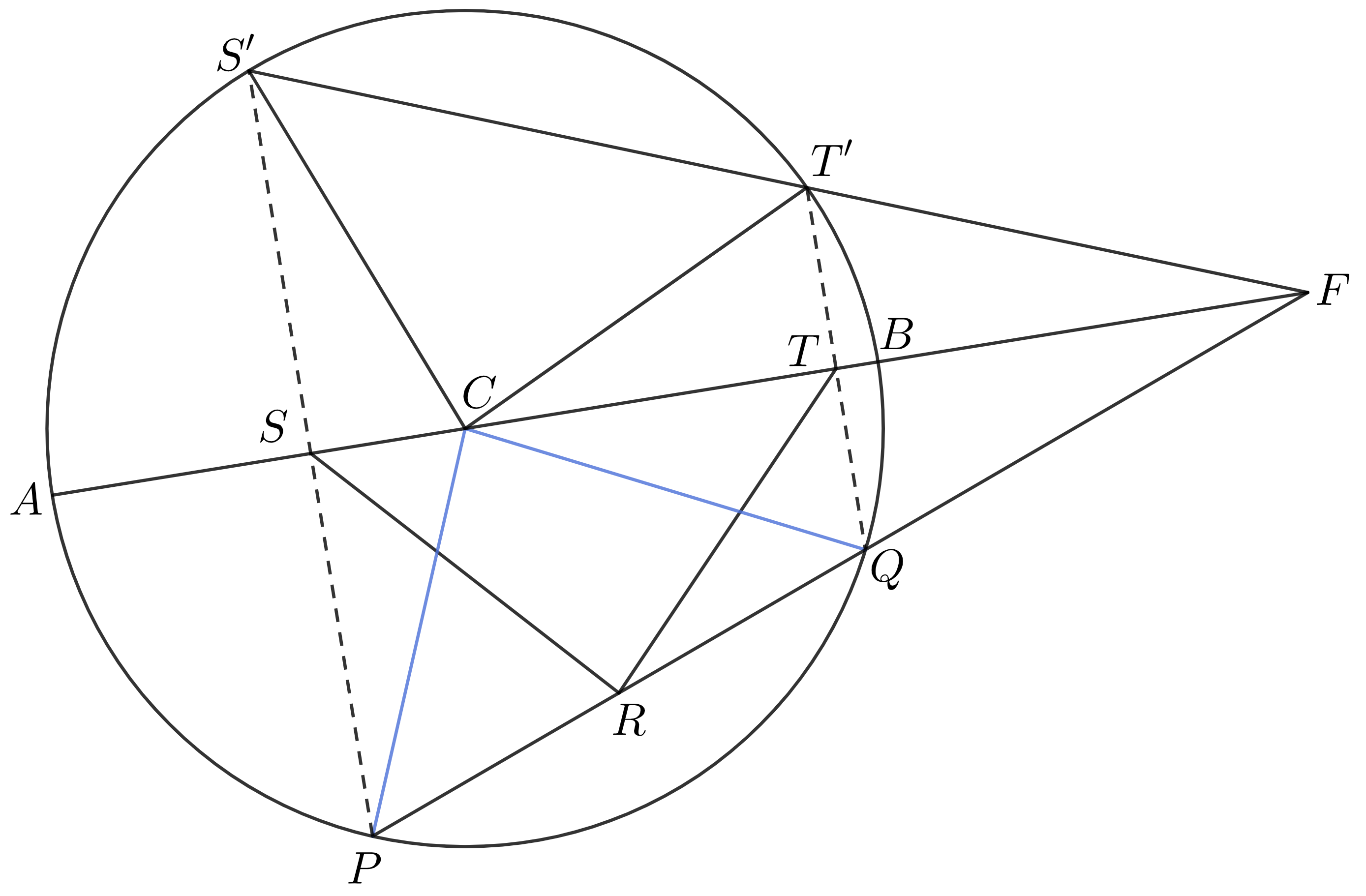
Ak by sa nám podarilo ukázať, že \(\triangle PCQ \sim \triangle SRT\), tak máme hotovo. Prečo? Úsečky \(CP\) a \(CQ\) sú polomermi kružnice \(k\). \(\triangle PCQ\) tak bude rovnostranný práve vtedy, keď \(\lvert PQ \rvert = \frac{\lvert AB \rvert}{2}=r\), takže práve vtedy, keď chceme, aby bol rovnostranný aj \(\triangle SRT\). Poďme teda ukázať ich podobnosť. Najprv \(\triangle PCQ\) a \(\triangle S'CT'\), sú podobné, lebo sú iba obrazmi v osovej symetrii. Stačí nám teda, aby \(\triangle S'CT' \sim \triangle SRT\).
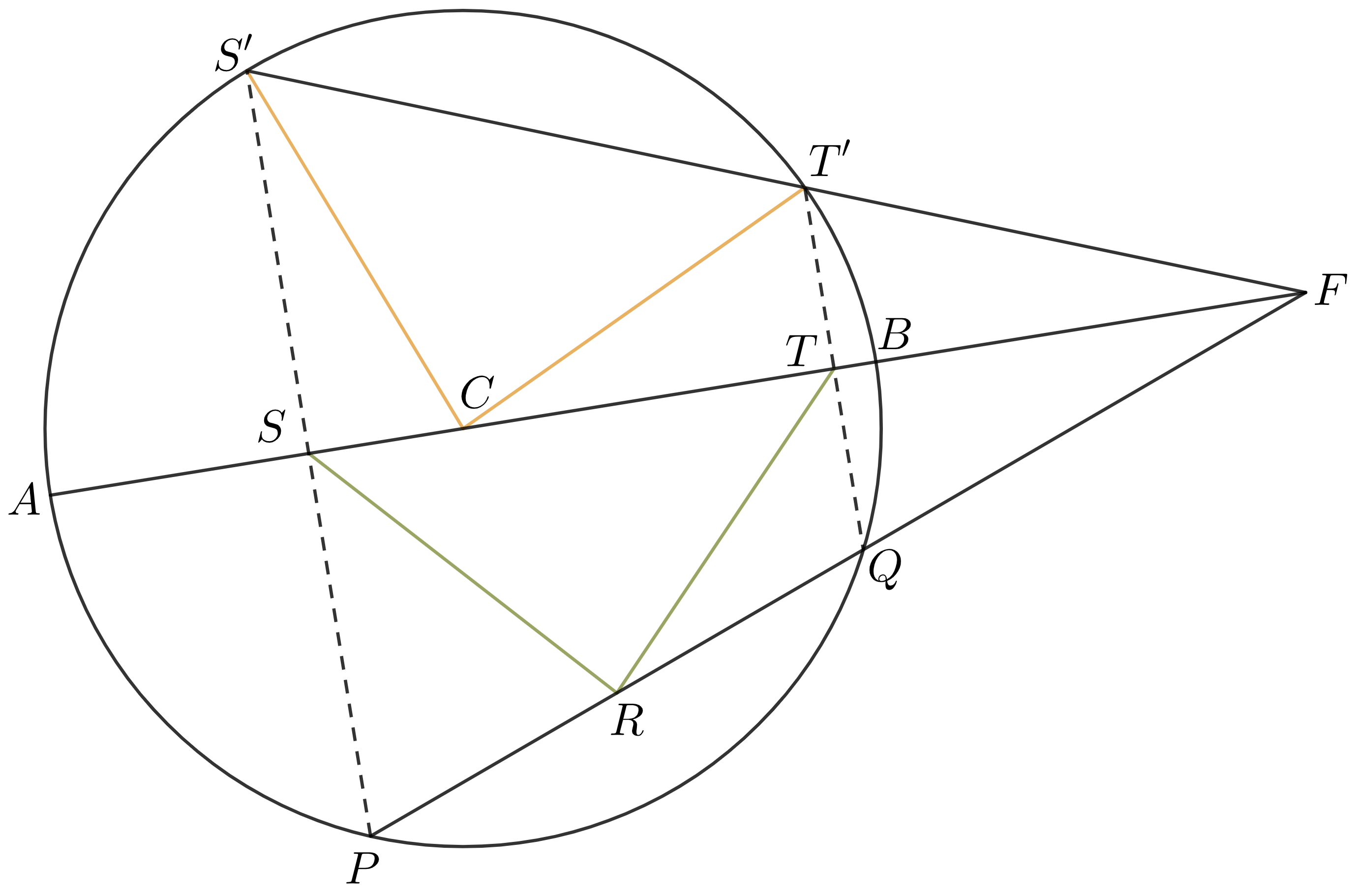
Tu sa nám začína črtať špirálna podobnosť so stredom v \(F\) (tak sa tomu vznešene hovorí). Všimnime si, že uhol \(\lvert\angle AFS'\rvert = \lvert\angle PFS\rvert\), znovu ide len o osovú symetriu. Potom, keď otočíme uhol \(\angle AFS'\), na \(\angle PFA\), tak body \(S'\) a \(T'\) nám pristanú na priamke \(AB\) a bod \(C\) na priamke \(PQ\). Nakoniec ešte nájdime koeficient podobnosti pri ktorom sa \(T'\) zobrazí na \(T\). To je iba \(k=\frac{\lvert TF\rvert}{\lvert T'F\rvert}\). Vieme, že \(\triangle SFS' \sim \triangle TFT'\) podľa vety uu. Totiž, zdieľajú uhol pri bode \(F\) a ďalej uhly pri vrcholoch \(S\), \(T\) sú očividne pravé. Potom máme z pomerov dĺžok \(\frac{\lvert SF\rvert}{\lvert S'F\rvert}=\frac{\lvert TF\rvert}{\lvert T'F\rvert} = k\). To ale znamená, že špirálnou podobnosťou s otočením o uhol \(\sphericalangle AFS'\) a koeficientom podobnosti \(k\) sa nám aj \(S'\) zobrazí na \(S\).
Ďalej si uvedomme, že \(\triangle SRT\) je rovnoramenný. Totiž, Keďže \(R\) je stredom \(PQ\), os strany \(ST\) je zároveň aj strednou priečkou lichobežníka \(PQTS\) obsahujúcou bod \(R\), a teda \(R\) leží na osi úsečky \(ST\).
Nakoniec by nás mohlo zaujímať, či sa \(C\) zobrazí na \(R\), no to tak určite bude, keďže oba trojuholníky sú rovnoramenné so základňou \(S'T'\), resp. \(ST\) a posledným vrcholom na priamke \(ST\), resp. \(PQ\), čo sú ramená uhla otočenia.
Práve sa nám podarilo ukázať, že \(\triangle PCQ \sim \triangle SRT\), avšak \(\triangle PCQ\) je rovnostranný práve vtedy keď tetiva \(PQ\), má dĺžku \(\frac{\lvert AB \rvert}{2}=r\).
Ostáva nám ešte poriešiť prípad, keď \(AB \parallel PQ\). Vtedy sú však \(\triangle PCQ\) a \(\triangle SRT\) dokonca zhodné, lebo \(\lvert RT \rvert = \lvert CQ \rvert\) vyplýva z toho, že ide o uhlopriečky obdĺžnika \(RQTC\). Podobne dostávame aj \(\lvert SR \rvert = \lvert PC \rvert\) a \(\lvert ST \rvert = \lvert PQ \rvert\), keďže v tomto prípade je \(PQTS\) obdĺžnikom, a teda záver ostáva v platnosti.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.