Zadanie
Kráľ bol veľmi múdry a rád sa zaoberal matematikou. Jedného dňa si vzal mapu svojho kráľovstva a začal na nej skúmať rôzne tvary. Zaujali ho najmä štvorce a kružnice. Keď sa pozrel na mapu bližšie, zistil, že niektoré štvorce sú obklopené kružnicami. A tak sa rozhodol, že skúsi zistiť, či je možné, aby stredy kružníc ležali vo vrcholoch nejakého štvorca.
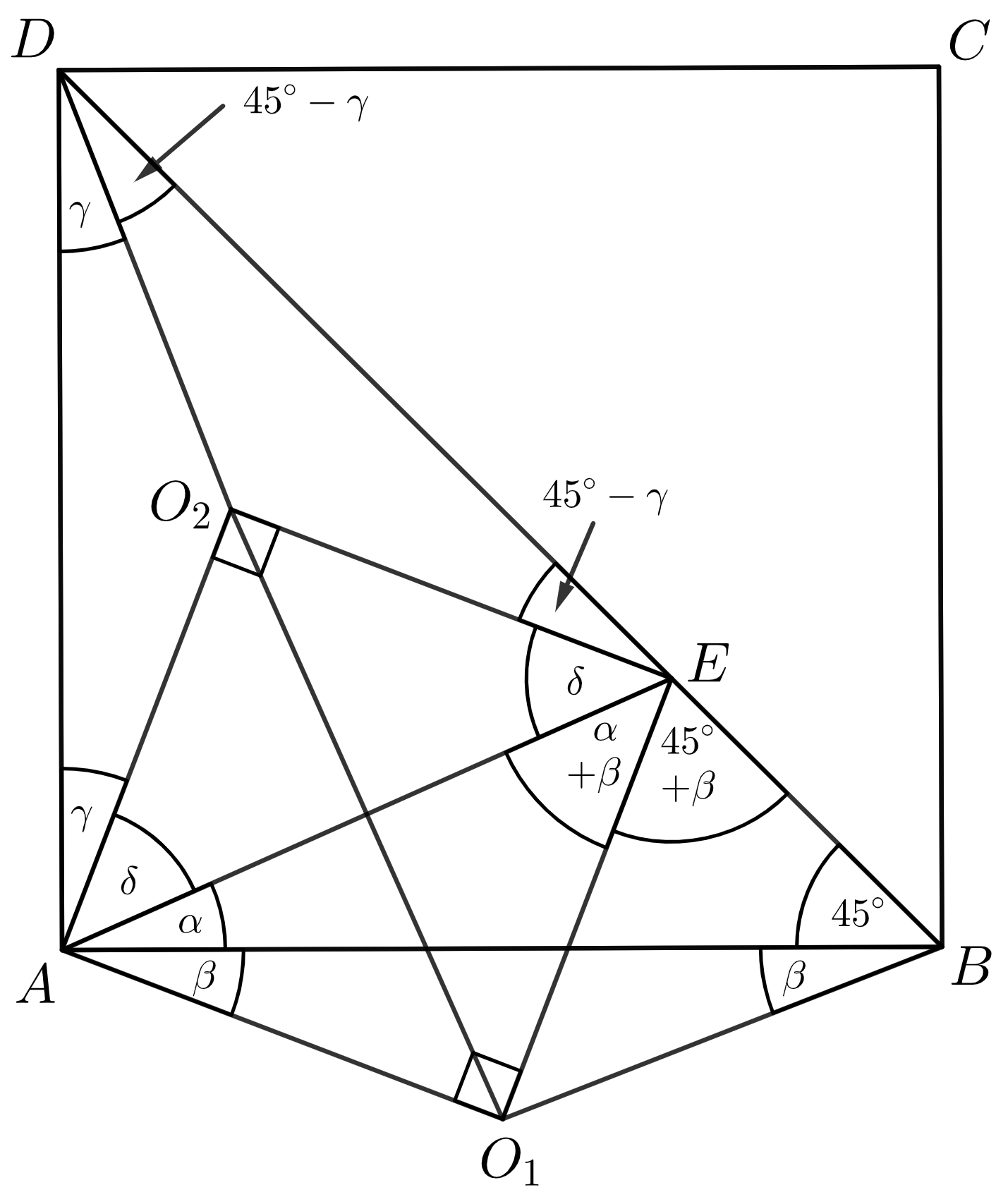
Majme štvorec \(ABCD\) a bod \(E\), ktorý leží vnútri uhlopriečky \(BD\). Nech \(O_1\) je stred kružnice, ktorá prechádza cez body \(A\), \(B\), \(E\), a nech \(O_2\) je stred kružnice, ktorá prechádza cez body \(A\), \(D\), \(E\). Dokážte, že \(AO_1EO_2\) je štvorec.
Označme \(|\sphericalangle BAE|\) ako \(\alpha\) a \(|\sphericalangle BAO_1|\) ako \(\beta\). Keďže \(O_1\) je stred kružnice opísanej trojuholníku \(ABE\), tak \(|AO_1|=|BO_1|\), preto trojuholník \(ABO_1\) je rovnoramenný a \(|\sphericalangle ABO_1|=|\sphericalangle BAO_1|=\beta\). Podobne aj \(|AO_1|=|EO_1|\), čiže \(AO_1E\) je rovnoramenný, a teda \(|\sphericalangle AEO_1|=|\sphericalangle EAO_1|=|\sphericalangle EAB|+|\sphericalangle BAO_1|=\alpha+\beta\). Keďže \(BD\) je uhlopriečka štvorca, tak \(|\sphericalangle ABD|=45^\circ\). Potom ale z toho, že \(|BO_1|=|EO_1|\) (opäť z kružnice opísanej \(ABE\)) máme, že trojuholník \(BEO_1\) je rovnoramenný, z čoho \(|\sphericalangle BEO_1|=|\sphericalangle EBO_1|=|\sphericalangle EBA|+|\sphericalangle ABO_1|=45^\circ+\beta\).
Pozrime sa ďalej na súčet uhlov v trojuholníku \(ABE\). Platí \(180^\circ=|\sphericalangle ABE|+|\sphericalangle BEA|+|\sphericalangle EAB|=45^\circ+(45^\circ+\alpha+2\beta)+\alpha=90^\circ+2(\alpha+\beta)\). Potom ale \(2(\alpha+\beta)=90^\circ\), a preto \(\alpha+\beta=45^\circ\). Všimnime si, že trojuholník \(AEO_1\) je rovnoramenný s uhlami \(45^\circ\) pri základni, a teda oproti nej má uhol \(|\sphericalangle AO_1E|=180^\circ-2\cdot45^\circ=90^\circ\).
Teraz postupujme podobne pre druhú stranu: Označme si \(|\sphericalangle DAO_2|\) ako \(\gamma\) a \(|\sphericalangle EAO_2|\) ako \(\delta\). Potom z rovnoramenného \(DAO_2\) vieme, že \(|\sphericalangle O_2DA|=|\sphericalangle DAO_2|=\gamma\). Vieme, že \(|\sphericalangle EDA|=45^\circ\) z vlastností uhlopriečok štvorca. Teda \(|\sphericalangle EDO_2|=|\sphericalangle EDA|-|\sphericalangle O_2DA|=45^\circ-\gamma\). Z rovnoramennosti trojuholníka \(EDO_2\) vieme, že \(|\sphericalangle EDO_2|=|\sphericalangle O_2ED|=45^\circ-\gamma\). Nakoniec sa pozrieme na rovnoramenný trojuholník \(AEO_2\). Vieme, že \(|\sphericalangle O_2AE|=\delta\), a z toho aj \(|\sphericalangle AEO_2|=|\sphericalangle O_2AE|=\delta\).
Už poznáme všetky uhly na to, aby sme zistili čo potrebujeme. Zo súčtu uhlov v trojuholníku \(AED\) vidíme, že \(180^\circ=2\gamma+2\cdot(45^\circ-\gamma)+2\delta=90^\circ+2\delta\), z čoho vidíme, že \(\delta=45^\circ\), a \(|\sphericalangle AEO_2|=|\sphericalangle O_2AE|=\delta=45^\circ\). Opäť si všimnime, že trojuholník \(AEO_2\) je rovnoramenný s uhlami \(45^\circ\) pri základni, a teda oproti nej má uhol veľkosti \(|\sphericalangle EO_2A|=180^\circ-2\cdot45^\circ=90^\circ\).
Práve sme celkom pracne pre konkrétny uhol \(45^\circ\) dokázali, že veľkosť uhla, ktorý zviera tetiva so stredom, je dvojnásobkom uhla, ktorý zviera s ľubovoľným bodom na „správnej“ strane kružnice. Toto je v geometrických úlohách pomerne často používaná vlastnosť nazývaná aj veta o obvodovom a stredovom uhle. Ak ste o nej ešte nepočuli, odporúčame si niečo o tom prečítať (napríklad v Zbierke úloh KMS1, Kapitola 2, sekcia 1) a potom sa zamyslieť, ako veľmi by to zjednodušilo toto riešenie.
Teda sme zistili, že trojuholníky \(O_1EA\) a \(O_2AE\) sú pravouhlé a rovnoramenné. Ďalej, pre veľkosti uhlov \(\sphericalangle EAO_1\), \(\sphericalangle O_1EA\), \(\sphericalangle AEO_2\) a \(\sphericalangle O_2AE\) platí \(|\sphericalangle EAO_1|=|\sphericalangle O_1EA|=|\sphericalangle AEO_2|=|\sphericalangle O_2AE|=45^\circ\), z čoho dostávame \(|\sphericalangle AO_1E|=|\sphericalangle O_1EO_2|=|\sphericalangle EO_2A|=|\sphericalangle O_2AO_1|=90^\circ\). Teda útvar \(AO_1EO_2\) je obdĺžnik. No keďže z rovnoramennosti napr. trojuholníka \(AO_1E\) sú dve susedné strany útvaru \(AO_1EO_2\) rovnakej veľkosti, jedná sa o štvorec.
Zamyslime sa ešte, čo by sa stalo, keby situácia vyzerala inak ako na našom nákrese. Všimnime si, že uhly v trojuholníku \(ADE\) a uhly v trojuholníku \(ABE\) sme spočítali „nezávisle“. To znamená, že \(45^\circ\) a \(90^\circ\) uhly nám vyjdú na správnych miestach aj vtedy, keď je stred kružnice opísanej mimo štvorca, aj vtedy, keď je stred kružnice opísanej v štvorci. A čo keby bol ten stred na hrane štvorca? Jednoducho by sme mali \(\beta=0^\circ\) (resp. \(\gamma=0^\circ\)) a celý dôkaz by prebehol tiež.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.