9. Keď Matematika Sedí vzorové riešenie

Začnime dôkladným pohľadom na to, čo máme dokázať. Trojuholník \(ABC\) je rovnoramenný, čo znamená, že os \(\sphericalangle BAC\) je zároveň výškou na \(BC\), ťažnicou z vrcholu \(A\), a osou strany \(BC\). Zvlášť ten posledný fakt sa nám môže zísť. Stačí nám totiž ukázať, že \(BCT\) je rovnoramenný trojuholník so základňou \(BC\). V skutočnosti by nás k cieľu doviedol aj dôkaz, že \(T\) leží na niektorej zo zvyšných priamok. Keď nevieme, kam nás naše riešenie zavedie, je fajn mať na mysli aj ostatné možnosti.

Druhá vec, na ktorú si treba dať pozor, sú rôzne konfigurácie nášho obrázka. Môžeme si všimnúť, že ak \(|BX| > |XC|\), tak priamka \(BT\) bude viesť mimo trojuholníka a bod \(T\) nutne vznikne mimo. V prípade \(|BX| = |CX|\) je \(BT\) totožná s \(BC\). Poslednou možnosťou je \(|BX| < |XC|\), kedy bude \(T\) vnútri trojuholníka. Poďme však pekne postupne.

Bod \(X\) je bližšie k \(C\)

Podľa zadania \(|\sphericalangle BXY| = |\sphericalangle CXZ|\). Tento uhol označíme \(\delta\). Vďaka rovnoramennosti \(ABC\) vidíme tiež, že \(|\sphericalangle YBX| = |\sphericalangle ZCX|\). Trojuholníky \(XBY\) a \(XCZ\) sú teda podobné podľa vety \(uu\).

Uhol \(\delta\) sa nachádza aj „z druhej strany“ úsečky \(BC\). Označme \(E\) priesečník priamok \(XY\) a \(BT\). Máme tam uhly vrcholové k \(\sphericalangle BXY\) a \(\sphericalangle CXZ\), menovite \(\sphericalangle CXE\) a \(\sphericalangle BXT\). My sa však pozrieme na ich doplnky do \(180°\). Platí \[|\sphericalangle BXE| = 180° - \delta = |\sphericalangle CXT|.\]

Prečo sú tieto uhly zaujímavé? Lebo ležia v trojuholníkoch \(BXE\) a \(CXT\). Ako sme si povedali už na začiatku, zaujíma nás, či je trojuholník \(BCT\) rovnoramenný, teda, či \(|\sphericalangle XBT| = |\sphericalangle XCT|\). Ak to platilo, boli by spomínané trojuholníky \(BXE\) a \(CXT\) podobné. To zatiaľ nevieme, ale vytýčili sme si o niečo jasnejší cieľ.

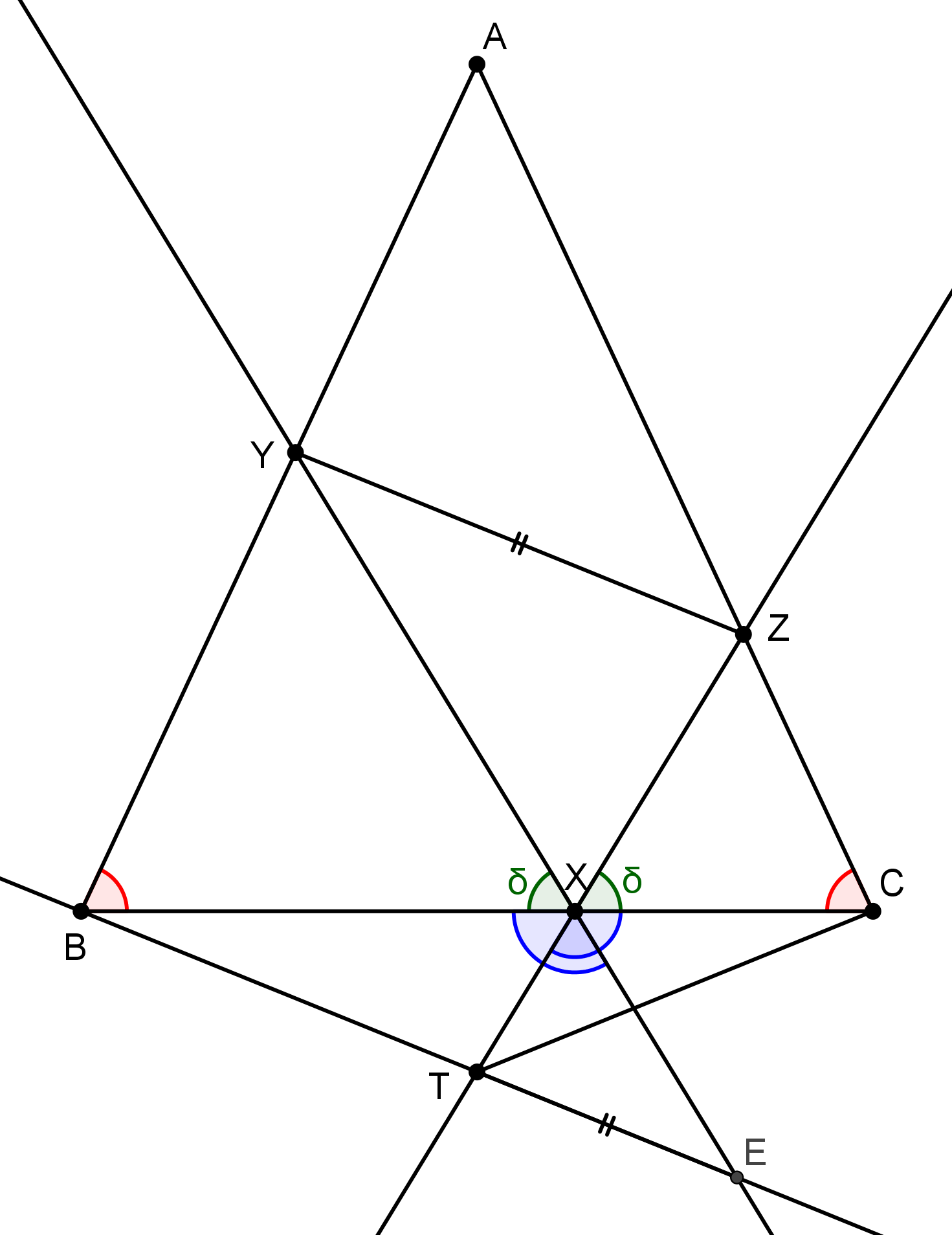
My však chceme použiť podobnosť na to, aby sme ukázali, že nejaké uhly sú rovnaké. Samotnú podobnosť teda musíme skúsiť ukázať inak. Veľa možností nemáme, potrebujeme sa vrhnúť na pomery strán. Vďaka podobnosti \(XBY\) a \(XCZ\) už niečo vieme o stranách \(BX\) a \(CX\), no nevieme, čo sa deje vo zvyšku.

Ešte sme však nevyužili rovnobežky zo zadania. Vďaka rovnobežnosti \(YZ\) a \(BT\) si môžeme všimnúť, že trojuholníky \(XZY\) a \(XTE\) sú rovnoľahlé, a teda podobné. To nám niečo hovorí o úsečkách \(XT\) a \(XE\), ktoré sú súčasťou trojuholníkov, ktorých podobnosť chceme ukázať.

Konkrétne dostávame, pre pomery strán vnútri trojuholníkov, \(|XT|:|XE| = |XZ|:|XY|\). Tu sa nám zíde prvá dokázaná podobnosť – \(XBY\) a \(XCZ\). Podľa nej (pre koeficient podobnosti) \(|XZ|:|XY| = |XC|:|XB|\). Keď si ich spojíme, dostaneme \(|XT|:|XE| = |XC|:|XB|\). V oboch pomeroch sú prvé strany z trojuholníka \(CXT\) a druhé z \(BXE\). Na podobnosť nám teda stačí, aby uhly medzi \(XT\) a \(XC\) a medzi \(XE\) a \(XB\) boli rovnaké.

To sme však už dopočítali, keď sme prvýkrát hovorili o daných trojuholníkoch. Zistili sme, že tieto uhly sú oba \(180^\circ - \delta\). Môžeme si teda všimnúť, že trojuholníky \(BXE\) a \(CXT\) sú podobné. Potom nutne \(|\sphericalangle XBT| = |\sphericalangle XCT|\), takže \(T\) leží na osi \(BC\), čo je skutočne os uhla \(\sphericalangle BAC\).

Bod \(X\) je v strede \(BC\)

V takomto prípade je \(X\) priamo na osi súmernosti trojuholníka \(ABC\). Vďaka \(|\sphericalangle BXY| = |\sphericalangle CXZ|\) je osovo súmerný aj trojuholník \(XYZ\) a teda \(YZ\) je kolmá na \(AX\). Rovnobežka s \(YZ\) je teda totožná s \(BC\), jej priesečník s \(XZ\) bude priamo \(X\). Stred \(X = T\) strany \(BC\) leží na osi uhla \(ABC\), keďže je to rovnoramenný trojuholník.

Bod \(X\) je bližšie k \(B\)

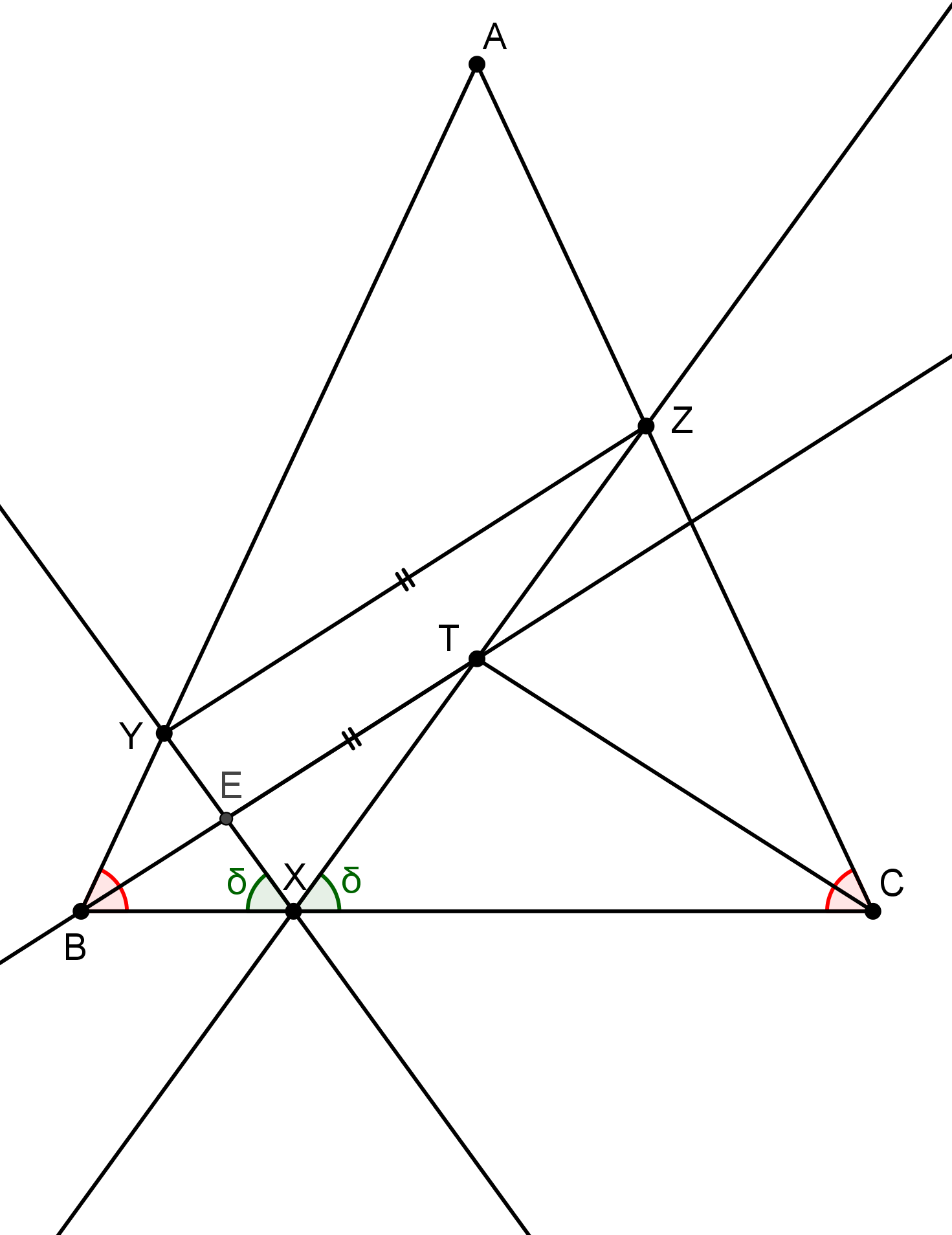
Na úvod si všimnime, že naše úvahy o trojuholníkoch \(XBY\) a \(XCZ\) prejdú rovnako aj v tejto konfigurácií. Tie sú teda podobné. Rovnako sa zachová aj podobnosť trojuholníkov \(XYZ\) a \(XTE\). Rovnobežnosť zo zadania sa nezmenila a tak máme aj rovnoľahlosť, len tentokrát s kladným koeficientom. Otázny je len osud trojuholníkov \(BXE\) a \(CXT\).

Podobne ako minule dostaneme z prvých dvoch podobností, že \(|XT|:|XE| = |XZ|:|XY| = |XC|:|XB|\). Potrebujeme už len uhol medzi \(XE\) a \(XB\) a medzi \(XT\) a \(XC\). To je však tentokrát o niečo jednoduchšie. Keďže \(E\) leží na polpriamke \(XY\), uhol \(\sphericalangle BXE\) je priamo \(\delta\). Analogicky \(|\sphericalangle CXT| = |\sphericalangle CXZ| = \delta\).

Opäť dostaneme podobnosť \(BXE\) a \(CXT\), takže \(|\sphericalangle XBT| = |\sphericalangle XCT|\) a \(T\) bude ležať na osi strany \(BC\) a teda aj uhla \(\sphericalangle BAC\).