Templár Slavomír, vracajúci sa zo zemí saracénskych domov, si nemohol nevšimnúť krivosť mestských stien. Ako povinnosť káže, ihneď o tom upovedomil svoju kráľovnú Kiku. Tú to tak vyviedlo z miery, až prikázala svojmu najlepšiemu architektovi Mirovi, aby hradby zdemoloval (v tom je on expert) a nahradil ich najnovším typom trojcípich hradieb stojacich na špeciálnej trojuholníkovej sieti.
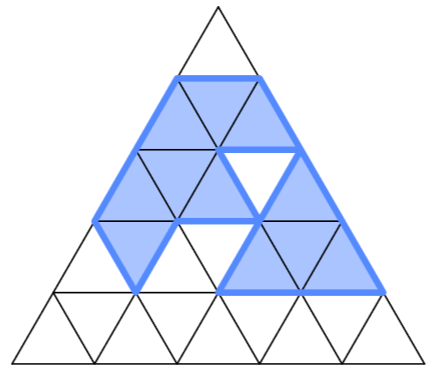
Rovnostranný trojuholník so stranou dĺžky \(n\) je rozdelený na \(n^2\) rovnostranných trojuholníkov so stranou dĺžky \(1\). Miro si vyberie niekoľko z týchto trojuholníkov tak, aby sa po stranách vybraných trojuholníkov dalo prejsť medzi ľubovoľnými dvoma z nich. Následne postaví hradby na úsečkách medzi vybranými a nevybranými trojuholníkmi a tiež medzi vybranými trojuholníkmi a obvodom veľkého trojuholníka. Koľko rôznych počtov trojuholníkov si môže vybrať, ak celková dĺžka hradieb musí byť presne \(3n\)? Na obrázku môžete vidieť príklad možného výberu trojuholníkov, ktorý vyhovuje podmienkam.
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.