Zadanie
Prvou formou umenia, ktorú ľudstvo kedy vytvorilo, boli graffity. Ak neveríte, stačí sa zamyslieť, čo sa nám zachovalo po pravekých ľuďoch. Neboli to žiadne symfónie, olejomaľby ani básne. Boli to čarbanice na čerstvo zateplených stenách jaskyne. Najznámejšia z tých, ktoré sa zachovali do dnešných dní, zobrazuje vypätý moment z lovu mamutov. Vyzerá nasledovne:
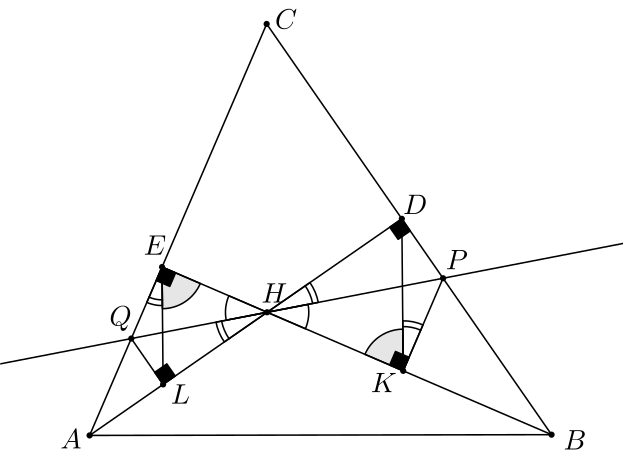
Základom je ostrouhlý trojuholník \(ABC\). Body \(D\) a \(E\) sú pätami výšok postupne na stranu \(BC\) a na stranu \(AC\). Priesečník priamok \(AD\) a \(BE\) je označený ako \(H\). Priamka cez bod \(H\) pretína úsečku \(BC\) v bode \(P\) a úsečku \(AC\) v bode \(Q\). Bod \(K\) leží na úsečke \(BE\) tak, že priamka \(PK\) je kolmá na \(BE\). Podobne, bod \(L\) leží na úsečke \(AD\) tak, že priamka \(QL\) je kolmá na \(AD\). Dokážte, že priamky \(DK\) a \(EL\) sú rovnobežné.
Na začiatok sa zamyslime, ako by sme vedeli dokázať rovnobežnosť dvoch priamok. Jedným zo základných spôsobov je hľadať zhodné súhlasné alebo striedavé uhly alebo tiež môžeme skúšať dokázať, že obe dané priamky sú kolmé na nejakú tretiu (toto je v podstate len špeciálny prípad). Samozrejme, existuje viacero ciest, ako vyriešiť túto úlohu. Pre začiatok si ukážeme to najzákladnejšie a potom spomenieme aj niekoľko ďalších.
Zo zadania poznáme pravé uhly \(HLQ\), \(HEQ\), \(HDP\) a \(HKP\). Ďalej si môžeme všimnúť, že bodom \(H\) prechádzajú až tri priamky, a teda tam máme mnoho dvojíc vrcholových uhlov, a tie sú zhodné. Z nich by mohli byť najzaujímavejšie dvojice \(|\sphericalangle LHQ|=|\sphericalangle DHP|\) a \(|\sphericalangle EHQ|=|\sphericalangle KHP|\), resp. aj \(|\sphericalangle LHE|=|\sphericalangle DHK|\) (to sú len súčty predchádzajúcich). Takže máme dve dvojice zhodných uhlov v trojuholníkoch \(HLQ\) a \(HDP\), a preto sú podobné. Z rovnakého dôvodu sú podobné aj trojuholníky \(HEQ\) a \(HKP\).
Môžeme si všimnúť, že koeficient podobnosti oboch dvojíc trojuholníkov je rovnaký, lebo majú spoločnú stranu (pre trojuholníky \(HLQ\) a \(HEQ\) je to strana \(HQ\), pre trojuholníky \(HDP\) a \(HKP\) strana \(HP\)). Preto sú aj celé štvoruholníky \(HEQL\) a \(HKPD\) podobné. Chceme ukázať, že uhlopriečka jedného je rovnobežná s uhlopriečkou druhého. Ako sme si už povedali, chceme to ukázať cez striedavé alebo súhlasné uhly. Vďaka podobnosti štvoruholníkov máme aj podobnosť trojuholníkov \(HEL\) a \(HKD\), a teda aj rovnosť veľkostí uhlov \(|\sphericalangle HEL|=|\sphericalangle HKD|\) a aj \(|\sphericalangle HLE|=|\sphericalangle HDK|\), čo sme chceli. Máme teda dvojicu zhodných striedavých uhlov (dokonca dve), vďaka čomu sú priamky \(EL\) a \(DK\) rovnobežné.
Iné riešenie
Vieme, že \(|\sphericalangle HDP | = |\sphericalangle PKH|= 90^\circ\). Potom \[|\sphericalangle HDP | + |\sphericalangle HKP| = |\sphericalangle DHK| + |\sphericalangle DPK| = 180 ^\circ.\]
To znamená, že body \(H,D,P,K\) tvoria tetivový štvoruholník. 1
Potom ale z vlastností obvodových uhlov \[|\sphericalangle DHP| = |\sphericalangle DKP|.\] Ďalej \[|\sphericalangle HKD| = 180 ^\circ - |\sphericalangle DKP| - |\sphericalangle PKB| = 90 ^\circ - |\sphericalangle DKP|.\]
Podobne \(|\sphericalangle HEQ | = |\sphericalangle QLH|= 90^\circ\), teda \[|\sphericalangle EQL | + |\sphericalangle EHL| = |\sphericalangle QLH| + |\sphericalangle QEH| = 180 ^\circ,\] a teda body \(E,Q,L,H\) tiež tvoria tetivový štvoruholník.
Z toho vieme \(|\sphericalangle QEL| = |\sphericalangle QHL|\), \[|\sphericalangle LEH| = 90 ^\circ - |\sphericalangle QEL| = 90^\circ - |\sphericalangle QHL|.\]
Vieme \(|\sphericalangle QHL| = |\sphericalangle DHP|\), a teda \[|\sphericalangle LEH| = 90 ^\circ - |\sphericalangle QEL| = 90^\circ - |\sphericalangle QHL| = 90^\circ - |\sphericalangle DHP|= 90^\circ - |\sphericalangle DKP| = |\sphericalangle HKD|.\]
Potom priamky \(EL, DK\) zvierajú rovnaký uhol s priamkou \(EK\), a teda sú rovnobežné.
Pre tých, čo ich nepoznajú: tetivový štvoruholník je špeciálny tým, že mu vieme opísať kružnicu. To sa dá práve vtedy, keď je súčet protiľahlých uhlov rovný \(180^\circ\).↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.