Zadanie
Každý môže súťažiť, no nie každý môže pracovať na poli. Tarzan so snúbenicou potrebovali okopať novovzniknuté pole, no prihlásilo sa im až priveľa algebraikov.
Pre pochybenie úradov má pole tvar štvorčekovej mriežky \(n \times n\), kde \(n\ge2\). Na niektorých políčkach sú algebraici, pričom žiadni dvaja nie sú na tom istom políčku. Každý algebraik kope motykou v jednom políčku, otočený jedným zo štyroch smerov rovnobežných so stranami poľa. Problémom je, že občas motyka vystrelí. Potom letí v smere, ktorým je algebraik otočený, až vyletí z poľa von alebo zasiahne iného algebraika. Koľko najviac algebraikov môžeme na pole umiestniť tak, aby s istotou nikto nebol zasiahnutý, keď motyka strelí? Umiestnením algebraika určujeme aj to, ktorým smerom bude otočený.
Rozdeľme si pole na rohové políčka (červené), krajné políčka (oranžové) a stredové políčka (zelené).
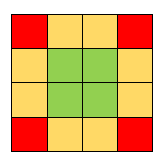
Uvažujme krajné políčka. Ak v nich je algebraik, môžeme ho bez ujmy na všeobecnosti otočiť smerom von z tabuľky. Teraz uvažujme stredové políčka. Pokiaľ by v takomto políčku mohol byť algebraik, ktorý je otočený zvisle a na nikoho nemieri, môžeme ho namiesto toho umiestniť na krajné políčko v tomto smere a nič tým nepokazíme. Pokiaľ by bolo toto políčko už obsadené, tento algebraik nemohol byť ani v stredovom políčku. Zároveň ho nikto nebude ohrozovať – ani v stĺpci, pretože to by ho ohrozoval už predtým, ani v riadku, pretože predtým sme otočili všetkých algebraikov na krajných políčkach smerom von.
Rovnako vieme presunúť algebraikov na stredových políčkach, ktorý sú otočení vodorovne, na krajné políčka v krajných dvoch stĺpcoch. Ľubovoľné rozmiestnenie spĺňajúce zadanie vieme takýmto spôsobom postupne upraviť tak, že sú všetci na obvode a nové rozmiestnenie stále spĺňa zadanie.
Takto vieme potupne umiestniť najviac \(2(n-2)\) algebraikov otočených zvisle na krajných políčkach a \(2(n-2)\) otočených vodorovne na krajných políčkach. To je spolu \(4n-8\) algebraikov. Jediné políčka, ktoré môžeme ešte obsadiť sú rohové, a tie sú \(4\). Algebraik na rohovom políčku môže mieriť ľubovoľným z dvoch smerov, smerom von z poľa. Spolu teda vieme umiestniť najviac \(4n-4\) algebraikov.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.