Zadanie

Milý denníček,
dnes za mnou prišiel exekútor, keďže som nemal dosť peňazí na zaplatenie dlhu. Normálne mi vošiel až do nory. Tak som ho zožral. Konečne viem, ako vyzerá šťastie.

Šťastie má tvar trojuholníka \(ABC\) so stredom opísanej kružnice \(O\). Bod \(T\) je na výške na stranu \(AB\) taký, že \(|\sphericalangle TBA| = |\sphericalangle ACB|\). Priamka \(CO\) pretína stranu \(AB\) v bode \(K\). Dokážte, že os strany \(AB\), výška na \(BC\) a úsečka \(KT\) sa pretínajú v jednom bode.

Označme si \(G\) priesečník priamky \(BT\) s osou strany \(AB\). Trojuholník \(ABG\) je rovnoramenný, preto platí \[|\sphericalangle AGB| = 180^\circ - 2|\sphericalangle TBA| = 180^\circ - 2|\sphericalangle ACB| = 180^\circ - |\sphericalangle AOB|.\] Keďže platí \(OG \perp AB\) a zároveň \(|\sphericalangle AGB| = 180^\circ - |\sphericalangle AOB|\), je \(G\) ortocentrum trojuholníka \(AOB\).

Nech \(H\) je ortocentrum trojuholníka \(ABC\). Označme \(E\) priesečník výšky \(AH\) s osou strany \(AB\), teda priamkou \(OG\). Stačí nám dokázať, že body \(K\), \(E\), \(T\) ležia na priamke.

Uvažujme kužeľosečku \(\mathcal{H}\) prechádzajúcu bodmi \(A\), \(B\), \(C\), \(H\), \(O\). Táto kužeľosečka je zjavne hyperbolou. Platí, že hyperbola prechádzajúca bodmi \(X\), \(Y\), \(Z\) je pravouhlá práve vtedy, keď na nej leží ortocentrum trojuholníka \(XYZ\).1 Keďže ortocentrum \(H\) leží na \(\mathcal{H}\) prechádzajúcej bodmi \(A\), \(B\), \(C\), je táto hyperbola pravouhlá. To znamená, že na nej leží aj ortocentrum trojuholníka \(AOB\), teda bod \(G\).

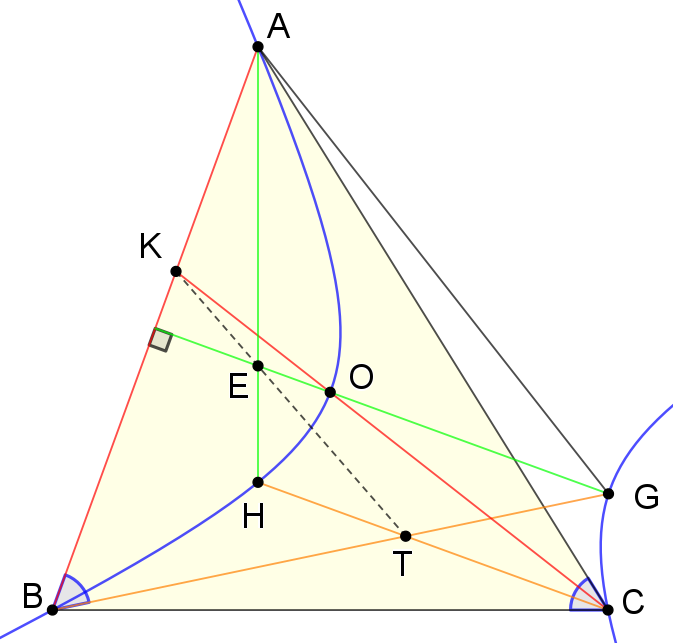
Keďže body \(A\), \(H\), \(C\), \(O\), \(G\), \(B\) ležia na \(\mathcal{H}\), môžeme použiť Pascalovu vetu2 na šesťuholník \(AHCOGB\) a tým dostávame, že \(AH\cap OG = E\), \(HC \cap GB = T\) a \(CO \cap AB = K\) ležia na priamke, čo sme chceli dokázať.

Poznámky

Žiadne z odovzdaných riešení nešlo podľa vzorového a ani jedno z nich nebolo syntetické.

  1. Ak nepoznáš, spoznaj tu https://davidaltizio.web.illinois.edu/geom-conics.pdf (Theorem 4.4).↩︎

  2. Ak nepoznáš, spoznaj tu https://en.wikipedia.org/wiki/Pascal%27s_theorem.↩︎

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.